Понятие текстовой задачи по математике
В повседневной жизни люди постоянно сталкиваются с термином «задача» как на профессиональном, так и на бытовом уровне. Нам зачастую приходится решать те или иные проблемы, которые мы привыкли называть задачами. Проблема решения задач, математических и которые возникают перед человеком в бытовой или производственной деятельности, начали изучаться с давних пор, но на сегодняшний день нет общепринятого толкования самого понятия «задача». В общепринятом понимании под задачей имеется в виду некоторая ситуация, требующая исследования и необходимого решения человеком.
Определения текстовой задачи предлагают различные авторы:
1.Текстовая задача – есть описание некоторой ситуации на естественном языке с требованием дать количественную характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между её компонентами или определить вид этого отношения (А.П. Тонких).
2. Текстовая задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий» (М.И.Моро и А.М. Пышкало).
Самого такового определения текстовой задачи нет, есть только понятие причем, по словам Н.В.Метельского это понятие есть неопределенным. По его мнению, «задача – понятие неопределяемое и в самом широком смысле слова означает то, что требует исполнения, решения. Иногда под задачей понимают упражнение, которое выполняется, решается посредством умозаключения, вычисления и т.п. Последнее толкование термина «задача» ближе к понятию «задача в обучении», которую можно назвать дидактической задачей. Математическая задача в обучении … является также неопределяемым понятием, подчиненным понятию «дидактическая задача»».
Существуют некоторые виды задач, которые выделяет Т.Е. Демидов:
1)Коллективные и групповые задачи,
2)Задачи общегосударственные,
3) Задачи определенного круга людей.
Если глубоко рассмотреть текстовую задачу, то можно понять что это некая ситуация которая требует определенного решения.
Задача как цель, которая заданная в определённых условиях, так А.Н. Леонтьев определяет понятие текстовой задачи. Л.Л. Гурова определяет текстовую задачу как объект, мыслительной деятельности, который требует практических действий или ответа на теоретический вопрос путем нахождения условий, необходимых для нахождения связей между неизвестными и известными её элементами. А Л.М. Фридман находит связь между понятием «задача» и «проблемная ситуация».
А.А. Темербекова выделяет математические задачи как особый вид, она в своих работах их раскрывает следующим образом. Математическая задача — это некий лаконический рассказ, в котором присутствуют значения некоторых величин и необходимо отыскать неизвестные значения величин, зависимые от данных и имеют связь в определённых соотношениях, которые даны в условии.
Правильно будет выделить отдельный блок математических текстовых задач, для которых необходимо знать особые математические знания.
Демидова Т.Е. делит задачи на два блока:
1)научные (например, проблема Гольбаха, теорема Ферма и т.д.), при решении развевается математика и её приложения. Они характеризуют настоящие предметы (масса, длина, скорость и т.д.).
2)учебные задачи — это задачи, которые направлены для формирования математических навыков, знаний и умений в разных категориях обещающихся и направлены для улучшения личности обучаемого. А объекты в этих задачах математические (фигуры, числа, и т.д.).
Математическая задача – это необходимость реализовать некоторую математическую деятельность, для которых условие уже указано.
По роли, которую играют учебные задачи, их, делят на:
1)репродуктивные (для решения такого вида задач необходимо знать
определённую формулу),
2)задачи с известным алгоритмом (это такой вид задач, для решения
которых необходимо проделать определённую последовательность действий, для
достижения результата),
3)проблемные (это задачи, которые ориентируют учащихся, на решение какой либо проблемы, связанной с содержанием текста или определено речевым действием, которое необходимо выполнить или обратить внимание).
Задачи, в которых все объекты математические (вычислительные задания,
доказательство теорем и т.д.) принято называть математическими задачами.
Математические задачи называются текстовыми, если в них присутствует хотя бы один объект, который является реальным предметом.
Важнейшая особенность текстовых задач заключается в том, что в них не показывается, открыто, какое собственно действие необходимо выполнить для получения ответа на вопрос задачи.
В любой текстовой задаче можно выделить следующее:
1)Числовые значения, которые принято называть известными или данными (их следует быть не менее двух),
2)Некоторую систему функциональных зависимостей в неявном виде, взаимоотношения данных и искомых и данных между собой,
3)Вопрос или требование, на который нужно найти ответ.
Условие задачи называют числовые значения величин и имеющиеся между ними некие связи, то есть качественные и количественные характеристики предметов задачи и взаимоотношений между ними. В задаче, как правило, не одно условие, а несколько, которые называют элементарными. Вопрос в задаче может быть выражен как в повествовательной, так и в вопросительной форме, и их также как условий, может быть несколько. Значение величин, которые необходимо найти называют искомой величиной, а числовые величины искомых значений, называют неизвестными или искомыми.
Для того чтобы получить ответ на требование задачи, для этого необходимо ее решить. Решить задачу это значить найти взаимоотношения между данными, которые даны в условии задачи, и искомыми величинами, установить последовательность применение общих положений математики (формул, законов, правил, и так далее), выполнить определенные действия которые даны в задаче, применяя общее положение и получить ответ на требование задачи или доказать что его нет.
Виды задач в курсе математики начальной школы
Виды задач в курсе математики начальной школы
Существует несколько классификаций видов задач в математике.
Виды задач классифицируют по содержанию, сюда входят следующие виды задач:
вычислительные;
задачи на доказательство;
задачи на построение;
комбинированные задачи.
Особое место при изучении задач занимает такой вид, как текстовые задачи, которые можно подразделить на традиционные и нетрадиционные (проблемные). Традиционные текстовые задачи – это задачи на движение, работу и т.д. Проблемные текстовые задачи – это и есть нестандартные задачи.
Виды задач классифицируют по функциям:
дидактические;
развивающие;
познавательные;
контролирующие задачи.
Функции задач можно определить как глобально, так и локально. Вышеперечисленные функции являются глобальными. Локальные функции учитываются при подготовке к конкретному уроку. Дидактические задачи предусматривают и используют на этапе закрепления. Познавательные задачи несут в себе то новое, что предусматривается в целях обучения на данном этапе. Развивающие задачи – это новые незнакомые проблемные задачи.
Виды задач классифицируют по обучающей роли в изучении школьного курса:
задачи на усвоение;
задачи на овладение математической символикой;
задачи на обучение доказательству;
задачи на формирование математических умений и навыков;
задачи развивающего характера.
В зависимости от числа известных ученику компонентов выделяют следующие виды задач:
тренировочные упражнения (шаблонные задачи), в них известны и цель, и способ решения, и ответ. К первому виду задач относят учебные задачи, где известны цель и условие задачи, они занимают наибольшее содержание учебника;
нестандартные задачи – в таких задачах известно только условие;
задачи-проблемы – известна только цель. Данные задачи встречаются в быту и производстве, где четко определена только цель, необходимые условия пути и средства решения ученик должен определить самостоятельно.
Задача, для решения которой надо выполнить несколько действий, связанных между собой, называется составной задачей.
Составная задача включает в себя ряд простых задач, связанных между собой так, что искомые одних простых задач служат данными других.
В процессе обучения математике в начальной школе учащиеся решают как простые, так и составные задачи. Приведем виды и примеры задач, изучаемых в курсе начальной школы, основанных на классификации, предлагаемой О.Н. Горуновой .
Простые задачи I группы (при решении данных задач усваивается конкретный смысл каждого из арифметических действий):
Нахождение суммы двух чисел.
Нахождение остатка.
Нахождение суммы одинаковых слагаемых (произведения).
Деление на равные части.
Деление по содержанию.
Простые задачи II группы (при решении этих задач усваивается связь между компонентами и результатами арифметических действий; к ним относятся задачи на нахождение неизвестных компонентов):
Нахождение первого слагаемого по известным сумме и второму слагаемому.
Нахождение второго слагаемого по известным сумме и первому слагаемому.
Нахождение уменьшаемого по известным вычитаемому и разности.
Нахождение вычитаемого по известным уменьшаемому и разности.
Нахождение первого множителя по известным произведению и второму множителю.
Нахождение второго множителя по известным произведению и первому множителю.
Нахождение делимого по известным делителю и частному.
Нахождение делителя по известным делимому и частному.
Простые задачи III группы (при решении этих задач раскрываются понятия разностного отношения; к ним относятся простые задачи, связанные с понятием разностного отношения):
Разностное сравнение чисел или нахождение разности двух чисел.
Увеличение числа на несколько единиц (прямая форма, косвенная форма).
Уменьшение числа на несколько единиц (прямая форма, косвенная форма).
Простые задачи IV группы (при решении этих задач раскрываются понятия кратного отношения; к ним относятся простые задачи, связанные с понятием кратного отношения):
Кратное сравнение чисел или нахождение кратного отношения двух чисел. (Во сколько раз больше? Во сколько раз меньше?).
2) Увеличение числа в несколько раз (прямая форма, косвенная форма).
3) Уменьшение числа в несколько раз (прямая форма, косвенная форма).
Из этих простых задач можно составить разнообразные составные задачи в 2, 3, 4 и более действий.
Рассмотрим примеры простых задач.
Задачи на нахождение суммы:
«На ветке сидело 4 воробья и 3 снегиря. Сколько птиц сидело на ветке?».
Задачи на увеличение и уменьшение числа на несколько единиц:
«В Северном Ледовитом океане 10 морей, а в Индийском на 5 меньше. Сколько морей в Индийском океане?».
«Антон нашел 5 боровиков, а сыроежек на 4 больше. Сколько сыроежек нашел Антон?».
Задачи на нахождение неизвестного слагаемого:
«За два дня турист прошел 8 км. В первый день он прошел 3 км. Сколько км он прошел во второй день?».
Задачи на нахождение остатка:
«На дереве сидело 7 птиц. 3 улетели. Сколько птиц осталось?».
Задачи на нахождение неизвестного вычитаемого и слагаемого:
«У Иры было 9 тетрадей. Когда несколько тетрадей Ира исписала, их осталось — 6. Сколько тетрадей исписала Ира?».
«На полке было 5 книг. Когда еще несколько книг поставили на полку, их стало 8. Сколько книг поставили на полку?».
Задачи на нахождение уменьшаемого:
«Когда Коля раскрасил в книжке 4 картинки, их осталось 3. Сколько картинок в книжке?».
Задачи на разностное сравнение:
«В саду 8 кустов малины и 5 кустов крыжовника. На сколько больше кустов малины, чем кустов крыжовника? На сколько меньше кустов крыжовника, чем кустов малины?».
Задачи с косвенными вопросами:
«Ров первого деревянного кремля имел глубину 5 м, что на 2 м больше, чем его ширина. Какова ширина рва?».
«Жук олень имеет длину 7 см, что на 4 см меньше длины уссурийского усача. Какова длина уссурийского усача?».
Простые задачи на умножение:
«Сколько колес у 3 двух колесных велосипедов?».
Задачи на увеличение и уменьшение числа в несколько раз:
«У Сережи 4 солдатика, а у Антона в 2 раза больше. Сколько солдатиков у Антона?».
«В кружках занималось 18 мальчиков, а девочек в 2 раза меньше. Сколько девочек занималось в кружке?».
Задачи на деление по содержанию и на равные части:
«У плотника 16 дощечек. Сколько скворечников можно сделать из этих дощечек, если на один скворечник идет 8 дощечек?».
«Тесьму длиной 3 м разрезали на 3 одинаковые части. Сколько метров тесьмы в каждой части?».
Задачи на кратное сравнение:
«В бидоне 10 л молока, а в кувшине 5 л. Во сколько раз меньше молока в кувшине, чем в бидоне. Во сколько раз больше молока в бидоне, чем в кувшине?».
Задачи на увеличение и уменьшение числа в несколько раз (косвенная форма):
«На одной стороне улицы 24 дома. Это в 3 раза больше, чем на другой. Сколько домов на другой стороне?».
«В саду росло 18 черешен. Это в 3 раза меньше, чем персиковых деревьев. Сколько персиковых деревьев в саду?».
Теперь приведем примеры составных задач, составленных из этих простых задач.
Составные задачи на нахождение суммы:
«В магазин привезли 20 ящиков конфет, а печенья на 6 ящиков больше. Сколько всего ящиков привезли в магазин?».
«На Земле 4 океана, а материков на 2 больше. Сколько всего океанов и материков на Земле?».
«На полке стояло 9 книг на немецком языке, а на английском на 14 книг больше, чем на немецком, а на французском языке на 12 книг меньше, чем на английском. Сколько всего книг стояло на полке?».
Составные задачи на нахождение остатка:
«В классе учились 12 девочек и 10 мальчиков. Потом 4 человека ушли. Сколько человек осталось?».
Составные задачи на нахождение слагаемого и вычитаемого.
«В классе 14 девочек и 15мальчиков. В школу пришло 18 детей. Сколько детей заболело?».
«Ежик собрал 28 яблок. 9 из них он отдал ежику и еще несколько белочке. Сколько ежик отдал яблок белочке, если у него осталось 12 яблок?».
Составные задачи на нахождение третьего слагаемого:
«У нашей кошки 11 котят: 3белых4 черных и несколько рыжих. Сколько рыжих котят у нашей кошки?».
Составные задачи на нахождение уменьшаемого:
«В банке были соленые огурцы. За завтраком съели 12 огурцов, а в обед 21. Сколько огурцов было в банке, если в ней осталось 15 огурцов?».
Составные задачи на разностное сравнение:
«В тетради 6 чистых страниц, исписано на 4 страницы больше. На сколько меньше исписанных страниц, чем всего страниц в тетради?».
«В коробке было 9 красных и зеленых ручек. Из них красных — 3 ручки. На сколько больше было зеленых ручек, чем красных?».
Составные задачи на нахождение суммы и кратное сравнение:
«Мама купила 12 кг земляники, что в 4 раза больше, чем малины. Сколько килограммов ягод купила мама?».
Составление задачи на нахождение уменьшаемого, вычитаемого, разности:
«Для уроков труда купили 4 набора цветной бумаги по 10 листов в каждом наборе. На поделки истратили 36 листов. Сколько листов осталось?».
«Бабушка засолила несколько банок помидоров по 5 кг в каждой банке. Зимой съели 30 кг и осталось 10 кг помидоров. Сколько помидоров засолила бабушка?».
«На пришкольном участке ребята вырастили морковь. После того, как разложили морковь в 2 корзины, по 6 кг в каждую — осталось 28 кг. Сколько килограммов моркови вырастили ребята?».
Составные задачи на разностное и кратное сравнение:
«6 ящиков с банками весят 30 кг, а ящик с хурмой 4 кг. На сколько легче ящик с хурмой?».
«6 ящиков киви весят 18 кг, и 2 ящика манго 12 кг. Во сколько раз ящик с манго весит больше, чем ящик с киви?».
Задачи на нахождение суммы двух произведений:
«Школьники окопали 2 ряда яблонь по 6 деревьев в каждом ряду и 3 ряда вишен но 5деревьев в каждом ряду. Сколько всего фруктовых деревьев окопали школьники?».
Задачи на нахождение неизвестного слагаемого:
«Для детского сада купили 68 кг конфет. Карамель лежала в 6 коробках по 4 кг в каждой, а шоколадные конфеты в 4 коробках. Сколько килограммов шоколадных конфет в каждой коробке?».
Задачи на приведение к единице:
«Для 6 гирлянд надо 12 фонариков. Сколько потребуется фонариков для 2 гирлянд?».
Составные задачи на деление суммы на число:
«С одной грядки сняли 18 кг репы, а с другой 54 кг. Всю репу разложили в корзины по 9 кг в каждую. Сколько потребовалось корзин?».
Кроме этого, в курсе начальной школе рассматривают особые виды задач, связанных с пропорциональными величинами и элементами геометрии.
Простые задачи на цену, количество, стоимость:
«5 пуговиц стоят 350тенге. Сколько стоит одна пуговица?».
«У Коли 4 монеты по 50 тенге. Сколько денег у мальчика?».
«Батон хлеба стоит 100 тенге. Сколько батонов хлеба можно купить на 300 тенге?»
Составные задачи на цену, количество, стоимость.
«Для школы купили 5 линеек по 80тенге и столько же карандашей по 20тенге. Сколько денег заплатили?».
«За 6 м шелка и 3 м шерсти заплатили 4200тенге. Метр шерсти стоит 600 тенге. Сколько стоит метр шелка?».
«Миша купил на 180 тенге 6 конвертов. Сколько конвертов он купит на 60тенге?».
Задачи на нахождение периметра и сторон геометрических фигур:
«Сторона прямоугольника а = 5 см, а b на 2 см короче. Чему равен периметр прямоугольника?».
«Сторона прямоугольника а = 4 см, Р = 14см. Чему равна сторона b?».
Простые задачи на движение:
«Расстояние от города до поселка 30 км. Сколько времени потребуется пешеходу. Чтобы пройти это расстояние со скоростью 6 км/ч?».
«Мальчик пробежал 20 м за 10 секунд. С какой скоростью бежал мальчик?».
«Муха летела со скоростью 5 м/с 15 секунд. Какое расстояние она пролетела?».
Задачи на встречное движение.
«Два мальчика одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 200 м. Они встретились через 20 секунд. Первый бежал со скоростью 5 м/с. С какой скоростью бежал второй мальчик?».
«Расстояние между селами 48 км. Через сколько часов встретятся два пешехода, которые вышли одновременны навстречу друг другу, если скорость одного 3 км/ч, а другого 5 км/ч?».
«Из двух городов одновременно навстречу друг другу выехали 2 автобуса. Скорость первого автобуса 25 км/ч, скорость второго 50 км/ч. Первый автобус прошел до встречи 100 км. Сколько км прошел до встречи второй автобус?».
Задачи на движение в одном направлении:
«Лыжник шел со скоростью 18 км/ч и был в пути 3 часа. Сколько времени потребуется пешеходу, чтобы пройти такое же расстояние, если его скорость9км час?».
«Отряд прошел 39 км. Первые 3 часа он шел со скоростью 5 км/ч. Остальную часть пути отряд прошел за 6 часов. С какой скоростью отряд прошел остальную часть пути?».
Задачи на противоположное движение и движение в обратном направлении:
«Из гаража одновременно в противоположных направлениях вышли две автомашины. Одна шла со скоростью 50 км/ч, а другая со скоростью 70 км/ч. На каком расстоянии друг от друга будут эти машины через 4 часа?».
«Из одного поселка вышли в одно и то же время в противоположных направлениях два пешехода. Скорость одного 5 м/ч, а скорость другого 6 км/ч. Через сколько часов расстояние между ними будет равно 33 км?».
«От пристани одновременно в противоположных направлениях отошли два теплохода. Через 6 часов расстояние между ними было 360 км. Один из них шел со скоростью 28 км/ч. С какой скоростью шел другой теплоход?».
Задачи на нахождение четвертого пропорционального:
«За 5 дней израсходовали 10 кг овощей. Сколько килограммов овощей израсходовали за 3 дня, если каждый день расходовали овощей поровну?».
Задачи на пропорциональное деление:
«Двое рабочих заработали 200000тенге. Один работал — 2 недели, а другой 8недель. Сколько денег заработал каждый?».
Задачи на нахождение неизвестного по двум разностям:
«В одном куске было 6 м ткани, а в другом 12 м такой же ткани. Второй кусок стоит на 2400тенге дороже, чем первый. Сколько стоил каждый кусок ткани?».
Задачи на совместную работу:
«Малыш может съесть 600г варенья за 6 минут, а Карлсон – в 2 раза быстрее. За какое время они съедят это варенье вместе?».
Задачи на нахождение числа по доле и доли по числу:
«Какой длины потребуется проволока для прямоугольной рамки, если длина рамки 25 см, а ширина равна 4/5 длины?».
«2/5 кружки сахарного песку весит 100 г. Сколько весит кружка сахарного песку?».
Задачи на нахождение площади, периметра:
«Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?».
«Площадь витрины квадратной формы 64 м². Узнай ее периметр».
«Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?».
Мы привели примеры задач, рассматриваемых в курсе начальной школы. Но, если говоря о простых задачах, можно ограничиться несколькими группами, то говоря о составных задачах, можно сказать, что это далеко не полный перечень возможных задач.
Таким образом, составные задачи отличаются очень большим разнообразием, поэтому нельзя говорить о формировании навыка решения составных задач, т.к. их решение не может быть автоматическим. При решении каждой составной задачи необходимо проводить ее полный анализ, исследование, для того, чтобы ответить на вопрос. Поэтому решение составных задач вызывает у учащихся наибольшие затруднения.
Литература:
Горунова О. Н. Классификация и виды задач в начальной школе [Электронный ресурс]. – Режим доступа: https://infourok.ru/klassifikaciya-i-vidi-zadach-v-nachalnoy-shkole-1112462.html – Загл. с экрана. – Яз.рус.]
Математика «Что такое задача»
КСП по математике в 1 классе
3 четверть 27 урок
*В контексте тем:«Путешествие», «Традиции и фольклор»
Школа:
Дата: «____»____________20___г.
ФИО учителя:
Класс: 1 «____» класс.
Количество присутствующих:
отсутствующих:
Тема урока:
Что такое задача
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
подбирать опорную схему для решения задачи.
Цели урока:
Познакомить учащихся с понятием задача и ее составными частями — условием и вопросом; научить оформлять решение и ответ к задаче.
Критерии успеха
Термин «задача» в начальной школе используется в значении «текст, описывающий жизненную ситуацию, с использованием численных характеристик».
Привитие
ценностей
Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Межпредметные
связи
Межпредметные связи содержат перечень ссылок на другие предметы, которые имеют отношение к уроку. Разнообразные виды заданий выполняются на уроке с целью осуществления интеграции с другими предметами. Например, задачи обучения в рамках конкретного урока по предмету «Математика» можно рассмотреть через такие предметы, как «Естествознание» и «Художественный труд».
Навыки
использования
ИКТ
На данном уроке учащиеся не используют ИКТ. Возможный уровень:
организованная деятельность, включающая презентации и ИKT;
самостоятельное изучение информации, обсуждение в группе; представление классу полученных выводов;
Предварительные
знания
Уравнения всех изученных типов с вычислениями в пределах 20 и десятками до 100. Умение выбрать нужный способ решения из трех возможных. Комментирование решения уравнений на основе взаимосвязи между частью и целым по алгоритму.
Ход урока
Этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
Вводное задание. Начните урок с проведения исследовательской работы — поиска ответа на вопрос: «Что такое задача?».
Критерии успеха
Запишите на доске предмет исследования — слово ЗАДАЧА.
Середина урока
Предложите учащимся подумать и обсудить в группах, что такое задача. Выслушайте их ответы. В помощь детям раздайте опорные таблицы.
7 + 3Чему равно значение суммы?
Жанар прочитала 7 книг о животных и 3 книги о путешествиях. Сколько книг прочитала Жанар?
Задайте вопросы:
Чем похожи эти задания? Чем они отличаются?
Каким способом можно выполнить каждое задание?
Какое из этих двух заданий будет задачей? Выслушайте ответы учащихся. Выясните, почему
они так думают. Сообщите, что задача — это математическое высказывание. В тексте задачи обязательно содержатся условие и вопрос.
Предложите школьникам определить в тексте условие и вопрос задачи. Проведите обсуждение в виде фронтальной работы. Прочитайте условие задачи и вопрос. Обсудите, в чем их отличие. Закрепите новые понятия, записав их на доске или при помощи табличек со словами: УСЛОВИЕ и ВОПРОС.
Переходя к следующему этапу, спросите, как ответить на вопрос задачи. Выслушайте предположения учащихся. Резюмируйте, что для ответа на вопрос задачу нужно решить. Запишите на доске слово РЕШЕНИЕ.
Попросите детей сделать предположение. Спросите, что получается в результате решения задачи. Обобщите ответы учащихся, сообщив, что в результате решения задачи находят ОТВЕТ. Запишите термин на доске.
С помощью схемы можно изобразить все компоненты задачи, увидеть их взаимосвязь и найти неизвестный компонент. Например: Жанар прочитала 7 книг о животных и 3 книги о путешествиях. Сколько всего книг прочитала Жанар?
1. Что означает первая часть схемы? (Количество книг о животных.)
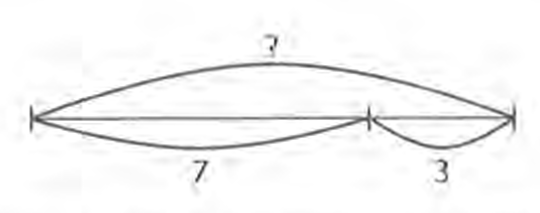
А вторая часть? (Количество книг о путешествиях.)
Что нужно узнать в задаче? (Сумму прочитанных книг.)
Объясните, как следует построить схему к задаче. Поясните, что при наличии визуальных данных задачу легче решить.
Задача. Прочитав вместе с учащимися условие задачи, организуйте выполнение формирующего задания. Выпишите основные шаги, необходимые для решения задачи:
прочитай задачу;
определи, что известно и что неизвестно в задаче;
подбери схему к задаче или составь краткую запись;
определи ход решения;
запиши решение задачи;
запиши ответ.
Выполнение упражнений в учебнике закрепляет знания об основных частях задачи.
Реши. Предложите учащимся прочитать задачу. Спросите, какие из основных четырех частей задачи они могут выделить в тексте. Прежде чем дети приступят к решению задачи, помогите им ее проанализировать. Дайте соответствующие рекомендации:
Этап понимания содержания задачи: «Прочитай текст задачи, определи о чем или о ком идет речь».
Этап планирования: «Рассмотри рисунок или схему к задаче. Определи части и целое. Объясни, что обозначает каждое число».
Этап решения: «Подумай, как ответить на вопрос задачи. Какое действие следует совершить, чтобы найти неизвестное целое? Запиши решение задачи».
Этап проверки: «Запиши ответ к задаче. С помощью обратного действия сделай проверку», Опираясь на данный алгоритм, реши задачу.
Учебник:
Что такое задача, с. 58—59. Рабочая тетрадь:
Рабочий лист 53, «Что такое задача», с 55. Рабочий лист 54, «Части задачи», с. 56.
Ресурсы:
названия составных частей задачи: «Условие», «Вопрос», «Решение», «Ответ», написанные на отдельных карточках;
схемы для составления и решения задач;
памятки с названиями частей задачи;
текст заданий на листах бумаги.
Критерии успеха
Ответ
14 + 3 = 17 (пр.)
Ответ: 17 предметов.
Конец урока
Попробуй. Задание направлено на закрепление понимания взаимосвязи между вопросом и текстом задачи. Опираясь на иллюстрацию, учащиеся составляют условие задачи. В ходе работы следует обращать их внимание на памятку, в которой перечислены все составляющие части задачи
Критерии успеха
Дифференциация
Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание
Как Вы планируете проверить уровень усвоения материала учащимися?
Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
Здоровье и соблюдение техники безопасности
Здоровьесберегающие технологии.
Используемые физминутки и активные виды деятельности.
Дополнительные задания
Составь задачу. Учащиеся соотносят части задачи с соответствующими названиями, проводя линии, соединяющие воздушные шары и корзины.
Они записывают ответ в числовое выражение (решение задачи), а полученное число — в ответ.
Ответ
Условие «Путешественник 15 часов ехал на автобусе и 4 часа шел пешком».
Вопрос: «Сколько часов путешественник был в пути?»
Решение: схема и числовое выражение: 15 + 4 = 19 (ч)
Ответ: 19 часов.
Пройди лабиринт. Первоклассники соотносят части задачи с их названиями, проходя дорожки лабиринта.
Чтобы выяснить, на каком уровне учащиеся овладели знаниями по данной теме, задайте следующие вопросы:
Назовите основные части задачи, (Условие, вопрос, решение, ответ.)
Что такое вопрос задачи?
Если в тексте отсутствует вопрос, будет ли это задачей?
Проведите работу с учащимися по самооцениванию с помощью «Лестницы успеха» в рабочей тетради.
Физкультминутка.
Чтоб все выполнить заданья,
Всем нам надо отдохнуть,
Ну, ребята, дружно встанем,
Надо косточки встряхнуть.
Руки вверх, назад прогнулись,
Сейчас сделаем наклоны,
К упражнению готовы?
Раз, два, три, четыре, пять.
Теперь спинки держим ровно.
На месте будем мы шагать.
Раз, два, три, четыре, пять.
Тихо все на место сядем
И закроем глазки,
Вспомните всё, что сегодня узнали,
Без моей подсказки.
Урок математики «Что такое задача» (1 класс)
Краткосрочный план урока математики № 1-3-27
В контексте тем:«Путешествие», «Традиции и фольклор»
Школа: филиал ОАНО «СШ «ЦО Столичный»
ФИО учителя: Грицюк Ирина Валентиновна
Класс: 1 «А»
Тема урока: «Что такое задача»
Цели обучения, которые достигаются на данном уроке:
1.5.1.1. Моделировать задачу в виде схемы, рисунка, краткой записи; подбирать опорную схему для решения задачи.
Задачи урока:
Познакомить учащихся с понятием задача и ее составными частями — условием, вопросом, решением и ответом.
Научить определять части задачи.
Критерии успеха
(Предполагаемый результат)
Все учащиеся будут:
понимать значение термина «задача»; распознавать в тексте задачи условие и вопрос; отличать задачу от другого текста.
Термин «задача» в начальной школе используется в значении «текст, описывающий жизненную ситуацию, с использованием численных характеристик»
Многие учащиеся будут:
соотносить части задачи с термином; выбирать нужное арифметическое действие для решения.
Некоторые учащиеся будут:
составлять задачу по картинке, находить ее решение из трех предложенных.
Привитие ценностей
Ценности, основанные на национальной идее «Мәңгілік ел»: сотрудничество; уважение к партнеру; труд и творчество; открытость во взаимодействии; образование в течение всей жизни.
Межпредметные связи
Естествознание. Темы «Животные», «Времена года»
Навыки использования ИКТ
На данном уроке учащиеся не используют ИКТ.
Организованная учебная деятельность включает мультимедийную презентацию.
Коллаборативная среда
Самостоятельное изучение информации через обсуждение в группе.
Предварительные знания
Навыки сложения и вычитания в пределах 10.
Умение выбрать нужный способ решения из трех возможных.
Языковая цель
Овладение математической терминологией: задача, условие, вопрос, решение, ответ. Включение данных терминов в активный словарный запас.
ХОД УРОКАЭтапы урока
Запланированная деятельность на уроке
ресурсы
Начало урока
«Внешний и внутренний круг»
Психологический настрой на работу через поиск качеств, необходимых для успешной работы на уроке. Деление на пары.
ромашка-подсказка
Вводное задание.
Отгадывание ребусов.
-Что такое сложение и вычитание?
Решение примеров и получение результата – слово ЗАДАЧА
Проведение исследовательской работы — поиска ответа на вопрос: «Что такое задача?»
На доске термин предмета исследования — слово ЗАДАЧА, которое нужно составить, расположив значения выражений в порядке убывания.
А
Ч
А
А
З
Д
демонстрационные карточки с ребусами
слайд презентации
Середина урока
Исследовательская работа в парах:
-Что такое задача?
Обсуждение в группе. Афиширование результатов обсуждения.
Сравните тексты.
Обсудите с партнером
— Какой из текстов можно поместить в учебник «Математика», а какой в книгу для чтения? Почему?
У утки вылупилось 9 утят. Они с удовольствием плескались в речке. Плавали от берега к берегу.По речке плавало 9 утят. 3 утенка выбрались на берег. Сколько утят осталось плавать в речке?
Определение понятия «задача»
Задача – это математическое высказывание. В тексте задачи всегда содержится условие и вопрос.
5к.
?к.
3к.
карточка с картинкой и текстами для каждой пары
Физ
минутка
Вышли мыши как-то раз
Посмотреть, который час.
Раз, два, три, четыре.
Дернули за гири!
Тут раздался страшный звон.
Побежали мыши вон!
Объединение в группы.

Работа в группе.
Составление и решение задачи. Определение частей задачи.
Ответ: __ птичек
5 – 2
3 + 2
5 — 3
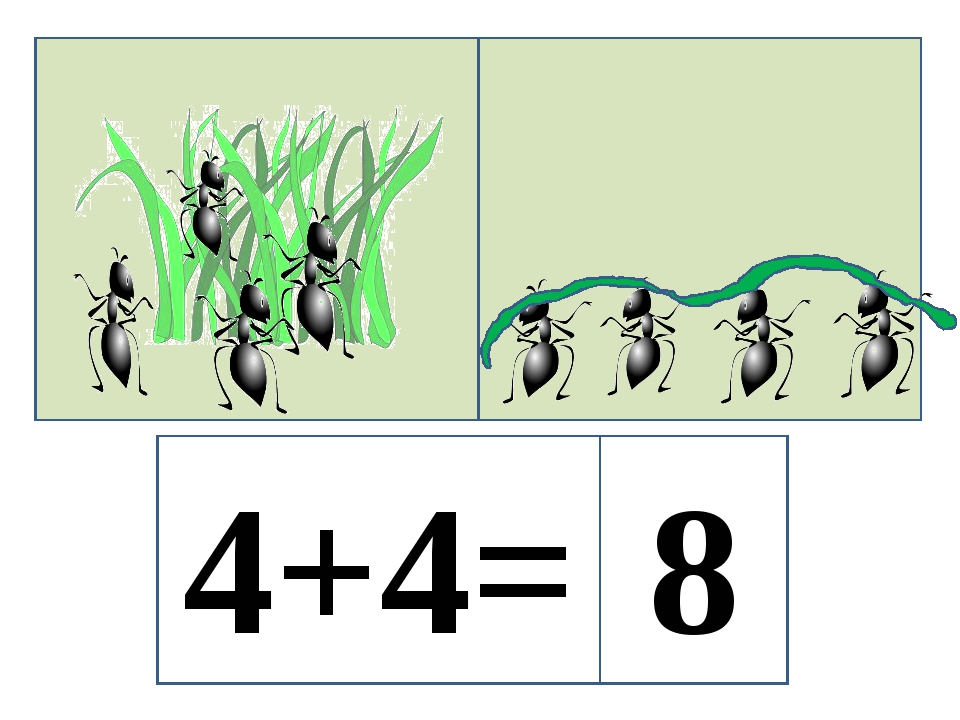
На ветке сидели 3 птички. Прилетели еще 2 птички. Сколько птичек стало?
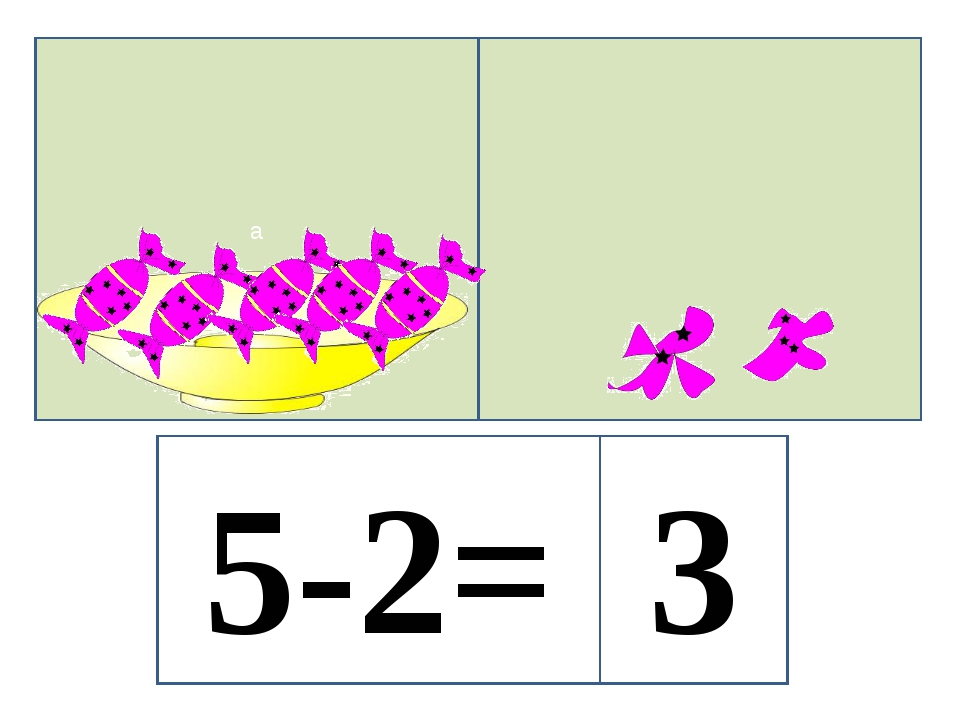
На ветке сидели 5 птичек. 2 птички улетели. Сколько птичек осталось?
Выбор действия для решения задачи. Обоснование.
Соотнесение частей задачи с текстом. Устно.

карточка
для каждой группы
слайд презентации
Формативное оценивание
Самостоятельная работа. Взаимооценивание.
Соотнести части задачи с названием.
ВОПРОССколько цветов в двух вазах?
РЕШЕНИЕ
В одной вазе 5 цветов, а в другой 4 цветка.
ОТВЕТ
УСЛОВИЕ
индивиду
альные карточки
«Фишбоун»
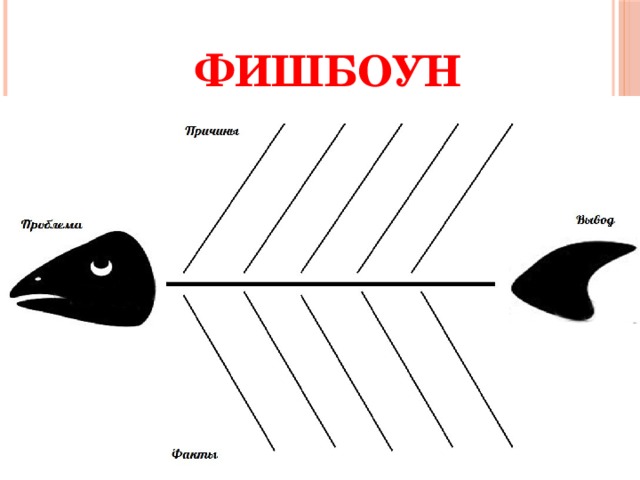
Расположить части задачи и термины на скелете, соотнеся друг с другом.
Дети выходят к доске и прикрепляют карточки на нужное место.
демонстрационный плакат с карточками
Конец урока
Попробуй. Задание направлено на закрепление понимания взаимосвязи между вопросом и текстом задачи. Опираясь на иллюстрацию, учащиеся составляют условие задачи.
В ходе работы дети опираются на памятку, в которой перечислены все составляющие части задачи


Самопроверка.
слайд презентации
карточка-эталон для самопроверки
Форматив
ное оценивание
Учебная беседа:
(Условие, вопрос, решение, ответ.)
Что такое вопрос задачи?
что содержит условие задачи?
Без чего не может быть задачи?
Рефлексия
Самооценивание.
«Лестница успеха»
модель лестницы на доске
Урок математики в 1 классе «Что такое задача?» (УМК Л.В.Занков)

 Урок математики в 1 классе (УМК Л.В.Занкова)
Урок математики в 1 классе (УМК Л.В.Занкова)
Тема: Что такое «задача».
Цель: ученик усвоит понятие «задача», научиться выделять части задачи.
Задачи:
создание условий для ознакомления с понятием «задача», «части задачи»;
обеспечение первичного усвоения знаний на уровне применения их в разнообразных ситуациях;
развитие логико-математической речи, внимания, аналитического мышления, формирование умения выделять части и решать задачи;
воспитание интереса к предмету, дисциплинированности.
Формирование универсальных учебных действий:
1. Регулятивные УУД:
— формулировать тему и цель урока с помощью учителя;
— учиться высказывать своё предположение на основе работы материала учебника;
— определять успешность выполнения задания в диалоге с учителем.
2. Познавательные УУД:
— наблюдать и делать выводы.
3. Коммуникативные УУД:
— слушать и понимать речь своих товарищей, умение работать в парах, группе, вести диалог.
4. Личностные УУД:
— формирование положительной учебной мотивации, навыков самооценки, понимание смысла учебной деятельности.
Технологии:
Технология деятельностного метода,
Технология личностно — ориентированного обучения
Игровая, здоровьесберегающая технология
Тип урока: открытие нового знания
Оборудование: учебник «Математика», 1 класс, 2-я часть. Авторы И.И.Аргинская, Е.П.Бененсон, Л.С.Итина. Самара: Издательство «Учебная литература»: Издательский дом «Федоров». 2013; интерактивная доска, цифровой диск, карточки с названиями этапов исследования, карточки со снеговиками и снегурочками, веера цифр у детей, карточки с названиями составных частей задачи, тексты задач.
Ход урока:
-У нас на уроке гости, давайте поздороваемся!
I. Орг. момент. Мотивация к учебной деятельности.
Я рада, что вы собрались здесь, друзья.
И думаю, встретились мы не зря.
Мы будем учиться сегодня решать,
Исследовать, сравнивать и рассуждать,
Секрет математики вновь открывать.
– Сегодня на уроке мы будем внимательно слушать учителя и друг друга, наблюдать, стараться запоминать и понимать.
Девиз нашего урока: «Знаешь – говори, не знаешь – слушай».
И так, друзья, в путь! Но для начала, как всегда, нужна гимнастика ума. (1-2 мин.)
II . Устный счет.
1. Вопросы
— Сколько хвостиков у 4 щенят?
— Назовите второй день недели.
— Сколько месяцев длится лето?
— Что лишнее: ручка, карандаш, отрезок?
— Чего больше на лугу: цветов или ромашек?
— Что общего у снега и одеяла?
2. Местоположение чисел
-Возьмите веера цифр.
— Покажите «соседей» чисел 5, 7, 9, 6, 2.
3. Задачи в стихах
Перед тем, как приступить к изучению новой темы, нужно себя настроить на математический лад. Приготовьте ваши веера.
а) На забор взлетел петух
Повстречал еще там двух.
Сколько стало петухов? (3)
б) Три цыпленка стоят
На скорлупки глядят.
Два яичка в гнезде
У наседки лежат.
Сосчитай поверней,
Отвечай поскорей:
Сколько будет цыплят
У наседки моей? (5)
в) 6 орешков мама-свинка
Для детей несла в корзинке.
Свинку ежик повстречал
И еще 4 дал.
Сколько орехов свинка
Деткам принесла в корзинке? (10)
4. Повторение таблицы сложения в пределах 10.
Игра на интерактивной доске (онлайн – тренажер – пазл -сайт learningapps)
(10-12 мин) (приложение 2)
(Индивидуальное задание для детей с ОВЗ) (приложение 1)
III. Подготовка к работе на основном этапе.
1.Подведение к целеполаганию.
На доске ребус (за слогом да идет слог ча) Ответ ЗАДАЧА
— Ребята, а что такое задача? Как вы понимаете это слово?
— Как оно относится к математике? Хотите узнать?
— Кто может сформулировать цель нашего урока сегодня?
(узнать что такое ЗАДАЧА, и как это слово связано с математикой). (2-3 мин.)
2. Актуализация знаний. (Работа в парах)
У вас на партах есть листочки с картинками.
Составьте математический рассказ к картинке со снегурочками. (приложение 3)
А теперь составьте математический рассказ к картинке со снеговиками. (приложение 4)
Чем отличаются ваши рассказы?
( в одном рассказе есть вопрос, а в другом нет).
Вот один из ваших рассказов называется задача, как вы думаете какой?
(про снеговиков)
Докажите своё мнение.
Так какой вывод вы можете сделать?
(ЗАДАЧА – это математический рассказ, в котором есть вопросительное предложение? (вопрос) (5-6 мин)
Цифровая физкультминутка (1 мин.)
IV. Открытие нового знания
— Юные мои математики, не хотите ли узнать ещё что-то о задаче? Или мы уже всё знаем и можно начинать новую тему? Я открою вам секрет: у задачи есть составные части! Хотите узнать, что это за части? С этой целью предлагаю провести исследование по теме. В конце урока мы должны получить проект под названием «Задача».
— Давайте наметим наш план действий. ( На доске) (1 мин.)
1. План действий
1 этап — карточка с восклицательным знаком (надпись «Подумать!»)
2 этап — «Узнать из книг или из других источников » (рисунок книги)
3 этап — «Наблюдение и эксперимент» (рисунок ладони)
4 этап — «Обобщение материала» (нарисован вопросительный знак) (приложение)
— Все этапы понятны? Желаю удачи! Я предлагаю вам разделиться на две группы по три человека
1 этап — карточка с восклицательным знаком (надпись «Подумать!») (1 мин.)
2. Работа с каточками
I этап
— я вам раздам карточки, а вы должны выбрать, что относится к нашей теме задача и расположить в определенном порядке: условие, вопрос, решение, ответ, задача, самолет, нитка (приложение 5)
Группы вывешивают на доске свои варианты и доказывают свою точку зрения.
(затем на доске остается правильный вариант дети сверяют, оценивают)
Работа с учебником
Откройте учебник на с. 36. №88.
— Выбери из трех текстов задачу.
— Обсудите свой выбор.
В задаче то, что нам известно, называется УСЛОВИЕМ. А то, что нужно найти — ВОПРОСОМ задачи. Прочитайте в нашей задаче условие. А теперь вопрос задачи. (На листочках — УСЛОВИЕ, ВОПРОС). (8 мин.)
— Давайте проверим это знание на втором этапе.
2 этап
— Узнать из книг или другого источника (рисунок книги)
— Из какой книги вы сейчас можете узнать о задаче? (из словаря или интернета).
Дети с помощью учителя ищут определение термина «ЗАДАЧА» в интернете.
— Итак, действительно, задача состоит из УСЛОВИЯ, ВОПРОСА.
На доске текст задачи.
На дереве сидело пять ворон.
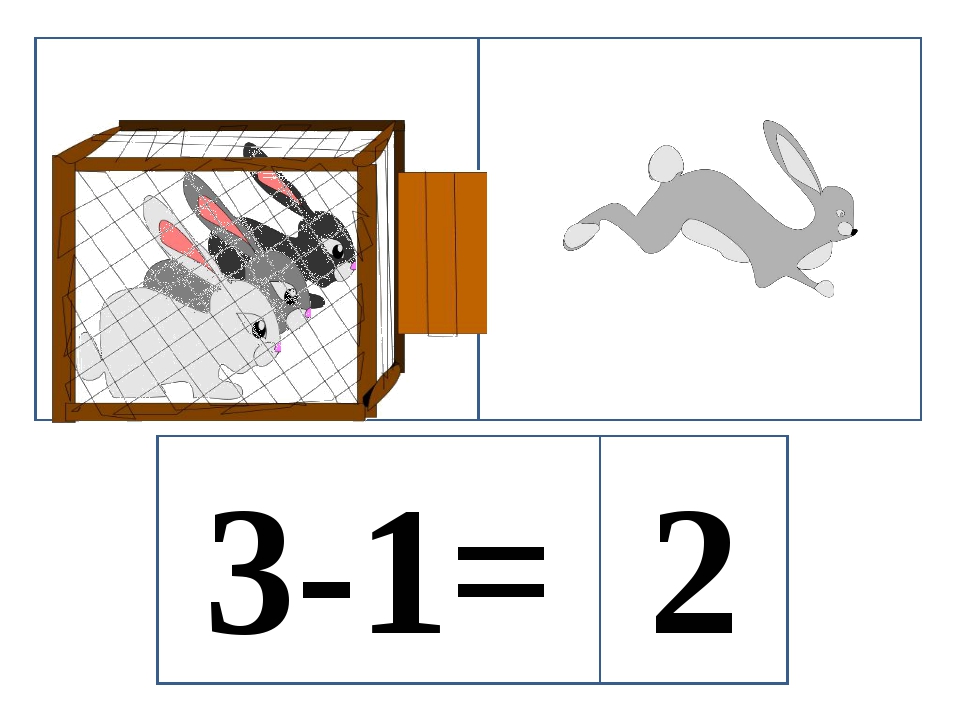
Одна ворона улетела.
Сколько ворон осталось?
Подчеркните синими чернилами условие задачи, а красными – вопрос задачи. (4-5 мин.)
3 этап
— «Наблюдение и эксперимент» (рисунок ладони)
— Вернемся к нашим полузадачам с. 36 №88 и проанализируем их: а можем ли мы им помочь превратиться в настоящие задачи? Каких частей не хватает?(ответы детей) — Давайте решим их. (решают устно)
4 этап
— «Обобщение материала» (нарисован вопросительный знак)
На доске записаны слова столбиком: ЗАДАЧА, УСЛОВИЕ, ВОПРОС, РЕШЕНИЕ, ОТВЕТ
-Кто ответит на вопрос: Что такое задача? Каковы составные части задачи? В каком порядке они располагаются?
— Если условие неполное, не хватает чисел — можно решить задачу?
— Если нет вопроса, можно ли считать такую запись задачей?
— Посмотрите на доску. Весь собранный материал у нас расположен в строгой последовательности. Это и есть наш проект, который мы должны были составить к концу урока
-Мы справились с этим заданием?
Задача состоит из условия, вопроса. Задачу можно решить и дать ответ на вопрос. (5 мин.)
V. Закрепление нового материала.
— Мы с вами так много говорили о задачах и я предлагаю вам решить несколько интересных задач. В этом мне поможет пингвиненок Вилли.
Задачи от пингвиненка (говорящая игрушка). (3-5 мин.)
VI. Систематизация и самооценка полученных знаний.
— Какие новые знания вы получили на уроке? .
VII. Итог урока. Рефлексия учебной деятельности.
— Какие умения помогли вам сегодня на уроке?
— Какие знания вы использовали и приобрели?
— Как одним понятием назвать математический рассказ? (задача)
— Из чего состоит задача? (Условие, вопрос)
Рефлексия:
Я узнал …
Я научился…
Мне понравилось…
Я бы хотел… (1-2 мин)
Приложение 1
Расставь цифры в порядке возрастания.
5 3 7 9 2 8 1 6 4
Восстанови натуральный ряд чисел.
… 2 3 … 5 … 7 8 …
Реши равенства.
1+1= 2+2= 3+4=
2+1= 2+3= 3+5=
3+1= 3+2= 3+3=
4+1= 4+2= 3+6=
5+1= 5+2= 4+3=
Приложение 2
Приложение 3

Приложение 4

Приложение 5
Приложение 6

План-конспект урока по математике (1 класс) по теме: «Что такое задача». (сценарий урока)
Урок математики в 1 классе «Что такое задача».
(Система Л.В.Занкова, ФГОС).
Васильева Людмила Николаевна,
Васильева Людмила Николаевна,
учитель начальных классов,
МОУ Лицея №15, г. Саратова.
МОУ Лицея №15, г. Саратова. учитель начальных к МОУ Лицея №15, г. Саратова.
Автор учебника: И.И.Аргинская, Е.П.Бененсон, Л.С.Итина, С.Н.Кормишина
Тип урока: урок «открытия» новых знаний
Тема урока: «Что такое задача».
Деятельностная цель: формирование у учащихся умений реализации новых способов действия.
Содержательная цель: расширение понятийной базы за счёт включения в неё новых элементов.
Задачи урока:
Предметные
- формировать умение устанавливать различия между задачей и математическим рассказом;
- составлять числовые выражения на увеличение/уменьшение чисел.
Личностные
Формировать способность к самооценке на основе критерия успешности учебной деятельности; развитие этических чувств, доброжелательности и эмоционально-нравственной отзывчивости.
Метапредметные
Регулятивные: формировать умение определять и формулировать цель на уроке с помощью учителя, работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение.
Коммуникативные
Формировать умение планировать учебное сотрудничество с учителем и сверстниками; с достаточной полнотой и точностью выражать свои мысли; находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Познавательные:
Общеучебные: умение структурировать знания, осознанно и произвольно строить речевое высказывание, самостоятельно формулировать познавательную цель, рефлексия способов и условий действия.
Логические: формировать умение анализировать объекты с целью выделения признаков, формулировать проблему; самостоятельное создание способов решения проблем творческого и поискового характера.
Методы обучения: проблемный, поисковый, исследовательский.
Вид деятельности: продуктивная деятельность.
Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.
Средства обучения: учебник, мультимедийный проектор, презентация, карточки трёх видов.
Ход урока:
1.Самоопределение к деятельности
Организационный момент (2 мин)
Цель: выработка на личностно-значимом уровне внутренней готовности выполнения нормативных требований учебной деятельности.
Начинается урок.
Он пойдёт ребятам впрок.
Постарайтесь всё понять,
Учитесь тайны открывать.
Ответы полные давайте
И на уроке не зевайте.
На доске пословица: «Век живи – век учись».
— Как понимаете эту пословицу?
-Значит, чему будет посвящён урок? (открытию новых знаний).
— А чтобы узнать о чём пойдёт речь, вам придётся найти значение этих выражений.
4+2=д 8-6=ч 4+5=з
3-3=а 5-1=а 3+4=а
(ответы записаны на перевёрнутых листочках, с обратной стороны которых записаны буквы.
— Расположите ответы в порядке убывания (9,7,6,4,2,0). Переверните карточки. Что получилось? (Задача).
-Что такое задача хотите узнать? (да)
2. Актуализация знаний и фиксация затруднений в пробном действии (10 мин)
Цель: подготовка мышления учащихся и организация осознания ими внутренней потребности к построению нового способа действий.
Перед вами 4 истории:
1. Сколько морковок было у зайчика?
2. Зайчик уронил 1 морковку.
3. Зайчик уронил 1 морковку. У него осталась ещё 5. Всего у него было 6 морковок.
4. Зайчик уронил 1 морковку. У него осталась ещё 5. Сколько морковок было у зайчика сначала?
— Какая история будет являться задачей? (разные ответы детей).
— Почему мы не можем точно ответить на вопрос? Чего мы не знаем?
( Не знаем что такое задача).
3. Выявление места и причины затруднения.
(Постановка учебной задачи). (2 мин)
Цель: Осознание того, в чём именно состоит недостаточность знаний, умений, способностей учащихся; постановка цели урока.
— В каком месте возникло затруднение? (при выборе задачи).
— Почему возникло затруднение? (не знаем, что такое задача).
— Какую цель ставим? (Узнать, что такое задача. Из каких частей состоит. Чем отличается от обычной истории).
— Сформулируйте тему урока? ( «Что такое задача»).
4. Построение проекта выхода из затруднения. (3 мин)
Цель: выбор способа и средств его реализации.
Наметим план действий:
— Сами попробуем узнать, что такое задача. Выскажем свои предположения.
— Сопоставим свои предположения с учебником или спросим у учителя.
— Устраним затруднения.
— Применим новые знания.
— Что нам поможет? (Свой опыт, учебник, учитель).
— Предположите, что такое задача?
— Где мы можем уточнить? (обратимся к словарю).
(В толковом словаре С.И.Ожегова задача – это «то, что требует решения»). Для того чтобы дать ответ, что должно быть в задаче? (вопрос).
Вывод 1: В задаче должен быть вопрос.
5. Реализация построенного проекта. (8 мин)
Цель: построение учащимися нового способа действий и формирование умений его применять.
– Прочитайте следующую запись. (Чего больше яблок или вишен?)
Это задача? (Нет).
— Почему? Ведь это вопрос? (Нам ничего не известно.
-Значит в задаче должно быть то, что известно, т.е. условие.
Вывод 2. В задаче должен быть вопрос и условие.
— Прочитайте следующую запись. (В вазе 5 яблок и 4 груши. На сколько вишен больше, чем бананов?)
— Это задача? (нет). – Почему? Есть и условие и вопрос? (Они не связаны по смыслу).
Вывод: условие и вопрос в задаче связаны по смыслу.
Физминутка
Вернёмся к нашим историям и попробуем снова.
-Какая же история является задачей? (4-ая). — Почему?
Вывод 3: В любой задаче есть вопрос и условие, которые связаны по смыслу.
— Что нужно сделать, чтобы ответить на вопрос задачи? (решить её)
— А чтобы решить, надо её проанализировать, понять. А поможет рисунок. Составим выражение. Запишем его. Назовём ответ.
6. Первичное закрепление. (7 мин)
Цель: усвоение учащимися нового способа действия.
С.34 № 84.
-Составь математический рассказ по первым трём рисункам.
(«В кормушке было 5 воробьёв. К ним прилетели ещё 3 воробья. Теперь в кормушке 8 воробьёв»).
— А по второй серии картинок? (В кормушке было 5 снегирей. Потом прилетели ещё 3 снегиря. Сколько снегирей стало?»).
_ Чем отличаются тексты? (разные птицы и последним предложением).
— Какой же текст является задачей? (второй) Докажите. (Условие и вопрос связаны по смыслу).
Решим её. 5+3=8(с).
Ответ: 8 снегирей.
7. Самостоятельная работа с самопроверкой по эталону (7 мин)
Цель: интериоризация нового способа действия и исполнительская рефлексия достижения цели пробного учебного действия.
Самостоятельно № 84 (2) Составляют задачу по рисунку. Записывают решение.
Самопроверка по эталону.
«Было 3 снеговика. Один растаял. Сколько снеговиков осталось?
3-1=2 (с.)
Ответ: 2 снеговика.
8. Включение в систему знаний и повторения. (3 мин)
Цель: повторение и закрепление ранее изученного и подготовка к изучению следующих разделов курса.
Работа в парах. № 87. Логическая задача. Проверка.
(Задание на запись выражений и нахождение их значений).
— У меня в руке три конверта. Вы вправе сами выбрать задание. Красный – сложнее, жёлтый – легче, а зелёный – работаю пока с учителем и классом.
Класс № 86 на доске с учеником и учителем, остальные решают самостоятельно, затем самопроверка.
9. Рефлексия учебной деятельности (итог урока) (3 мин)
Цель: самооценка учащимися результатов своей учебной деятельности.
— Какая тема урока была?
— Какую цель ставили? Достигли цели?
Расскажите по схеме чему научились на уроке.
-Я узнал…
— Я научился…
— Мне понравилось…
— Я бы хотел…
— Новые знания мне пригодятся…
— Оцените свою деятельность на уроке, используя один из кружочков: зелёный, красный, жёлтый.
Обратные задачи / Задачи / Справочник по математике для начальной школы
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
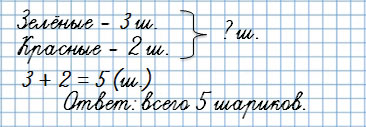
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
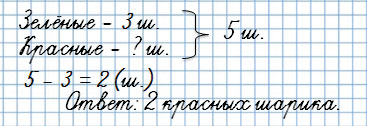
Ты видишь, что известная величина — красные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
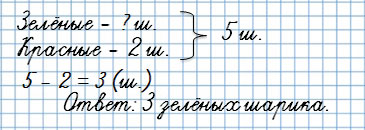
Ты видишь, что известная величина — зелёные шарики — стала неизвестной.
А неизвестная величина — общее количество шариков — стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
2 класс
Страница 26, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 57, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 72, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 83, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 85, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Задание 19, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 8. Вариант 1. № 3, Моро, Волкова, Проверочные работы
Страница 17. Вариант 2. № 1, Моро, Волкова, Проверочные работы
Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 14, Моро, Волкова, Рабочая тетрадь, 2 часть
3 класс
Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 19, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 20, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 27, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 38, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 32, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 30, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 71, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 6, Моро, Волкова, Рабочая тетрадь, 2 часть
4 класс
Страница 5, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 11, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 76, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 87, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 1 часть
Страница 49, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 68, Моро, Волкова, Рабочая тетрадь, 1 часть
Страница 28, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 32, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 44, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, 2 часть
Страница 29, Моро, Волкова, Рабочая тетрадь, 2 часть
© budu5.com, 2020
Пользовательское соглашение
Copyright
