Как научиться устному счету: Как научиться быстро считать в уме любые числа: техники устного счета

Содержание

Как научиться быстро считать в уме любые числа: техники устного счета

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

Карл Фридрих Гаусс

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить

4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Таблица умножения

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить

528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим

32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

79*50=(70+9)*50=3500+450=3950
79*7=(70+9)*7=490+63=553
3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число

75.

Раньше все считали без калькуляторов

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8

будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

Не забывайте тренироваться каждый день;
не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

«Самый быстрый способ научиться устному счёту» Узорова Ольга Васильевна, Нефедова Елена Алексеевна — описание книги | Самый быстрый способ:Узорова

Алтайский край

Альметьевск

Амурская область

Ангарск

Астрахань

Белгород

Богучар

Братск

Брянск

Владивосток

Владимирская область

Волгоград

Воронеж

Воронежская область

Екатеринбург

Ивановская область

Иркутск

Кабардино-Балкарская Республика

Калужская

Кемерово

Кемеровская область

Киров

Краснодарский край

Красноярск

Красноярский край

Курганская

Курск

Липецк

Лиски

Москва

Московская область

Нижнеудинск

Нижний Новгород

Нижний Тагил

Нововоронеж

Новосибирск

Омск

Оренбург

Оренбургская область

Орловская область

Пенза

Пермь

Поворино

Республика Адыгея

Республика Башкортостан

Республика Крым

Республика Северная Осетия — Алания

Республика Татарстан

Республика Хакасия

Россошь

Ростов-на-Дону

Ростовская область

Рязань

Самара

Саратов

Саянск

Севастополь

Смоленск

Ставрополь

Ставропольский край

Старый Оскол

Тамбов

Томск

Тула

Тюмень

Улан‑Удэ

Усолье‑Сибирское

Усть‑Илимск

Хабаровск

Ханты-Мансийский автономный округ

Челябинск

Челябинская область

Чита

Чувашская Республика

Шелехов

Энгельс

Ямало-Ненецкий автономный округ

Ярославль

Что такое устный счет? Хитрости, которые помогут вам считать без калькулятора

Вот как улучшить свое умение считать, которое поможет избавиться от калькулятора.

Вы хорошо считаете? Даже если ваш ответ будет утвердительным, в любом случае вам, как и всем, хочется научиться считать без калькулятора еще быстрей и лучше. Знаете ли вы, что каждый из вас может научиться считать без калькулятора?

Нет, мы ведем речь не о том, что вы сможете высчитывать тригонометрию в уме. Давайте поговорим об обычных вычислениях, которые можно быстро делать в уме , без использования смартфона или калькулятора.

Что такое математика в уме – устный счет?

Устный счет – это умение с помощью математики проводить вычисления в своей голове. К сожалению, хорошо считать в уме могут не все. Но это не означает, что устному счету нельзя научиться. Нет, это, конечно, не означает, что вы, если вам не дано, сможете почти мгновенно вычислить в уме, сколько будет 8974387 x 396. Но в какой-то мере вы все же можете улучшить свои навыки устного счета. Так что же такое математика в уме ?

Как мы уже сказали, устный счет – это вычисления без калькулятора и использования бумаги . Весь устный счет происходит в вашей голове. Чтобы научиться хорошо считать в уме, необходимо развивать в себе этот навык и постоянно тренироваться. Увы, без тренировок вы вряд ли сможете удивить кого-то своим умением считать большие числа в уме.

Полезен ли устный счет?

Наш ответ – однозначно да. Развивая свой навык математического счета в уме, вы развиваете свой мозг, свою память и логику. А научившись хорошо считать в уме, вы вдобавок станете более остроумным. Но главное – вы избавитесь от вашей зависимости считать даже маленькие числа на калькуляторе. Согласитесь, разве вам не приятно поймать себя на мысли, когда вы будете тянуться к калькулятору: «Подожди, мне это не нужно!» и далее найти ответ в своей голове?

К счастью, помимо развития подобного навыка за счет постоянных тренингов, существуют некоторые математические приемы, которые ускоряют и упрощают ваши вычисления в уме. Но также помните, что некоторые математические задачи все-таки было бы глупо не решать с помощью калькулятора. Так что все зависит от того, что именно вы хотите посчитать.

Смотрите также

Как научиться быстрее считать в уме, а также считать большие числа?

Многие из нас с ростом популярности смартфонов, наверное, уже не раз ловили себя на том, что у нас тянется рука к телефону, чтобы включить приложение «Калькулятор» для того, чтобы сложить или умножить простейшие небольшие цифры. Причем это происходит даже в том случае, если вы спокойно можете сделать вычисления в уме. Увы, многие современные технологии хоть и упростили нам жизнь, во многом нас уже давно обленили.

Пример вам – навигатор в смартфонах, из-за которого многие из нас уже разучились пользоваться бумажными картами местности. То же самое происходит и с математическим счетом в уме. Мы ленимся считать даже маленькие цифры, используя элементарные правила математики. Советуем вам отказаться от постоянного счета на смартфоне и использовать для вычислений свою память.

Боитесь, что у вас это не получится? Не переживайте. Если вы действительно хотите узнать, как научиться хорошо считать в уме, вам нужно знать некоторые приемы, упрощающие счет, и, конечно же, постоянная практика. Например, вы можете купить 20-гранный кубик с числами и, бросая его, перемножать числа в уме, проверяя правильный ответ на калькуляторе. Также в Сети есть множество примеров для тренировки устного счета. А теперь поговорим о математических трюках, которые помогут вам ускорить и упростить вычисления в уме.

Смотрите также

Примеры умственных математических трюков

В дополнение к практике умственного счета вы также можете усовершенствовать свое умение считать в уме, используя несколько простых и полезных математических трюков, которые работают для определенных типов задач. Например, если вы умножаете число на 9, вам не нужно беспокоиться о запоминании запутанных таблиц. Вместо этого просто умножьте число на 10, а затем вычтите число, которое вы умножили на 10, из полученного результата. Так вы гораздо проще получите ответ при умножении какого-либо числа на 9. Правда, намного проще? Например, мы хотим умножить число 53 на 9. Вместо этого в уме проще провести следующие вычисления:

53 х 10 = 530
530 — 53 = 477
Проверяем: 53 х 9 = 477

Смотрите также

Вот еще один интересный и очень полезный математический прием: чтобы, например, удвоить число (особенно если оно большое), нет нужды делать вычисление столбиком на бумажке; для этого просто удвойте каждый из отдельных «компонентов числа», а затем сложите их. Причем сделать это будет проще, если вы разобьете большое число на составные. Допустим, мы хотим удвоить число 329.

Для этого разбейте его на 300 + 20 + 9. Удвойте каждое из этих чисел, получив 600, 40 и 18, – намного проще, чем удвоить все число! Затем вы можете сложить все вместе, чтобы получить 658. И это лишь один из многих математических трюков, которые заметно упрощают счет в уме.

Методика быстрого счета без калькулятора

Цифры окружают нас с детства. Еще до школы или в первом классе человек учится складывать и вычитать, решать простые примеры и задачи. Позже он осваивает таблицу умножения, переходя к более сложной части математических упражнений. Большинство людей может производить в уме только простые вычисления. А вот умножение и деление больших значений приходится выполнять на бумаге или с помощью калькулятора. Но можно ли как-то научиться хорошо считать без использования подручных средств?

Быстрый счет без калькулятора

Жизнь любого современного человека неотрывно связана с числами. Без умения считать невозможно выполнять самые простые повседневные задачи. Конечно, сегодня у людей появились умные помощники – калькуляторы, смартфоны, компьютеры, но даже они могут иногда подвести – сломаться или не вовремя разрядиться. Да и не всегда можно полагаться на гаджеты, ведь на экзаменах в школе или в ВУЗе они не помогут. Именно поэтому многие люди стремятся научиться хорошо считать без помощи подручных средств. Особенно это актуально для школьников, ведь если с детства освоить техники быстрого устного счета, то и учеба в школе, и различные задачи во взрослой жизни будут даваться легче.

Есть еще одна серьезная причина для того, чтобы начать тренироваться хорошо считать в уме. Устный счет развивает человеческий мозг и способствует росту уровня интеллекта. Поэтому даже те студенты, которые обучаются на гуманитарных специальностях, все равно изучают такие точные науки, как высшая математика и математический анализ. Упражнения, направленные на устный счет больших чисел, являются отличной зарядкой для ума. Так развитие интеллекта и удобство в быту – это две самые главные причины научиться хорошо считать без калькулятора.

Человечество еще с древности стремилось найти такие способы быстрого счета. И речь не только о простых вычислениях, таких как сложение и вычитание, но и о более сложных – об умножении и делении. Пусть это и занимает много времени, но складывать и вычитать большие значения все же можно без предварительной подготовки, а вот такие действия, как умножение двузначных чисел, недоступны большинству людей.

Но, благодаря труду математиков со всего земного шара, сегодня появились некоторые математические хитрости, позволяющие считать в уме не только однозначные, но и двузначные числа. Чтобы понять принцип их работы, лучше рассмотреть каждый из этих приемов отдельно.

Как научить ребенка считать в уме

Ментальная арифметика – это далеко не новая система быстрого счета, ведь она зародилась еще в древности, около пяти тысяч лет назад. С тех пор данная методика не претерпела серьезных изменений и дошла до нас в практически первозданном виде. В ее основе лежат вычисления на абакусе – специальных счётах. Сначала человек учится решать простейшие примеры на них, а затем постепенно переходит к более сложному этапу обучения – учится представлять абакус в уме и производить вычисления на нем в своем воображении.

Лучше всего ментальная арифметика подходит именно детям. Нет, взрослые также могут ее освоить, но для этого им придется абстрагироваться от привычных методов операций с числами, а ребенок справляется с этим намного легче. Для него ментальная арифметика является не только помощником на уроках математики, но и способом развить свои интеллектуальные способности до очень высокого уровня.

Весь секрет этой методики в том, что она подразумевает разностороннее развитие человека. За логику и анализ отвечает правое полушарие мозга, именно оно задействуется на обычных уроках математики, когда мы решаем примеры или задачи. Правое полушарие, отвечающее за креативное мышление и фантазию, в этом случае к работе почти не подключается, а значит и не развивается должным образом. А ведь все области человеческого интеллекта необходимо тренировать.

Так как ментальная арифметика задействует и аналитическое мышление, и воображение, она является даже не столько способом быстро решать математические задачи, сколько средством для всестороннего развития. Другие методики чаще всего направлены на тренировку какой-то одной способности, а данная техника работает комплексно. Именно это выделяет ее среди прочих и делает одной из самых популярных систем развития интеллекта ребенка.

Обучение ментальной арифметике занимает достаточно много времени, но те преимущества, которые она дает, оправдывают затраченные усилия. Когда речь идет об обучении ребенка по данной методике, важно подобрать правильную программу тренировок. Ключевым фактором успеха является соблюдение плана занятий и контроль их регулярности. Несмотря на то, что в открытых источниках в интернете можно найти много информации по этому запросу, не всегда удается самостоятельно освоить ментальную арифметику. Поэтому большинство родителей предпочитают обучать ребенка этой технике в детских центрах дополнительного образования.

Как выбрать эффективную методику

Сегодня многие учебные заведения предлагают пройти курсы ментальной арифметики. Но детское образование – это очень сложный и многогранный процесс, поэтому родители должны походить к нему внимательно, и выбирать такие занятия, которые точно принесут пользу.

Выбирая школу ментальной арифметики, обращайте внимание на то, чтобы обучение велось по проверенной методике и учитывало возрастные особенности каждого ребенка. Нельзя, чтобы в одной группе обучались дети из начальной школы и старшеклассники, ведь в каждом возрасте своя скорость освоения, запоминания и закрепления материала.

К тому же, маленьким детям лучше всего преподавать любой предмет в игровой форме. Так они не будут уставать учиться и смогут сохранять концентрацию в течение всего урока. Внедрение игры в образовательный процесс способствует повышению интереса ребенка к математике.

Очень важно, чтобы тренер успевал уделить внимание каждому ученику в процессе занятия, но это возможно только в небольших группах. Поэтому стоит отдавать предпочтение тем детским центрам, где педагог обучает не более десяти детей единовременно. Только тогда удастся заниматься с максимальной продуктивностью.

Если учебный план организован правильно, то ребенку удастся приобрести полезные навыки, благодаря которым математика станет для него интересным и любимым предметом. Все это положительно скажется на успеваемости в школе, ведь, когда учеба дается легко, заниматься намного веселее.

Все это делает обучение ментальной арифметике самым продуктивным способом освоения быстрого устного счета.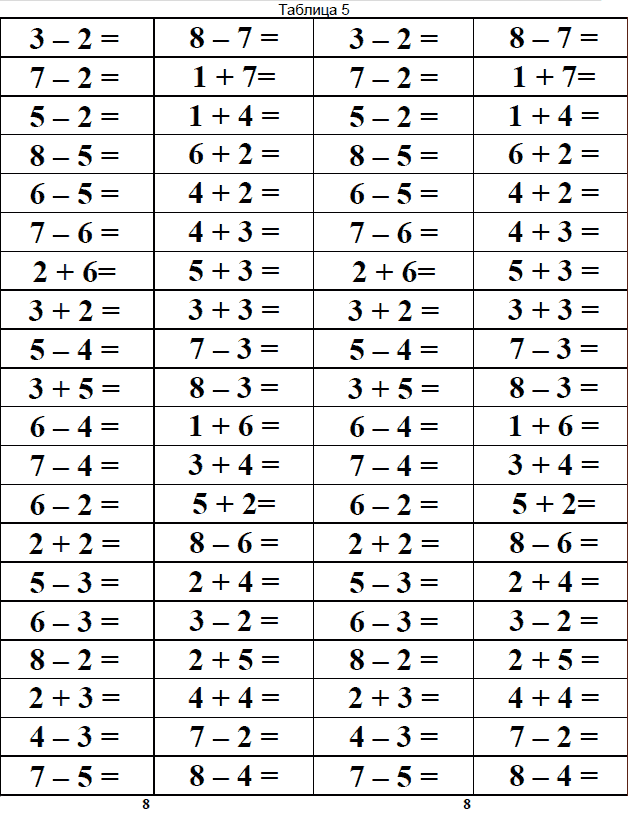 Ребенку больше не придется прибегать к различным математическим хитростям, чтобы легко справляться с задачами и примерами. Ученик приобретает навыки, которые сохраняются на всю жизнь, а значит они пригодятся ему не только в учебе, но и в карьерной деятельности. Все это делает обучение данной технике отличным вкладом в будущее своего ребенка.

Счет в уме – тренировка умственных способностей

В современном мире огромное значение придается саморазвитию. Так в сферу интересов многих людей попадает умение быстро считать в уме. Существует целый ряд методик, позволяющих устно выполнять операции даже с большими числами. Рассмотрим самые популярные из них и определим, как они справляются со своей задачей.

Польза навыков устного счета

Числа – это то, что окружает современного человека повсюду. Мы знакомимся с ними в детстве на уроках математики или еще до школы. Именно в это время прививаются первичные навыки счета, позволяющие производить более сложные вычисления в дальнейшем. В начальной школе большое значение уделяется устному счету. Учителя проверяют то, насколько хорошо ребенок умеет складывать, вычитать, умножать и делить небольшие числа в уме. Но чем старше становится ученик, тем реже он считает устно, предпочитая производить вычисления на бумаге или с помощью калькулятора.

Во взрослой жизни тенденция отказа от устного счета сохраняется. Совершая покупки или выполняя отчет по работе, гораздо проще воспользоваться умными помощниками, чем тратить время и силы на попытки подсчитать все в уме. Но в нужный момент гаджетов или листа бумаги может не оказаться под рукой. В таких ситуациях человек невольно задумывается о том, насколько полезным может быть навык быстрого устного счета, ведь вычисления в уме позволяют сделать любую работу, связанную с цифрами, более продуктивной. Но как этого можно добиться?

Первым способом является знание хитростей математики. Существует целый ряд приемов, позволяющих не только складывать и вычитать, но умножать и делить двузначные и трехзначные числа. Но у данного подхода есть свои минусы, главным из которых является невозможность применять один и тот же прием для разных чисел. К тому же, многие способы включают в себя сразу несколько действий. Учитывая то, что вычисления ведутся устно, бывает сложно сохранять концентрацию и не сбиваться.

Более продуктивной альтернативой математическим хитростям является такая методика счета в уме, как ментальная арифметика. Она позволяет научиться производить операции даже с многозначными числами за считанные секунды. К ее плюсам можно отнести уже то, что ей может обучиться как маленький ребенок, так и взрослый. В чем же секрет этой техники?

Как научиться считать ментально

Ментальная арифметика – это методика, позволяющая научиться считать в уме без использования подручных средств. В ее основе лежит умение производить вычисления на абакусе – специальных счетах, известных еще с древних времен. Обучение этой технике проходит поэтапно. Сначала ученику предстоит освоить принципы работы абакуса, научиться использовать его для простейших операций с небольшими числами. Требуется хорошо закрепить эти навыки, довести их до автоматизма. Только тогда, когда удастся производить вычисления не задумываясь, можно будет перейти к следующему этапу тренировок.

Теперь у ученика появляется другая задача – научиться представлять абакус в своем воображении и считать уже на нем. Сначала изучается сложение и вычитание небольших чисел, затем осваивается умножение и деление. Постепенно уровень сложности растет, и ученик переходит к операциям с многозначными числами. Этому этапу тренировок счета в уме уделяется особенно много времени и внимания, но результат будет стоить потраченных усилий. Так удастся производить вычисления даже быстрее, чем при использовании калькулятора, но и это не является главным плюсом данной методики.

Помимо быстрого устного счета, ментальная арифметика развивает множество других функций человеческого интеллекта. Обычно при подсчетах используется только левое полушарие мозга, которое отвечает за логическое мышление и аналитические способности, а правое, отвечающее за креативное мышление и фантазию, не задействуется. Но ментальный счет имеет совершенно другой подход, ведь в его основе лежат вычисления на воображаемых счетах, а значит правое полушарие также будет использоваться. Рассмотрим то, как это отражается на умственных способностях человека.

Тренировка интеллектуальных способностей

Человеческий мозг нуждается в тренировке. Только получая нагрузку на различные области интеллекта, удается совершенствовать свои способности. Ментальная арифметика отлично справляется с этой задачей, так как задействует оба полушария мозга одновременно. Благодаря этому удается:

улучшить память. Обучение включает в себя упражнения, в которых нужно производить операции с целыми рядами чисел подряд. Из-за этого приходится одновременно держать в уме итог промежуточных вычислений и новые части задания. Такая разносторонняя нагрузка способствует развитию памяти.
повысить концентрацию. Работа с большим объемом чисел требует высокой сосредоточенности. Обучаясь ментальной арифметике, человек также учится сохранять внимание на процессе вычислений. Концентрация, которая развивается в процессе занятий, будет очень полезна и в других сферах деятельности.
укрепить межполушарные связи. Те или иные задачи нагружают в большей степени или левое, или правое полушарие мозга. Ментальная арифметика позволяет укрепить связь между ними, благодаря чему удается добиться более продуктивной работы как в творческих, так и в аналитических областях.
развить творческие способности и фантазию. Креативное мышление важно в самых разных сферах деятельности. Ментальная арифметика хоть и подразумевает работу с числами, но также способствует повышению и творческих способностей человека.
улучшить логические способности. Выполнение большого количества операций с числами развивает левое полушарие мозга, что положительно сказывается на логических и аналитических функциях интеллекта.
увеличить количество процессов, которые можно выполнять одновременно. Освоение ментальной арифметики формирует многозадачность, благодаря которой можно научиться считать большое количество чисел в уме и параллельно выполнять другие действия – рассказывать стихотворение или петь песню. Умение выполнять несколько дел одновременно очень полезно в повседневной жизни.

Помимо перечисленных плюсов, ментальная арифметика несет в себе различные преимущества для каждой возрастной группы. Для детей такие занятия – это способ полюбить математику, улучшить успеваемость в школе и повысить мотивацию к учебе. Для взрослых эта техника является отличным инструментом саморазвития, ведь она позволяет приобрести навыки, которые пригодятся и в работе, и в быту. Все это делает данную методику отличным вариантом для тех, кто хочет улучшить свои способности. Осталось определиться с тем, как лучше организовать сам процесс обучения.

Ментальная арифметика – методика обучения быстрому счету в уме

Как и многие другие программы, данную методику можно освоить самостоятельно. Но поиск нужного материала, отсутствие помощи педагога и необходимость соблюдать регулярность тренировок могут стать серьезной преградой для обучения. Именно поэтому большинство людей отдает предпочтение очным курсам, а не самостоятельным тренировкам. Но и у такого подхода есть свои минусы:

приходится тратить время на дорогу. Из-за современного ритма жизни, потеря пусть даже и одного часа на дорогу очень ощутима. Далеко не у каждого взрослого или ребенка есть на это время.
нельзя регулировать график и время занятий. Сменный график работы у взрослых или наличие секций у детей может препятствовать посещению курсов ментальной арифметики. Из-за этого такие занятия являются не тем вариантом, который удобен для всех.
нет возможности индивидуально подобрать нагрузку. У каждого человека свое количество свободного времени, которое он может посвятить саморазвитию. Групповые тренировки подразумевают постоянное посещение. Тренер не сможет ждать тех, кто не справляется с нагрузкой из-за пропуска занятий.

Все это приводит к востребованности онлайн-обучения, в том числе, и ментальной арифметике. Теперь изучать быстрый счет в уме можно прямо из дома и тогда, когда это удобно. Так как для занятий достаточно компьютера и выхода в интернет, можно беспрепятственно путешествовать, не пропуская онлайн-уроки. А возможность индивидуально подобрать нагрузку и график тренировок позволяет самосовершенствоваться даже самым занятым маленьким и взрослым ученикам.

Быстрый устный счет упражнения. Как освоить устный счёт школьникам и взрослым

Гаусс и устный счет

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10 . В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10 ». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10 , а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6 . Чтобы из 8 получить 10 , не хватает 2 . Затем к 10 останется прибавить 4=6-2 . В итоге получаем: 8+6=(8+2)+4=10+4=14

Пусть нам нужно сложить два числа: 356 и 728 . Число 356 можно представить как 300+50+6 . Аналогично, 728 будет иметь вид 700+20+8 . Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Например, сколько будет 528-321 ? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1 .

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4 , это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения . Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6 . Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32 . Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57 . Это значит, что на нужно взять число «79 » 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50 , а потом – 79 на 7 .

79*50=(70+9)*50=3500+450=3950
79*7=(70+9)*7=490+63=553
3950+553=4503

Умножение на 11

Чтобы умножить двузначное число на 11 , две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11 .

Проверим и умножим 54 на 11 .

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n , то следующей за ней по иерархии цифрой будет n+1 . Результат заканчивается на квадрат последней цифры, то есть квадрат 5 .

Проверим! Возведем в квадрат число 75 .

Деление чисел в уме

Деление на однозначное число

Например, есть число 6144 , которое нужно разделить на 8 . Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600 . Представим пример в виде:

6144:8=(5600+544):8=700+544:8

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656 . По правилу, последняя цифра в получившемся числе будет 0 , так как 5*6=30 . Действительно, 1325*656=869200 .

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56 ?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424 . Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70 . Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4 . Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79 , второй вариант обязательно оказался бы верным.

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

Не забывайте тренироваться каждый день;
не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Тренажер устного счета — легко и существенно повышает интеллектуальный потенциал человека.

Результатом приобретения навыков и здачи нормативной квалификации будет присвоение спортивного разряда (I разряд, II разряд, III разряд, кандидат в мастера спорта, мастер спорта и гроссмейстер).

Людей из группы выделяют как по умению красиво и правильно говорить, так и по умению быстро считать в уме, и относят их, как правило, к категории умных. Школьнику умение быстро считать в уме позволяет более успешно учиться, а инженеру и ученому сократить время получения результата их деятельности.
УС нужен не только школьникам, но и инженерам, учителям, медицинским работникам, ученым и руководителям разного уровня. Кто быстро считает, тому легче учиться и работать. УС – это не игрушка, хотя и развлекает. Он позволяет вернуться ученику на те “рельсы”, с которых он упал когда-то; повышает скорость и качество восприятия информации; дисциплинирует и производит точность во всем; приучает замечать детали и мелочи; приучает к экономии; создает образы предметов и явлений; позволяет предвидеть будущее и развивает интеллект человека.
«Евроремонт» в голове нужно начинать с простых арифметических действий, которые позволяют структурировать мозг.
Умение быстро считать в уме дает ученику уверенность в себе. Как правило, быстрее всех считают в уме те, кто хорошо учится в школе или в ВУЗе. Если отстающего ученика научить быстро считать в уме, то это обязательно благотворно повлияет на его успеваемость, и не только в естественных, но и во всех других предметах. Это доказано практикой.
Произвольное внимание и интерес во время устного счета меняет блуждающий взгляд отстающего ученика на фиксированный, а концентрация внимания достигает нескольких этажей глубины предмета или процесса, который изучается.
“Изучение математики дисциплинирует мышление, приучает к правильному словесному выражению мыслей, к точности, сжатости и ясности речи, воспитывает настойчивость, умение достигать намеченной цели, развивает работоспособность, способствует правильной самооценке владения предметом, который изучается”. (Кудрявцев Л.Д. – член-кор. РАН. 2006.).
Ученик, который научился быстро считать в уме, как правило, начинает и быстрее мыслить.
Тот, кто по своей природе хорошо считает, естественно обнаружит ум и в любой другой науке, а тот, кто считает медленно, учась этому искусству и овладевая им, сможет улучшить свой ум, сделать его острее (Платон).
Приобретенных навыков устного счета одним хватит на 5 — 10 лет, а другим на всю жизнь.
Нашим потомкам будет легче учиться и получать знания. Однако, культура устного счета всегда будет являться неотъемлемой частью общечеловеческой культуры.
Кто быстро считает в уме, тот, как правило, ясно мыслит, быстро воспринимает и глубже видит.
Освоение УС развивает образное, диаграммное и системное мышление, расширяет оперативную память, диапазон восприятия, приучает к мышлению на несколько ходов вперед, повышает качество мышления, оперируя количественными характеристиками объектов.
УС повышает ясность мышления, уверенность в себе, а также волевые качества (терпение, усидчивость, выносливость, трудолюбие). Приучает к глубокой и устойчивой концентрации внимания, домысливанию и договариванию начатых фраз (особенно у дошкольников и учеников начальных классов).

Умение считать в уме – полезный навык не только в стенах школы, но и в обычной жизни. С его помощью можно почти моментально и безошибочно производить любые действия с числами без помощи калькулятора или бумаги. Сегодня будем говорить о развитии навыков устного счета, рассмотрим полезные упражнения и дадим советы.

Плюсы устного счета

Счетным навыкам нас обучают с детства. Это элементарные операции сложения, вычитания, умножения и деления. В случае небольших чисел с ними легко справляются даже младшие школьники, но задача существенно усложняется, когда нужно произвести действие с двузначным или трехзначным числом. Однако с помощью тренировки, несложных упражнений и маленьких хитростей вполне можно подчинить данные операции быстрой умственной обработке.

Возможно, вы спросите, зачем это нужно, ведь существует такая удобная вещь, как калькулятор, а на крайний случай под рукой всегда есть бумага для осуществления вычислений. Быстрый счет в уме дает массу преимуществ:

Экономия времени. Рассчитать стоимость покупок в магазине или кафе и проверить правильность сдачи, опередить одноклассников в решении примера или написании теста — все это возможно, если вы хорошо считаете в уме.
Возможность обратиться к другим аспектам задачи. Зачастую задачи содержат в себе, как минимум, две стороны: чисто арифметическую (действия с числами) и интеллектуально-творческую (выбор подходящего решения для конкретной задачи, нестандартный подход для более быстрого решения и др.). Если школьник недостаточно хорошо и быстро справляется с первой стороной, то от этого страдает вторая: концентрируясь на выполнении арифметической составляющей, ребенок не задумывается над смыслом задачи, может не увидеть подвоха или более простого решения. Если же счетные операции доведены до автоматизма или просто не требуют большого количества времени, то «включается» детальное рассмотрение смысла задачи, появляется возможность применения творческого подхода к ней.
Тренировка интеллекта. Счет в уме позволяет держать интеллект в тонусе, постоянно задействовать мыслительные процессы. Особенно это характерно для действий с большими числами, когда мы подбираем способ для максимального упрощения операции.

Упражнения с таблицами

Упражнения рассчитаны на детей любого возраста, испытывающих затруднения при выполнении операций с простыми числами (одно- и двузначными). Позволяет натренировать навыки устного счета, довести до автоматизма несложные арифметические операции.

Необходимые материалы: для выполнения упражнений понадобится сетка одно- и двузначных чисел. Пример:

В первом столбце располагаются числа, с которыми нужно выполнять действия. Во втором – ответы на эти действия. С помощью специально вырезанной закладки можно проверить правильность вычисления. Например:

Картинка из книги: Посталовский И.З. «Тренировочные таблицы для автоматизации устного счета»

Варианты упражнений:

Последовательно сложи в уме пары чисел в сетке. Назови ответ вслух и проверь себя с помощью второго столбца и закладки. Задание может выполняться в свободном темпе или на время.
Последовательно выполни вычитание в уме чисел из сетки.
Последовательно сложи в уме пары чисел в сетке. Прибавь к каждой сумме цифру 5 и назови ответ вслух.
Последовательно сложи в уме тройки чисел в сетке.
Последовательно со всеми числами в сетке выполни следующие действия: прибавь нижнее число, из полученной суммы вычти следующую в столбце цифру.

На основе подобных таблиц можно формировать любые задания. Сетки составляются в зависимости от модификации упражнения.

ВАЖНО! Чтобы упражнение дало результат, оно должно выполняться регулярно, до полного усвоения навыка.

Осваиваем умножение

Упражнение предназначено для детей, освоивших таблицу умножения от 1 до 10. Тренирует навык перемножения двузначного числа на однозначное.

Составляется столбик из произвольных двузначных чисел. Задание для ребенка: последовательно умножить эти числа сначала на 1, потом на 2, на 3 и т.д. Ответ произносится вслух. Выполняется до тех пор, пока ответы не запомнятся и не будет выдаваться автоматически.

Главное – внимание

Так что, говорите, надо решить?

Задание: сложи последовательно числа: 3000 + 2000+ 30 + 2000 + 10 + 20 + 1000 + 10 + 1000 + 30 =

Назови ответ. Проверь себя с помощью калькулятора.

Если ответ получился верным, необходимо закрепить успех и прорешать еще несколько подобных примеров (могут составляться произвольно). Если в ответе была ошибка, нужно вернуться к последовательности чисел и исправить ее.

В чем идея: В результате сложения чисел получается сумма 9100. Но если делать это невнимательно, будет автоматически напрашиваться ответ 10000 (мозг стремится округлить сумму, сделать ответ более красивым). Поэтому очень важно сохранять контроль за своими действиями при производстве арифметических задач в несколько действий.

Возможные примеры:

3000 – 700 — 60 – 500 — 40 – 300 -20 – 100 =

100:2:2*3*2 + 50 – 100 + 200 – 30 =

Если большинство примеров решается с ошибками (НО! не связанными с умением считать в принципе), то есть смысл повысить концентрацию внимания. Для этого можно:

Минимизировать внешние раздражители. Например, по возможности выйти в другую комнату, выключить музыку, закрыть окно и т.д. Если необходима концентрация на примере во время урока, когда нет возможности выйти и добиться полной тишины, нужно закрыть глаза и представить цифры, с которыми осуществляются действия.
Добавить элемент состязательности. Зная, что верное и быстрое решение принесет победу над противником и/или какое-то поощрение, ученик более охотно сосредоточится на цифрах и предпримет максимум усилий в процессе вычисления.
Устанавливать личные рекорды. Можно визуализировать все ошибки, совершенные школьником в процессе вычисления. Например, нарисовать цветок с крупными лепестками (количество лепестков = количеству решаемых примеров). Черным будет закрашено столько лепестков, сколько примеров было решено с ошибками.2=2500-4=2496

P.S. Данные правила могут существенно упростить устный счет, однако необходимы регулярные тренировки, чтобы в нужный момент можно было правильно воспользоваться правилом. Поэтому рекомендуется прорешать такое количество примеров на каждое из них, которое позволит автоматизировать навык. Для начала можно записывать расчеты на бумаге, постепенно сокращая количество написанного и переводя операции в мыслительный план. В первое время также рекомендуется проверять свои ответы при помощи калькулятора или стандартных вычислений в столбик.

Гаусс и устный счет

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10 . В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10 ». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10 , а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Пусть нам нужно сложить два числа: 356 и 728 . Число 356 можно представить как 300+50+6 . Аналогично, 728 будет иметь вид 700+20+8 . Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Например, сколько будет 528-321 ? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1 .

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4 , это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения . Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

Умножение многозначных чисел на однозначные

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32 . Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57 . Это значит, что на нужно взять число «79 » 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50 , а потом – 79 на 7 .

79*50=(70+9)*50=3500+450=3950
79*7=(70+9)*7=490+63=553
3950+553=4503

Умножение на 11

Чтобы умножить двузначное число на 11 , две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11 .

Проверим и умножим 54 на 11 .

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n , то следующей за ней по иерархии цифрой будет n+1 . Результат заканчивается на квадрат последней цифры, то есть квадрат 5 .

Проверим! Возведем в квадрат число 75 .

Деление чисел в уме

Деление на однозначное число

6144:8=(5600+544):8=700+544:8

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656 . По правилу, последняя цифра в получившемся числе будет 0 , так как 5*6=30 . Действительно, 1325*656=869200 .

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56 ?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424 . Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70 . Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4 . Согласно таблице умножения, нам подходят результаты 4 и 9 . Логично предположить, что результатом деления может быть либо число 74 , либо 79 . Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79 , второй вариант обязательно оказался бы верным.

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

Не забывайте тренироваться каждый день;
не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

В устном счете, как и везде, есть свои хитрости, и чтобы научиться быстрее считать нужно, знать эти хитрости и уметь применять на практике.

Сегодня мы этим и займемся!

1. Как быстро складывать и вычитать числа

Рассмотрим три случайных примера:

25 – 7 =
34 – 8 =
77 – 9 =

Типа 25 – 7 = (20 + 5) – (5- 2) = 20 – 2 = (10 + 10) – 2 = 10 + 8 = 18

Согласитесь, что такие операции сложно проворачивать в голове.

Но есть более простой способ:

25 – 7 = 25 – 10 + 3, так как -7 = -10 + 3

Намного проще вычесть из числа 10 и прибавить 3, чем городить сложные вычисления.

Вернемся к нашим примерам:

25 – 7 =
34 – 8 =
77 – 9 =

Оптимизируем вычитаемые числа:

Вычесть 7 = вычесть 10 прибавить 3
Вычесть 8 = вычесть 10 прибавить 2
Вычесть 9 = вычесть 10 прибавить 1

Итого получим:

25 – 10 + 3 =
34 – 10 + 2 =
77 – 10 + 1 =

Вот теперь намного интересней и проще!

Посчитайте сейчас представленные ниже примеры этим способом:

91 – 7 =
23 – 6 =
24 – 5 =
46 – 8 =
13 – 7 =
64 – 6 =
72 – 19 =
83 – 56 =
47 – 29 =

2. Как быстро умножать на 4, 8 и 16

В случае умножения мы тоже разбиваем числа на более простые, например:

Если помните таблицу умножения, то все просто. А если нет?

Тогда нужно упростить операцию:

Наибольшее число ставим первым, а второе раскладываем на более простые:

8 * 4 = 8 * 2 * 2 = ?

Удваивать числа гораздо легче, нежели чем учетверять или увосьмирять их.

Получаем:

8 * 4 = 8 * 2 * 2 = 16 * 2 = 32

Примеры раскладывания чисел на более простые:

4 = 2*2
8 = 2*2 *2
16 = 22 * 2 2

Отработайте этот способ на следующих примерах:

3 * 8 =
6 * 4 =
5 * 16 =
7 * 8 =
9 * 4 =
8 * 16 =

3. Деление числа на 5

Возьмем следующие примеры:

780 / 5 = ?
565 / 5 = ?
235 / 5 = ?

Деление и умножение с числом 5 всегда очень простые и приятные, ведь пять это половина от десяти.

И как их быстро решить?

780 / 10 * 2 = 78 * 2 = 156
565 /10 * 2 = 56,5 * 2 = 113
235 / 10 * 2 = 23,5 *2 = 47

Для того чтобы проработать этот способ решите следующие примеры:

300 / 5 =
120 / 5 =
495 / 5 =
145 / 5 =
990 / 5 =
555 / 5 =
350 / 5 =
760 / 5 =
865 / 5 =
1270 / 5 =
2425 / 5 =
9425 / 5 =

4. Умножение на однозначные числа

С умножением немного сложнее, но не сильно, как бы Вы решили следующие примеры?

56 * 3 = ?
122 * 7 = ?
523 * 6 = ?

Без специальных фишек решать их не очень приятно, но благодаря методу «Разделяй и властвуй» мы можем сосчитать их гораздо быстрее:

56 * 3 = (50 + 6)3 = 50 3 + 6*3 = ?
122 * 7 = (100 + 20 + 2)7 = 100 7 + 207 + 2 7 = ?
523 * 6 = (500 + 20 + 3)6 = 500 6 + 206 + 3 6 =?

Нам остается только перемножить однозначные числа, некоторые из которых с нулями и сложить полученные результаты.

Для проработки этой техники решите следующие примеры:

123 * 4 =
236 * 3 =
154 * 4 =
490 * 2 =
145 * 5 =
990 * 3 =
555 * 5 =
433 * 7 =
132 * 9 =
766 * 2 =
865 * 5 =
1270 * 4 =
2425 * 3 =

Делимость числа на 2, 3, 4, 5, 6 и 9

Проверьте числа: 523, 221, 232

Число делится на 3, если сумма его цифр делится на 3.

Например, возьмем число 732, представим его как 7 + 3 + 2 = 12. 12 делится на 3, а значит, число 372 делится на 3.

Проверьте, какие из следующих чисел делятся на 3:

12, 24, 71, 63, 234, 124, 123, 444, 2422, 4243, 53253, 4234, 657, 9754

Число делится на 4, если число, состоящее из последних двух его цифр, делится на 4.

Например, 1729. Последние две цифры образуют 20, которое делится на 4.

Проверьте, какие из следующих чисел делятся на 4:

20, 24, 16, 34, 54, 45, 64, 124, 2024, 3056, 5432, 6872, 9865, 1242, 2354

Число делится на 5, если его последняя цифра 0 или 5.

Проверьте, какие из следующих чисел делятся на 5 (самое легкое упражнение):

3, 5, 10, 15, 21, 23, 56, 25, 40, 655, 720, 4032, 14340, 42343, 2340, 243240

Число делится на 6, если оно делится и на 2 и на 3.

Проверьте, какие из следующих чисел делятся на 6:

22, 36, 72, 12, 34, 24, 16, 26, 122, 76, 86, 56, 46, 126, 124

Число делится на 9, если сумма его цифр, делится на 9.

Например, возьмем число 6732, представим его как 6 + 7 + 3 + 2 = 18. 18 делится на 9, а значит, число 6732 делится на 9.

Проверьте, какие из следующих чисел делятся на 9:

9, 16, 18, 21, 26, 29, 81, 63, 45, 27, 127, 99, 399, 699, 299, 49

Игра «Быстрое сложение»

Ускоряет устный счет
Тренирует внимание
Развивает творческое мышление

Отличный тренажер для развития быстрого счета. На экране дана таблица 4х4, а над ней показаны числа. Самое большое число нужно собрать в таблице. Для этого нажмите мышкой на два числа, сумма которых равна этому числу. Например, 15+10 = 25.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Задание на сегодня

Решить все примеры и тренироваться минимум 10 минут в игре Быстрое сложение.

Очень важно отработать все задания этого урока. Чем лучше Вы будете выполнять задания, тем больше будет пользы. Если Вы чувствуете, что Вам мало заданий — можете сами составлять себе примеры и решать их и тренироваться в математические развивающие игры.

Урок взят из курса «Устный счет за 30 дней»

Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. Научу использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Другие развивающие курсы

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.

После прохождения курса ребенок сможет:

В 2-5 раз лучше запоминать тексты, лица, цифры, слова
Научится запоминать на более длительный срок
Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Как научить ребенка устному счету: 9 важных советов

Ранее мы писали о том, как правильно давать ребенку карманные деньги, научить его определять время по часам и рассказать, откуда берутся дети. Сегодня поговорим о том, как научить его считать в уме. Сделать это не так просто, но вполне реально, если следовать советам, описанынм нами ниже.

Обратите внимание на возраст

Специалисты считают, что лучше всего начинать обучение ребенка в возрасте трех-четырех лет. Однако сначала нужно давать небольшие нагрузки, ведь дети быстро устают. 10-15 минут обучения — уже неплохой результат.

Необходимо заинтересовать

Как уже говорилось выше, дети в раннем возрасте хорошо запоминают только то, что им интересно. Поэтому нужно заинтересовать ребенка, когда речь заходит об устном счете.

В этом деле необходимо проявить чуткость и смекалку. Следует знать, чем ребенок интересуется, что ему нравится, чтобы найти способы обыграть это.

В обучении помогут специальные мультики, коих на просторах интернета очень много, притом как старых, так и современных. Можно использовать другие инструменты, такие как, например, игровые кубики и иные игрушки, а также придумывать различные игры, связанные со счетом.

Просите ребенка применять знания

Когда ребенок получит знания, нужно закреплять их. Лучше всего это делать, применяя знания на практике. Можно, например, просить ребенка считать шаги, свои игрушки. Можно давать ему простые импровизированные задачки для наглядности: например, поставить перед ним некоторое количество машинок/солдатиков/кукол попросить их сосчитать, а затем убрать несколько единиц и попросить сосчитать еще раз.

Не следует зацикливаться на «единичном» счете

Для начала научиться считать по единицам — это очень полезно. Однако надолго зацикливаться на этом нельзя, следует переходить к группам чисел, математическим действиям с числами в пределах двух десятков. Эксперты считают, что счет на пальцах или палочках не способен включить долговременную память, что оказывает негативное влияние на дальнейшее развитие способностей к счету.

Отучать от счетного материала нужно после достижения пятилетнего возраста, советуют специалисты.

Соблюдайте очередность

Информация должна поступать и запоминаться структурированно и поочередно. Начинать нужно с простого, а затем повышать сложность.

Кроме того, нужно помнить, что процесс запоминания информации ребенком состоит из трех этапов: привыкания к ней, ее осознания понимания, а затем собственно запоминания. Этот порядок нарушать нельзя ни в коем случае.

Сначала научите ребенка «единичному» счету, например, на пальцах, до пяти, а затем до десяти. Параллельно с этим уже следует просить ребенка решать математические задачи — прибавлять и складывать, загибая или добавляя пальцы, считать получившееся их количество. Затем, когда вы удостоверитесь, что ребенок хорошо все усвоил, можно двигаться дальше, к счету до 20 и более сложным задачкам.

К пяти годам ребенок должен научиться складывать и вычитать в уме числа в пределах десяти «на автомате».

Не занимайтесь чересчур много

Важно не перегружать ребенка, особенно, если он еще совсем мал. Будет достаточно 10-15 минутных занятий. В противном случае чадо будет уставать, а такая учеба, конечно же, не даст никакого результата. Однако заниматься по 10-15 минут можно несколько раз в день.

Не нужно повторять каждый день

Пройденный и усвоенный ребенком материал не обязательно повторять каждый день. Гораздо эффективнее будет применять его при необходимости, например для решения более сложных задач. Так материал запомнится еще лучше.

Не ругайте

Важно! Если что-то не получается, или получается не так быстро, как вы себе это представляли, не стоит ругать ребенка. Имейте терпение и всячески помогайте малышу, тогда вскоре у него все получится.

Пользуйтесь специальными средствами и литературой

Глупо будет не воспользоваться многолетним опытом поколений, изложенным в специальной литературе. Есть достаточно много различных книг с разными методиками, которые помогут научить ребенка считать в уме. Какие-то из них могут оказаться более эффективными, какие-то — менее. Все зависит от конкретного случая.

Также можно купить специализированные наборы для счета, которые разработаны для того, чтобы ребенок быстро и весело научился считать, и ему при этом было интересно.

Фото: из открытых источников

способов научить счет — PreKinders

Facebook
Твиттер
Pinterest

Вот 15 способов научить навыкам счета в Pre-K.

Наборы для изготовления

Используйте учетные карточки для небольших счетных циновок. Дети отсчитывают наборы на каждой карточке. (На этом фото дети считали наборы по 2 штуки.)

Подсчет ящиков для мусора

Я использовал доски для сухого стирания в качестве счетного «коврика», на котором дети могли ставить свои счетчики. Я написал цифру на доске для сухого стирания каждого ребенка, затем попросил их определить цифру и отсчитать это количество счетчиков на своей доске. После того, как я проверил их работу, они могли стереть номер, а я написал новый номер на их доске. Каждый ребенок мог работать в своем собственном темпе и на своем уровне способностей. Некоторые дети работали над числами от 1 до 5, а другие считали больше 10.

Для математических счетчиков можно собрать множество интересных материалов. Некоторые идеи — пластиковые ящерицы или жуки из долларового магазина, пластмассовые драгоценности, маленькие пенистые фигурки, ключи, ракушки.

Карты с точками

Карточки с точками изготавливаются из учетных карточек и наклеек с цветными точками. Я сделал карточку для каждого числа 1-10, с цифрой, написанной рядом с точками. Дети считают вслух вслух, ставя каждый математический счетчик на каждую точку. Они используют их, когда начинают учиться счету, чтобы помочь им разместить правильное количество математических фишек на карточке.Загрузите точечные карточки для печати.

Подсчет фруктов

Я нанес точки наклеек на одноразовые пластиковые тарелки и покрыл середину прозрачной контактной бумагой. На каждой пластине разное количество точек. Дети считают точки на тарелке, произносят число, затем считают количество фруктов и кладут на тарелку. Если счетчики фруктов недоступны, можно использовать любой тип счетчика. Они похожи на карты с точками выше, за исключением того, что я не писал цифры рядом с точками, потому что в этой игре целью был подсчет и только однозначное соответствие, а не определение числа.

Путь Игры

Дети бросают игровой кубик и подсчитывают количество мест, на которые можно переместить свою игровую фишку. Игры с путями могут быть разработаны так, чтобы соответствовать различным уровням навыков, так же, как и игры с сеткой.

Игры на счет и совпадение

Я сделал этот набор из плаката, наклеек на машину и прозрачной контактной бумаги. Каждое число представляет собой две карточки. Дети считают машины на каждой карточке и сравнивают карточки с одинаковым количеством машин.Я позаботился о том, чтобы наклейки располагались по-разному, чтобы они не казались одинаковыми на первый взгляд (их действительно нужно пересчитывать).

Домино

Дети считают и сравнивают количество точек на домино.

Марки для лепки

Дети нажимают числовой штамп в пластилине и отсчитывают количество шариков, которое нужно вдавить в пластилин. (Эти марки для пластилина были доставлены из Лейкшора.)

Наборы нумерованных чертежей

Дети рисуют простые картинки (радуги, цветы, солнышки, воздушные шары, человечки и т. Д.)) для обозначения числа. Например, для числа 3 они могут нарисовать 3 солнца.

Рыбная ловля

Дети используют навыки числовой идентификации и счета, чтобы расположить числовую рыбку по порядку на синем фетре (пруд). Я сделал их, написав цифры на поролоновой рыбе из магазина для рукоделия (вы можете использовать любую форму поролона).

Игра божья коровка

В этой игре 2 уровня. На одной стороне палочек написано число, на котором выбито количество божьих коровок.Дети идентифицируют число, затем кладут каждый жетон божьей коровки на божью коровку на палке, считая вслух. На оборотной стороне ручки есть цифра, написанная на ней, но не проштампованная. Более продвинутые дети могут использовать немаркированную сторону, а затем самостоятельно проверить свой ответ, проверив обратную сторону.

Счетные самолеты

Каждый месяц мы отслеживали, сколько самолетов пролетело над нашей игровой площадкой, пока мы были на улице. Когда дети видели на улице самолеты, мы в голове вели счет (обычно пролетало не более трех).Затем, когда мы заходили внутрь, мы добавляли столько самолетов к нашей карте. Детей часто видели на карте, считая, сколько мы уже видели.

Номерная книга

На фото изображена сделанная нами книга для подсчета пауков. Дети определили число, затем отметили это количество кругов на странице маркером бинго. Карандашом нарисовали ноги и глазки. Я всегда убеждаюсь, что детям комфортно считать с помощью манипуляторов, прежде чем делать книгу с числами, чтобы они не разочаровались, пытаясь сделать книгу без ошибок.

Носки Mystery

Дети работают с партнером, чтобы играть в эту игру. Им понадобится один носок и 5 плоских цветочных шариков (плоские шарики отлично подходят для математических манипуляций, потому что они не скатываются). Один ребенок кладет в носок несколько шариков. Другой ребенок, не выглядывая, тянется к носку, считает шарики на ощупь и называет число. Затем дети могут вынуть шарики из носка, чтобы проверить правильность ответа.

Ювелирные изделия

Струны для драгоценных камней — это струны из цветных пластиковых драгоценных камней, которые разрезаются на сегменты по 1 драгоценному камню на струну, 2 камня на струну, 3 камня на струну и так далее (до 10).Каждому ребенку нужен один набор цепочек с драгоценными камнями 1–10 и набор карточек с цифрами 1–10. Дети берут из контейнера по одной нитке драгоценных камней, подсчитывают количество драгоценных камней на веревке и сопоставляют ее с правильной цифровой карточкой.

Узнайте больше о способах обучения счету здесь.

Добро пожаловать!

Хотите подписаться на мою БЕСПЛАТНУЮ еженедельную рассылку обновлений? Присоединяйтесь к более чем 85 000 подписчиков!

17 фантастических идей для обучения механическому счету — раннее обучение

Один из основных навыков, составляющих основу раннего математика, это умение механически считать. Механический подсчет — это просто произнесение чисел по порядку, обычно начиная с единицы, например 1,2,3,4,5 и т. Д. Это не значит подсчет предметов или подсчет действий, хотя это связано с этими навыки. Это просто означает произнесение чисел по порядку, ни с чем не связанное.

Как научить механическому счету? Обучайте механическому счету с помощью простых песен, которые ведут счет вверх. Подсчет простые действия и предметы, которые появляются в повседневной жизни, также рекомендуется, например, для подсчета лестниц. Позже такие игры, как счет во время хлопки в ладоши или марш помогают процессу.

Механический подсчет может быть забавным! Это просто и обычно требует очень мало подготовки или ресурсов для воплощения в жизнь.

Узнайте 16 лучших способов научить детей механическому счету и попробуйте сами сегодня! Если вы хотите узнать больше о том, что такое механический подсчет, ознакомьтесь с этим подробным руководством.

1. Счет, используя разные голоса!

Дети любят брать на себя роли и смешные голоса персонажей. Это занятие подкрепляет этот энтузиазм и использует его для механического подсчета жизнь!

Когда я занимаюсь этим, я всегда использую кости, которые у меня есть. сделано, на котором изображены разные персонажи. Эти кости начали свою жизнь как часть столба забора, и я просто распилил его на куб и нарисовал символы на нем с помощью перманентного маркера.

Нарисуйте на кубиках персонажей со смешными или отчетливыми голосами.На игральных костях я нарисовал принцессу, мышь, робота, инопланетянина, тигра и призрака. Призрак — мой особый фаворит! Игральные кости «Голос персонажа» — неизменный фаворит для игр со счетом.

Идея состоит в том, что вы бросаете кости и смотрите, что у вас получится. пример робота. Затем вы просто считаете, используя голос робота — 1, 2, 3… Попробуйте и используйте роботизированное оружие и действительно воплотите его в жизнь. Считайте до тех пор, пока ребенок может управляйте и определенно переходите только после десяти, если можете.

Затем бросьте кости и попробуйте другой голос.

Если вам не нравится DIY, вы можете сделать простые игральные кости другим способом или просто попросите детей выбрать, какой голос они могут использовать. Это прекрасно работает, и механический подсчет определенно не то, для чего вам нужно много ресурсов.

Эта игра — одна из моих любимых игр из 21 дошкольного кружка, на которую вы можете взглянуть здесь.

2. Счет с марионеткой

Дети очень любят кукол, и по какой-то странной причине часто слушают марионеток лучше, чем настоящих взрослых людей.

Окунитесь в эту странную магию, используя марионеток для механики подсчет!

Если вы родитель, марионетка — отличная вещь, которую можно использовать с вашим ребенком, чтобы привлечь его внимание, и то же самое верно, если вы педагог.

Это можно сделать несколькими способами. Самый простой — получить марионетка считать, а ребенок слушать.

Еще лучше заставить марионетку сосчитать и присоединиться к ней дюйм.

Эту работу можно расширить и усложнить, если у детей это получается хорошо.Например, ребенок / дети и марионетка могут сказать альтернативные номера. Если марионетка говорит «один», ребенок / дети «два», марионетка «Три» и т. Д.

Кукла может сесть в круг детей и пустить их. Марионетка говорит «один», затем следующие дети — «двое», затем следующие «трое» и т. Д. Марионетки хороши только для того, чтобы их сфокусировать и заинтересовать. Чтобы узнать больше о 14 математических играх с куклами, ознакомьтесь с этой статьей. Куклы отлично подходят для всех видов деятельности со счетом

3.Подсчет песен, которые подсчитывают

Это может быть один из самых успешных способов начать дети уходят на путь механического счета.

Проблема с подсчетом песен заключается в том, что большинство они считают в обратном порядке. Это одна из странных загадок счета песен. Большинство из них придерживаются структуры «одним меньше». Есть такие песни, как Five Little Speckled Лягушки », или« Пять человечков в летающей тарелке », которые начинаются с пяти и затем получайте на один меньше с каждым стихом, который вы поете.

Это не та песня, которую нужно начинать детям механический подсчет.Им нужны песни, которые начинаются с единицы и идут вверх.

К счастью, они существуют!

Есть три хорошо известных примера этих типов песни.

Один — 1,2,3,4,5, «Однажды я поймал живую рыбу». Это здорово для того, чтобы дети считали до десяти.

Два других примера: 1, 2, Buckle My Shoe и 1 Potato, 2 Potato, 3 Potato, 4. Список из десяти примеров песен такого типа, которые можно считать, можно найти в этой статье.

Спой много таких песен детям, и их способность заучивать счет должна улучшиться.Музыка — отличный инструмент для получения дети очень интересовались и увлекались математикой.

4. Подсчет действий в повседневной жизни

Это, строго говоря, не механический подсчет, как вы собственно подсчет того, что существует. Однако это один из лучших способов заставить детей заучивать счет, и это определенно то, что я не мог оставить в стороне.

Все мы сталкиваемся с последовательностями чисел на протяжении всей жизни. Некоторые классические примеры, которые часто будут видеть дети, — это скалолазание или скалолазание. лестница.

Если считать вместе с ребенком каждый раз, когда взбираешься наверх лестницы, вы действительно закладываете отличный фундамент для механического счета.

Другими примерами являются такие вещи, как совместные прыжки и считать прыжки или хлопать и считать хлопки.

5. Подсчет объектов в повседневной жизни

Идея аналогична подсчету действий. На этот раз ты просто подсчитывают предметы, часто опять же просто в повседневных жизненных ситуациях.

Прекрасным примером этого являются такие вещи, как подсчет блоков, когда вы кладете их обратно в коробку.

Подсчет количества имеющихся у вас блюд, например количество моркови на вашей тарелке.

Или подсчитать, сколько у вас обуви.

Простое добавление подсчета в повседневную жизнь — отличная платформа для развития и консолидации механического подсчета. В моей статье о взаимном соответствии (и о лучших способах обучения этому) есть еще много примеров такого подсчета.

6. Счет по кругу

Это простая групповая игра, в которой участвуют все, и Надеюсь, это поможет очередности и сотрудничеству.

Один ребенок заводится, и они говорят «один». Затем следующий человек говорит «два». Продолжайте так по кругу.

Чтобы лучше сосредоточить их внимание, вы можете использовать предмет. Например, попросите их передать игрушку или марионетку. Только ребенок, который держит марионетку может говорить!

Чтобы расширить эту игру, вы можете попробовать много разных вещей. Получать например, использовать другой голос! Тогда они все будут считать, как привидения или инопланетяне! Это действительно воодушевляет.

Вы также можете сказать, что есть один номер, который им не разрешено сказать. Или произнесите глупое слово вместо числа, например, вместо того, чтобы сказать «шесть» скажите «сосиски» вместо «колбасы». Это развивает предвкушение, а также они смеются и наслаждаются этим.

7. Подсчет с партнером / взрослым

Эта игра похожа на игру по кругу. игра. Либо сядьте лицом к партнеру, либо к взрослому (в зависимости от того, как вы Это).

Один человек говорит «один», другой — «два», а затем вы просто продолжай так.

Когда вы подсчитаете, сколько сможете, попробуйте начать заново. с другим человеком, говорящим одно. Таким образом, вы можете сказать цифры, которые никогда не сказал первый раз.

Эти игры, в которых вы по очереди заставляете их задуматься, смотрите на своего партнера, слушайте и сразу же по очереди.

Разбудите его голосами персонажей или заставьте их пройти что-то между ними, когда они считают, например, плюшевый мишка или «счетный камень» (камень с нарисованными или нарисованными числами).

8. Подсчет в командах

Чтобы попробовать это, вам понадобится немало детей. Хватай их сидеть в двух «командах», одна команда смотрит на другую.

Хорошо работает, если есть что указать на команды когда настала их очередь говорить. Например, волшебная палочка хорошо подойдет для это.

Направьте волшебную палочку на первую команду, и они скажут «один».

Затем укажите на следующую команду, и они скажут «два». Вернуться к первые, которые говорят «три».

Продолжайте так.Это немного похоже на теннисный матч, с числа переходят от одной команды к другой. Продолжайте, насколько это возможно, помогая им, если требуется.

Чем больше вы будете выполнять все эти действия, тем дальше они будут уметь идти в долгосрочной перспективе.

9. Подсчет марта

Движение и математика идут рука об руку, и это занятие отлично подходит для этого. Движение помогает детям задействовать больше частей своего мозга, и обогащает любой учебный опыт.

Марширование — один из самых простых способов довести движение до механический подсчет.

Достаточно просто заставить всех детей встать, а затем начать марш. При первом марше говорят «один», на втором — «два» и так на. Они могут маршировать по комнате или снаружи, или они могут просто маршировать по место.

Штамповка аналогична. Мне нравится, когда они топчутся, как гиганты с сердитыми лицами! Вы можете топать и считать, используя голос своего гиганта.

Это занятие также закладывает основу для понимания странного и даже числа позже.

Вы будете топать одной ногой для четных чисел, а другой — для четных.Дети не узнают, что это происходит, но почувствуют закономерность. Позже опыт приведет к большему пониманию.

Эти игры были бы великолепны на открытом воздухе. Чтобы узнать больше о других играх, не относящихся к математике, прочтите эту статью — Математические игры на открытом воздухе — 50 действительно работающих идей!

10. Танцевальный счет

Теория танцевального счета аналогична. Поднимите их и двигаться, и дети будут реагировать более позитивно и помнить навыки лучше.

Включите качающуюся музыку. Это может быть что угодно с хорошим яркий ритм.

Затем выберите два простых танцевальных движения, которые можно выполнять одно за другим. другой. Например, можно бросить руки влево, а затем бросить ваши руки вправо.

Тогда начинайте считать по мере того, как вы делаете ходы! Бросьте руки к слева и скажите «один». Раскиньте руки вправо и скажите «два». Держать собирается.

Когда они зайдут так далеко, как смогут, выберите еще два движется, и начните с одного.

11. Подсчет действий

Движение также является ключевой частью этой идеи. Еще раз, как со многими из этих стратегий нет необходимости иметь какие-либо ресурсы или приготовить что угодно.

Вы просто выбираете действие, которое хотите попробовать, затем выполняете это действие и считать одновременно!

Например, действие может быть прыжком. Прыгай и считай!

Вы можете попробовать всевозможные движения, например подпрыгивание, кивание, прыжок, похлопывание по частям тела или мигание.

Это забавные вещи, и если детям нужно сосредоточиться на двух вещах сразу, кажется, это лучше работает в закреплении навыка механического счета.

12. Использование марионеток для пальцев

Это хорошо работает, если у вас достаточно марионеток для всех. детям, с которыми вы собираетесь заниматься этим занятием.

Попросите детей надеть марионетки на пальцы, а затем использовать их марионеточные голоса, чтобы считать в унисон. Если у вас много та же марионетка, тогда это будет звучать как припев этого голоса.Если у вас много мыши, например, все они будут озвучивать мышиные голоса.

Если у вас много разных персонажей для марионеток, вместо этого будет большая какофония голосов, объединенных воедино. Отлично подходит для весело считать!

13. Шепот, как шпионы

Дети любят шпионов и супергероев в ролевые игры, а что может быть лучше супер-шпионского подсчета!

Для этого одному ребенку нужен партнер (или, если вы родитель, тогда только вы и ваш ребенок будете партнерами).

Вы будете шептать числа друг другу, взяв поворачивается, чтобы сказать число.

Например, один ребенок шепчет «один», а другой — «два». Продолжайте так! Не позволяйте никому вас слышать!

Шпионский шепот — отличный способ научить многим стратегиям. В моей статье упоминается о хитрых словах и о 12 лучших играх, чтобы их научить.

14. Zoom Zoom Zoom Game

Они отлично подходят для механического счета, а также для обратный отсчет, а также следующий шаг.

Это игра супер кругов. С детьми в кружке, встаньте в середину круга и затем укажите на одного ребенка. Идея состоит в том, чтобы медленно ходите по кругу с вытянутым пальцем так, чтобы вы медленно указывая на каждого ребенка по очереди. Пока вы это делаете, дети наизусть счет — 1, 2, 3 и т. д.

Когда вы дойдете до 10, ребенок, на которого вы указываете, будет «космонавтом». Они должны встать и встать посреди круга — («ракеты»). Продолжать опять таки.

Когда вы выбрали 5 детей космонавтами, затем спойте песню Zoom Zoom Zoom:

Zoom Zoom Zoom

Мы идем на Луну!

Zoom Zoom Zoom

Мы будем там очень скоро!

5, 4, 3, 2, 1, 0 — Взлетать!

Затем все полетят в космос с максимально возможными звуковыми эффектами. Повторите игру еще раз, пытаясь найти новых космонавтов, если сможете.

Это одна из моих любимых игр с парашютом. Чтобы ознакомиться с полным ассортиментом, взгляните на эти 40 величайших игр с парашютом для детей.

15. Змея, считающая и прыгающая

Это немного похоже на конгу, оживленную еще больше с помощью прыгать и считать!

Встаньте в большую линию конги. Тогда либо все вместе прыгают вперед и скажите «один», или все сделают шаг в сторону и скажут «один». Затем прыгните или сделайте шаг в другую сторону и скажите «два». Продолжать!

Отлично на улице, где можно быть шумным и хриплым как вы, возможно, захотите.

Отличное занятие для совместной работы и помощи друзьям чтобы все работали вместе.

16. Splat The Playdoh

Математика для Playdoh — одна из самых совершенных форм, чтобы увлечь детей и заинтересовать их числами.

Эта игровая площадка — одна из самых лучших.

Что вам нужно, так это туф или большой поднос, который можно поставить на столе. Затем попросите того, кто занимается этим делом, сделать жребий и много маленьких шариков playdoh.

Идея состоит в том, что ребенок шлепнет один мяч в пластилин и скажет «один».Затем следующий, введите «два» и продолжайте так. Если хотите, они могут использовать что-нибудь для разбрызгивания, например мухобойку или небольшой удобный для детей молоток.

Продолжайте брызгать и считать!

Одновременно могут заниматься несколько детей, или один ребенок может заниматься шаг, затем следующий и т. д.

17. Хлопания и счет

Хороший простой способ закончить, но один из лучших способов Практика механического счета заключается в том, чтобы хлопать в ладоши одновременно со счетом.

Считай и хлопай! Это так просто.

Чтобы усложнить задачу, вы можете попробовать такие вещи, как счет в другой голос и хлопки одновременно. Или вы можете шептать, как шпион, и хлопать.

Все, что угодно, чтобы сделать его увлекательным и оживить счет!

Заключение

Удачи в этом механическом подсчете!

Механический счет — одна из основ математики, а важная основа для развития детей. Тем не менее, это определенно весело и простая вещь для обучения, на самом деле не требующая какой-либо работы или подготовки.

Маленькие и частые способы сделать это! Чем больше вы заставите их считать, тем лучше и увереннее они станут.

Если вы нашли эту статью полезной, то почему бы не взглянуть на одну из следующих:

Считайте до 100: стратегии и мероприятия

Привет! Я вернулся, чтобы поделиться учебными стратегиями и заданиями, чтобы научить учащихся начальных классов, как заучивать счет до 100. Как всегда, продолжайте читать, чтобы получить бесплатное задание для ваших математических центров или обучение в небольших группах!

Давай поговорим о счете!

Счетчик — один из самых важных или самых важных навыков, которым нужно заниматься с учениками начальной школы.Умение механически подсчитывать — это навык, который нужен учащимся, прежде чем они смогут развить мощность множества и прежде, чем они смогут освоить более сложные навыки, такие как составление и разложение чисел и… глоток… числовое значение.

Подсчет относится к знанию того, какие числа идут следующими в последовательности. Это звучит просто, но механический счет может быть затруднен при первом изучении.

Некоторые препятствия, мешающие учащимся успешно считать:

1. Пропуск чисел или неправильное произнесение числа (особенно запутанные числа для подростков)
2.Невозможно сосчитать по десятилетиям (от 9 до 10, от 19 до 20, от 29 до 30 и т. Д.)
3. Невозможно рассчитывать от числа, отличного от 1 (начиная с 15, а затем повторяя 16, 17, 18 и т. Д.).

Вот и хорошая новость: все эти препятствия на пути к механическому подсчету можно успешно устранить с помощью прямых, четких инструкций и множества возможностей с использованием различных средств практики.

Простые математические процедуры, помогающие ученикам наизусть считать

Практикуйтесь в счете каждый день! Предложите ученикам считать, петь, танцевать и считать вместе с другом.На YouTube есть ТОННА бесплатных видео с подсчетом. Мои студенты любят Джека Хартмана, который считает видео. Щелкните здесь, чтобы посмотреть несколько его видео. Если ваш округ блокирует видео на YouTube, вы можете придумывать свои собственные танцевальные движения.
Научите студентов замечать закономерности — Используя таблицу 100, попросите студентов рассказать о том, что они замечают в расположении чисел. Они могут заметить, что он следует шаблону 0-9 или что каждый столбец имеет одинаковый номер. Попросите учащихся рассказать о закономерностях, которые они замечают, записать, что они говорят, и поделиться своими выводами с классом.
Сколько дней мы учимся в школе? — Это отличная практика для ежедневного счета до 100! Ученики добавляют соломинку (или то, что вы используете) каждый день, чтобы обозначить, сколько дней они были в школе. Каждый раз, когда они набирают 10, они связывают соломинки. В 100-й день школы устройте вечеринку с математической тематикой!
Подсчет календаря — Числа от 1 до 31 непростые! При обучении детей механическому счету я рекомендую в первую очередь сосредоточиться на числах от 1 до 31. Вы можете использовать календарь каждый день, чтобы практиковаться в написании чисел, говоря, какие числа идут до и после, и подсчитывая, сколько дней осталось до особого события.Вы также можете перемещать числа в неправильном месте и просить учащихся найти число, которое находится в неправильном месте.
Считайте по кругу — Попросите учащихся сосчитать или сосчитать по кругу. Каждый ученик называет следующее число. Помните, не всегда начинайте с 1! Используйте карточки с цифрами, чтобы выбрать номер для начала. Если это начало года, я бы ограничил диапазон числами от 1 до 31.

Это действия, которые вы можете выполнять каждый день как часть своей математической рутины.

Упражнения для обучения студентов счету

Вот несколько заданий, которые вы можете использовать, чтобы дать вашим ученикам дополнительную практику для механического счета до 100!

Партнерские счетные карты

Лучший способ научиться механизировать счет — это считать! Это упражнение можно использовать в небольшой группе или целой группой. Вы выбираете карточку, или студент выбирает карточку, и они рассчитывают от этого числа, пока не достигнут целевого числа. Это отличный способ дифференциации и расширения диапазона чисел в зависимости от навыков вашего ученика.Например, если ученик работает над механическим счетом до 25, используйте счетные карточки до 25.

Карты с отсутствующими номерами

Студенты, которые пропускают числа при подсчете, выиграют от отсутствия карточек для подсчета чисел. Студенты считают и записывают недостающее число. Попросите их объяснить, откуда они знают, что номер отсутствует (т. Е. Они посмотрели на шаблон или знают, что идет до или после).

Чтение и запись

«Чтение и запись» — отличный способ научить учеников правильно считать и писать числа.Для учащихся этого возраста с точки зрения развития уместно иметь некоторые перевернутые буквы, но это не значит, что вы не можете дать им опыт, который поможет им правильно формировать числа. Для этого задания учащиеся выбирают, читают и записывают заданное число. Они могут использовать числовую полосу в верхней части страницы, чтобы помочь им правильно формировать буквы. Он начинается с 2, поскольку большинство студентов умеют писать 1.

Отжим и крышка

Spin and Cover — отличный способ научить студентов читать числа до 100.Они крутят обе блесны, пишут число и закрывают число на 100-й диаграмме. Это интересный способ познакомиться с паттернами на графике 100.

Рассчитывай или вернись!

Что отличает ваши лучшие счетчики чисел от ваших развивающихся счетчиков чисел? Лучшие счетчики чисел знают, какое число стоит до и после целевого числа. У них сильные навыки владения числами. Студенты выбирают карточку и пишут, что стоит до и после этого числа.В зависимости от того, какую карточку вы выберете, студенты также могут отсчитывать от заданного числа.

Пазлов!

Кто не любит большие головоломки? Студенты сравнивают цифру с изображением. Это забавное занятие для тренировки счета на десятки.

Сколько пальцев?

Счетчик пальцев — очень важный навык в этом раннем возрасте. Почему? Ваши 10 пальцев — это, по сути, десять кадров! Вы можете использовать свои пальцы, чтобы складывать и вычитать, и рассчитывать на них! НО сейчас мы будем использовать пальцы, чтобы считать от десятков до 100.Учащиеся выбирают карточку с цифрой и показывают пальцами карточки, сколько.

Путешествие к 100!

Это отличная партнерская игра! Студентам нужен жетон, чтобы перемещаться по настольной игре. Студенты бросают кубик и перемещают столько мест на доске. Затем они говорят, какие числа идут до и какие после. Есть 2 дифференцированные настольные игры. Студентам, которым может потребоваться помощь со счетом, вы можете предоставить им таблицу 100.

Рулон и крышка

Я люблю игры с роликами и обложками! Их так просто объяснить, но они имеют большую обучающую ценность.Учащиеся бросают кубик, выбирают и читают число в столбце этого числа. После того, как они его прочитают, они его закрывают. Это может быть независимая или совместная игра.

Что будет дальше?

Это партнерская деятельность. Студент выбирает карточку, читает числа и говорит, что будет дальше. Если их ответ правильный, переместитесь на одну клетку. Затем наступает очередь другого игрока. Побеждает тот, кто первым придет к финишу.

Что между ними?

Это отличная партнерская игра, которая помогает научиться легко распознавать числа.Студент берет карточку, читает числа и говорит, какое число находится посередине. Если они правы, они перемещаются на 1 деление. Затем наступает очередь другого игрока.

Что будет дальше?

Учащиеся раскручивают счетчик и записывают следующие 3 числа. Это отличное занятие для обучения студентов счету на десятилетия.

Что будет дальше?

Помните, я упоминал, что студентам сложно считать десятилетия? Вот ДРУГОЕ занятие, чтобы дать им возможность самостоятельно попрактиковаться.Студент бросает кости, читает числа в ряду и закрывает следующее число с помощью манипулятора. Это увлекательное занятие самостоятельно или с партнером. Есть и игра на счет десятками!

Что отсутствует? Игра №2

Это действие карточки задачи. Учащиеся выбирают карточку с заданием и записывают недостающее число, считая от заданного числа. Они записывают недостающий номер на регистрационном листе.

Запись и стирание

Студенты берут карточку и записывают недостающие числа на доске.

Выберите и запишите

Студенты берут карточку и записывают следующие несколько чисел в числовую строку. Они могут записать ответ на карточке или на доске.

Гигантские счетные карты

Ученики расставляют карточки с номерами в порядке от 1 до 100 или от 10 до 100. Это отличное упражнение для партнеров, позволяющее заучивать до 100.

Рабочие листы

Студенты практикуются в написании и чтении чисел до 100.

Есть ли у вас какие-нибудь упражнения, которые вы используете, чтобы научить своих учеников механически считать до 100? Дайте мне знать в разделе комментариев ниже.

Загрузите бесплатные карты для подсчета пальцев, щелкнув ссылку ниже:

Вам нравится этот ресурс? Вы можете приобрести это здесь?

Счастливого обучения!
Тройник!

Семь лучших способов научить счету до 100

Этот пост может содержать партнерские ссылки. Пожалуйста, прочтите мое заявление о раскрытии информации для получения более подробной информации.

Если вы подписаны на меня в Instagram (@raisingdavinci), вы, возможно, видели, как я писал о том, что мы начали знакомить нашего трехлетнего ребенка с числовым значением 100.Мы не торопились с десятками и пытались научить его разными способами вместе с его математической программой (Math-U-See)

Вот 7 наших любимых способов научиться считать от 1 до 100.

# 1
Считаем все. Я знаю, что это настолько очевидно, но это действительно имеет значение: мы считаем шаги, мы считаем машины, мы считаем дома, когда едем, мы считаем, просто чтобы иногда сосчитать. Я думаю, что это действительно помогло ему учиться, он все еще понимает некоторые из девяток (39,49,59 и т. Д.), И нам нужно напоминать ему, что будет дальше.

# 2
Я нашел эту песню на YouTube, и она мне очень понравилась. Видео хорошее, но мы часто поем эту песню. Естественно, будучи ребенком 90-х, я тоже танцевал!

# 3
Бесконечные числа приложение. Обожаю это приложение! (Мне действительно нравятся все приложения Originator) Бесплатная версия — это номера 1-10, но когда вы платите за полную версию, вы получаете номера 1-100! Это отличный способ закрепить заучивание чисел.Я позволял ему играть на iPad или на моем телефоне в качестве особого удовольствия, когда мы ходили в магазин за продуктами или в тихое время.

# 4
Пропустить счет по 10. Это действительно простая игра. Мы использовали листы пенопласта, которые я купил в долларовом магазине, чтобы сделать их более прочными.

# 5
Книги! Вот наши фавориты!

# 6
100 мешков.Это постоянный урок. Мы начали с фасоли, а на следующей неделе — попкорн, а затем — семена чиа. Да, семена чиа. Поскольку они такие крошечные, это отличный способ показать, что 100 единиц одного объекта кажутся большим количеством, а 100 единиц другого — не очень большим количеством! Я люблю спрашивать его, сколько в сумке, по его мнению, 100 XYZ, прежде чем мы ее наполним. Начать действительно просто — вы просто пересчитываете 100 штук и кладете в сумку. Вот несколько идей для начала: пенни, ватные шарики, рис, семена, бобы, чирио….пр.

# 7
Приводим числа по порядку. Я люблю эту сетку Монтессори 1-100!

Какие из ваших любимых способов? Дайте мне знать ниже!

Связанные

Как учить детей числам от 1 до 10

Стимулирующие и эффективные способы обучения детей основам чисел.

Студенты почему-то любят считать. Это удачно, потому что числа являются основной частью курса почти любого молодого учащегося, начиная со счета до пяти или десяти и заканчивая деньгами, датами, временем и прочим.Эта статья о ранних стадиях этого процесса, в том числе о том, чтобы сделать эту бесконечно повторяемую тему всегда новой и интересной. Большинство действий и советов, приведенных ниже, также работают с более высокими числами, например до двадцати или до ста десятками.

Семь этапов обучения этим числам:

Считаем до 10
Отсчет от 10 до 1
Считаю вещи
Понимание и реакция на произнесенные случайные числа от 1 до 10
Умение произносить случайные числа при отображении числа
Распознавание чисел, записанных в виде слов, и реагирование на них, e.грамм. распознавание числовых слов, распознавание формы слова и распознавание определенных ключевых букв. (Распознавания первой буквы недостаточно, есть две цифры, начинающиеся с T, и две, начинающиеся с F.)
Умение писать числа

Приведенные ниже обучающие идеи более или менее следуют порядку, указанному выше.

Счетчик вверх и вниз

Лучшие занятия для этого — те, которые вовлекают детей и чьи действия и т. Д. Дают им некоторое подкрепление размером числа, которое они слышат или говорят.Самый простой способ сделать это — становиться все громче и громче при подсчете, а затем все тише и тише при обратном отсчете. Это можно комбинировать с действиями в «Growing Numbers», упражнении TPR, в котором они начинают приседать с опущенной головой и руками на коленях для «1» и становятся все больше и больше по мере подсчета, пока не окажутся вытянутыми высоко. для «10». Шаги назад и вперед по мере их подсчета также работают таким же образом. Есть также множество сборников рассказов и песен для счета вверх и вниз, например.г:

Пять маленьких обезьянок прыгают на кровати
Пять маленьких уток вылетели однажды
Десять индейцев
One Little Finger (Tap Tap Tap)
Десять зеленых бутылок на стене
Десять лежали в постели (и Малыш сказал, что перевернулся)

Настоящих игр для счета от 1 до 10 не так много, но учитель может преждевременно остановиться или сделать ошибку и заставить учеников исправить их.В качестве альтернативы они могут добавить еще одну задачу, из-за которой ученикам будет труднее получить от 1 до 10, например им нужно бросать мяч вперед и назад, не касаясь земли, когда они считают, или считать, когда они складывают блоки, чтобы построить башню. Вы также можете закончить все классные игры, когда одна команда наберет десять очков, и попросить класс подсчитать очки, прежде чем они перейдут к следующему занятию.

Считаю вещи

Есть много игр, в которых ученики считают, сколько чего-то есть.Ученикам лучше всего посчитать то, что находится вокруг них в классе. Это будет веселее и активнее, если вы попросите их бегать и трогать предметы, пока они их считают, в ответ на вопросы типа «Сколько там окон?» Вы можете добавить к этому интеллектуальный вызов, наполовину спрятав некоторые вещи (например, степлеры и коробки с мелками) по комнате. Эту идею сокрытия можно также использовать, когда учащиеся сидят, используя подробную картинку в стиле «Где Уолли», на которой учащиеся должны мчаться, чтобы определить «Сколько жирафов там?» внимательно присмотревшись к нему.Гораздо более простой вариант — учитель показывает карточку с несколькими предметами, чтобы ученики могли посчитать и выкрикнуть их как можно быстрее.

Подсчет песен также можно использовать на этом этапе, если вы используете песни, в которых учащиеся могут выбрать число, например для выбора таких людей, как Жевательная резинка, жевательная резинка в блюде (Сколько штук вы хотите?) .

Ученики также могут бегать, чтобы попрактиковаться в подсчете различных чисел, когда учитель говорит им, сколько вещей им следует искать, и просит их потрогать, когда они их считают, e.грамм. «В этой комнате пять человек. Кто они такие?»

Случайные числа

Хотя затем они переходят к счету, последние две идеи, представленные выше, уже предполагают, что учащиеся производят числа или реагируют на них без обязательного предварительного счета. Во всех играх, представленных ниже, они также могут считать на пальцах и т. Д., Но обнаружат, что обучение, которое не нужно делать, увеличит их скорость и, следовательно, шансы на победу.

Самые простые игры — это игры, в которых учитель называет число, а ученики каким-то образом отвечают, например:

Бег и касание фигуры на стене
Бег и прыжок на фигуру, прикрепленную к полу
Бегущий и обводящий эту цифру или количество элементов на доске
Взять и показать карточку с фигурой на ней
Поднимая столько пальцев
Держа столько пальцев между своей группой (каждый должен держать хотя бы один)
Держа столько оружия среди своей группы
Удерживая столько предметов
Рисование такого количества объектов, например.грамм. оружие на монстра
Написание этой цифры
Создание этой фигуры, например из карандашей, скрепок, пластилина или их тел
Раскрашивание многих вещей в цвет, который говорит учитель, например «Цвет семь туфель синий»

Чтение чисел от 1 до 10

В большинство вышеперечисленных игр можно играть, когда учитель держит слово, пишет или указывает на слово, а не выкрикивает его. Бросок кубика с написанными числами — хороший вариант этого.Учитель также может показывать формы слов, медленно писать слова или показывать слова только с важными буквами (например, F и O для 4).

В качестве альтернативы, учитель все еще может выкрикнуть номер, но попросить учеников сделать что-нибудь с письменным номером, например возьмите правильное написанное число, бегите и ударьте по стене карточку с правильным написанным числом или бегите и обведите правильное написанное слово на доске.

Запись чисел от 1 до 10

Учащиеся могут реагировать на выкрикиваемое слово, неполное написанное слово, неправильно написанное слово, форму слова, фигуру, показ нескольких предметов или просьбу пересчитать количество предметов.Учащиеся могут соревноваться, чтобы добавить пропущенные буквы, исправить ошибки, написать слово с помощью магнитных букв или карточек с буквами или переставить перепутанные буквы.

6 стратегий обучения счету пропусков

Давайте поговорим о подсчете пропусков! Этот навык иногда рассматривается как произвольный математический навык или как то, что вы произносите на игровой площадке. Подсчет пропусков — это гораздо больше. Он помогает ученикам видеть закономерности в числах, а также закладывает отличную основу для понимания чисел и изучения фактов умножения.

1. ИСПОЛЬЗУЙТЕ КАЛЬКУЛЯТОР

Учителя обычно не думают об использовании калькуляторов, когда тренируются в счетчике пропусков. Однако они могут быть забавным и полезным инструментом при обучении этому навыку.

Совет учителя:

Покажите своему классу, как изменить начальное число, продолжая нажимать знак равенства (Пример 8 + 2 =, =, =, =). Соедините студентов с партнером.Один партнер указывает новую сумму до того, как другой партнер нажмет кнопку =. Они по очереди пытаются назвать следующий номер перед нажатием кнопки. Это весело для детей, потому что это соревнование, и эта стратегия помогает развить беглость чисел.

2. ИГРАТЬ В ИГРУ

Детские игры ЛЮБОВЬ! Это очень простая игра, в которую дети могут поиграть, чтобы научить детей счету без пропусков. Попросите учащихся сесть или встать в круг. Учитель начинает со случайного числа и заставляет учеников пропускать счет с этого числа, пока они не пройдут весь круг.

Совет учителя:

Самое лучшее в этой игре то, что вы можете модифицировать ее в соответствии со своими потребностями. Например, чтобы сделать его более высоким, начните с числа, которого нет в обычной последовательности подсчета пропусков. Например, вместо того, чтобы просто пропускать счет по двойкам (например, 2, 4, 6, 8 и т. Д.), Начните с нечетного числа и пропустите счет по 2 секунды (например, 7, 9, 11, 13 и т. Д.) Или пропустите считайте нетрадиционными числами, такими как 7 или 9.

3. ОПРОС

Иногда ставится под сомнение та стратегия обучения, которую часто упускают из виду.Вы можете задать множество вопросов, которые заставят ваших детей критически задуматься о пропуске счета. Например, чаще всего студентов просят сделать «Пропустить счет на 2», попробуйте спросить: «Сколько способов вы можете сосчитать до 36?» Вместо того, чтобы просить учеников сосчитать до 50 на 10, спросите: «Можете ли вы сосчитать до 50 на 11? Почему или почему нет?»

Ознакомьтесь с моими математическими карточками со счетом пропусков и четными / нечетными числами. Они отлично подходят для того, чтобы задавать вопросы всей группе или небольшой группе.

4. ИСПОЛЬЗУЙТЕ КЛЕЙКИЕ ЗАМЕТКИ С ДИАГРАММОЙ 100 секунд

Использование стикеров может быть очень увлекательным и интерактивным способом попрактиковаться в подсчете пропусков. Одним из примеров может быть использование увеличенной числовой таблицы и наклеивание определенных чисел липкой записью. Напишите по одной букве алфавита на каждой наклейке. Затем попросите учащихся записать недостающие числа на отдельном листе для записей. В приведенном ниже примере попросите учащихся начать с цифры 9 и пропустить счет на 3 секунды.

Если вам нравятся стикеры, обязательно ознакомьтесь с моим постом «10 способов научить математику с помощью заметок Post It».

5. ПОЙТЕ ПЕСНИ

Все мы знаем, что дети любят песни. Существует так много бесплатных ресурсов о подсчете пропусков, которые позволят вашим детям одновременно двигаться и обучать математике. Посмотрите один из моих любимых ниже:

Пропустить счет (… а затем добавить) от Harry Kindergarten Music — Harry Kindergarten Music содержит отличные музыкальные видеоклипы, которые включают в себя ряд навыков и концепций.Это видео с подсчетом пропусков имеет отличные визуальные эффекты. Он показывает, как пропустить счет, используя базовые десять стержней, а затем добавляя единицы, чтобы вычислить общую сумму. Это отличный инструмент для концептуального обучения математике!

6. ИСПОЛЬЗОВАНИЕ МАНИПУЛЯТОРОВ

Студенты чувствуют себя очень успешными, когда они могут считать по 2, 5, 10 и т. Д. Но будьте осторожны! Может показаться, что учащиеся понимают стратегию, потому что они могут повторять последовательность чисел, но действительно ли они понимают цель пропуска счета? Вытащите манипуляторы.Используйте кубики-оснастки, конфеты. скрепки или любые другие предметы, которые вы можете найти.

Обязательно задавайте наводящие вопросы, например: 1) Что вы заметили? 2) Как меняется сумма? или 3) Если вы продолжите этот шаблон, каково будет общее количество объектов в 10-й, 11-й или 12-й модели?

Нажмите на фото ниже, чтобы ознакомиться с информативным постом из Уголок тренера по математике о том, почему нам все еще нужно использовать эти конкретные объекты при внедрении этого математического навыка.

Есть ли у вас другие способы обучения счету пропусков в классе? Пожалуйста, поделитесь в комментариях.

Преподавание математических понятий — навыки индивидуальной переписки и счета

Индивидуальная переписка и навыки счета

В дополнение к концепциям, обсуждаемым в разделе об основных концепциях, понимание взаимно однозначного соответствия объекта объекту также необходимо, прежде чем ребенок сможет выполнять осмысленный подсчет и более высокие вычисления.

В повседневной жизни дети могут найти множество возможностей для индивидуальной переписки.Они могут поместить один носок внутрь одного ботинка или один ботинок на одну ногу; они могут получить по одной салфетке или закуске для каждого члена семьи или класса; на каждую из нескольких емкостей можно по одной крышке; они могут складывать кусочки в цельные пазлы.

Как только дети поймут эти отношения, они могут связать одно число с одним предметом, а затем с пониманием считать. «Механическое запоминание набора чисел бессмысленно» (Мур, 1973, стр. 67), а счет — это навык, на который не следует подчеркивать, пока ребенок не продемонстрирует понимание базовой классификации, сохранения, сериализации и сравнения наборов в обоих качествах. уровень (атрибуты объектов) и уровень количества (общие суммы в группах или наборах).

Когда учащиеся будут готовы развить навык счета, они могут извлечь пользу из изучения нескольких стратегий счета, чтобы повысить их точность и эффективность. Иногда учащиеся самостоятельно разрабатывают одну или несколько таких стратегий, но им выгодно проводить обучение в этой области. Как и в случае с любыми концепциями или навыками, важно начать работать с реальными объектами и манипуляторами и продолжать использовать их в качестве учебных пособий.

Подлежащие подсчету объекты часто находятся в одном из нескольких типов массивов: линейных, круглых, прямоугольных или случайных.Следующие ниже шаги могут быть полезны маленьким детям для определения ситуации подсчета, ее организации и отслеживания их прогресса при подсчете элементов в массиве.

Сканирование. Ребенок перемещает руки по верхней части каждого элемента в массиве, который нужно подсчитать, чтобы получить информацию об объектах и общем поле, по которому они расположены. Ребенок также мог брать и исследовать предметы и класть их в лоток.
Организация — Если предметы отображаются случайным образом, ребенок может переместить все предметы в одну сторону для подготовки к подсчету.Если элементы уже расположены линейно, ребенок может найти первый элемент в серии и отсканировать, чтобы подтвердить расположение.
Разделение на разделы — ребенок может подсчитывать отдельные предметы и перемещать подсчитанные предметы в отдельную область на лотке. Ребенок также может брать предметы по одному, давать им имена и заменять их отдельно от тех, которые еще предстоит пересчитать. Ребенок также может индивидуально коснуться каждого предмета для подсчета одной рукой, давая каждому числовое имя, в то время как другая рука отслеживает следующий предмет для подсчета.

При обучении навыкам счета эти советы могут помочь:

Объедините словесные задачи с вычислениями на самых ранних уровнях, даже если они включают в себя только простой устный «рассказ», который сопровождает подсчет наборов.
Как можно скорее свяжите использование манипуляторов, устного счета и числовых выражений с отображением этих чисел на бумаге с помощью брайлера и на счетах. Используйте манипуляторы вместе с этими инструментами при переходе к брайлеру и счетам.
Обеспечить учащегося заметками об основных понятиях чисел; их можно упростить с помощью примеров для иллюстрации. Небольшой флип-чарт, например те, что продаются в магазинах для учителей, можно пометить шрифтом Брайля.
Модифицируйте брайлевскую метку, накрыв ее прозрачным брайлоном; перемаркируйте его на 0 посередине, 0-50 вправо и отрицательные числа влево. Аналогичная модификация может быть сделана для линейной линейки с выступом.

Занятия по обучению счету

Попросите ребенка сравнить / сопоставить / отсортировать группы объектов в наборы; затем попросите его или ее определить количество предметов в каждом наборе, обозначив их по имени и с помощью некоторого шаблона (например,(например, хлопать в ладоши или звонить в колокольчик столько же раз, сколько указано в наборе).
Используйте счет песен и игры пальцами, чтобы попрактиковаться в счете вперед, назад, по двойкам, по пятеркам, по десяткам и т. Д.
С помощью брайлера попросите учащегося сосчитать места, чтобы добраться до звонка, начиная с разных точек на линии; студент также может нажимать полные ячейки, чтобы соответствовать определенному числу.
Попросите ребенка вслух считать предметы, когда он или она по отдельности бросает их в контейнеры; начните с того, что бросайте по одному предмету за раз, затем по два за раз и так далее.
Отслеживание результатов игры может быть мотивирующим и актуальным способом применения навыков счета. Например, ребенок может подсчитать количество очков, заработанных людьми в карточной игре или в игре с мячом.
Запишите на пленку конкретные указания для самостоятельной практики студента. Например, используя поднос с разделителями, ученик может разместить определенное количество предметов в первом разделе, другое количество предметов во втором разделе и так далее. Студентов также можно попросить поместить карточку с правильным символом Кодекса Немета в каждую из секций, чтобы соответствовать количеству предметов.
Проведите «охоту за мусорщиком». Сообщите ребенку расположение нескольких контейнеров с объектами (в зависимости от памяти учащегося, ему можно указать одно местоположение за раз или сразу несколько). Дочерний должен пойти в места, получить контейнер с объектами, подсчитать количество в контейнере, а затем расположить контейнеры в правильной числовой последовательности. Затем ученик может пересчитать все предметы для получения общей суммы.
Используйте «говорящий планшет» с наложениями, содержащими ряды осязательных точек и фигур; запрограммируйте устройство, чтобы оно произносило количество фигур последовательно слева направо или сверху вниз.Ребенок прикасается к фигурам в правильной последовательности и получает подкрепление в соответствии с порядковым номером. Ребенок должен подтвердить правильную последовательность нумерации (подходит для учащихся с ограниченной мелкой моторикой).
Разработка автобиографической временной шкалы (в сотрудничестве с семьей ученика) требует, чтобы ученик на самом деле последовательно планировал важные события.