Как решить правильно задачу по математике: примеры и способы решения математических задач для родителей

примеры и способы решения математических задач для родителей

На протяжении всего обучения школьникам приходится решать задачи — в начальной школе по математике, а затем по алгебре, геометрии, физике и химии. И хотя условия задач в разных науках отличаются, способы решения основаны на одних и тех же логических принципах. Понимание того, как устроена простая задача по математике, поможет ребёнку разработать алгоритмы для решения задач из других областей науки. Поэтому учить ребёнка решать задачи необходимо уже с первого класса. 

Нередки случаи, когда точные науки вызывают у детей сопротивление. Видя это, учителя и родители записывают таких детей в «гуманитарии», из-за чего они только укрепляются во мнении, что точные науки — это не для них. Преподаватель математики Анна Эккерман уверена, что проблемы с математикой часто имеют исключительно психологический характер:

‍Детям вбивают в голову, что математика — это сложно. К длинным нудным параграфам в учебнике сложно подступиться. Учитель ставит на ребёнке клеймо «троечника» или «двоечника». Если не внушать детям, что они глупые и у них ничего не получится, у них получится ровно всё.

Чтобы ребёнку было интересно учить математику, он должен понимать, как эти знания пригодятся ему, даже если он не собирается становиться программистом или инженером.

Математика ежедневно помогает нам считать деньги, без умения вычислять периметр и площадь невозможно сделать ремонт, а навык составления пропорций незаменим в кулинарии — используйте это. Превращайте ежедневные бытовые вопросы в математические задачи для ребёнка: пусть польза математики станет для него очевидна. 

Конечно, найти в быту применение иррациональным числам или квадратным уравнениям не так просто. И если польза этих знаний вызывает у подростка вопросы, объясните ему, что с их помощью мы тренируем память, развиваем логическое мышление и остроту ума — навыки, в равной степени необходимые как «технарям», так и «гуманитариям». 

Как правильно научить ребёнка решать задачи

Если ребёнок только начинает осваивать навык решения задач, приучите его придерживаться определённого алгоритма.    

1. Внимательно читаем условия  

Лучше вслух и несколько раз. После того как ребёнок прочитал задачу, задайте ему вопросы по тексту и убедитесь, что ему понятно, что вычислять нужно количество грибов, а не огурцов. Старайтесь не нервничать, если ребёнок упустил что-то из вида. Дайте ему разобраться самостоятельно. Если в условиях упоминаются неизвестные ребёнку реалии — объясните, о чём идёт речь.

Особую сложность представляют задачи с косвенным вопросом, например:

«Один динозавр съел 16 деревьев, это на 3 меньше, чем съел второй динозавр. Сколько деревьев съел второй динозавр?». Невнимательно прочитав условия, ребёнок посчитает 16−3, и получит неправильный ответ, ведь эта задача на самом деле требует не вычитания, а сложения.        

2. Делаем описание задачи

В решении некоторых задач поможет представление данных в виде схемы, графика или рисунка. Чем ярче сложится образ, тем проще будет его осмыслить. Наглядная запись позволит ребёнку не только быстро разобраться в условиях задачи, но и поможет увидеть связь между ними. Часто план решения возникает уже на этом этапе. 

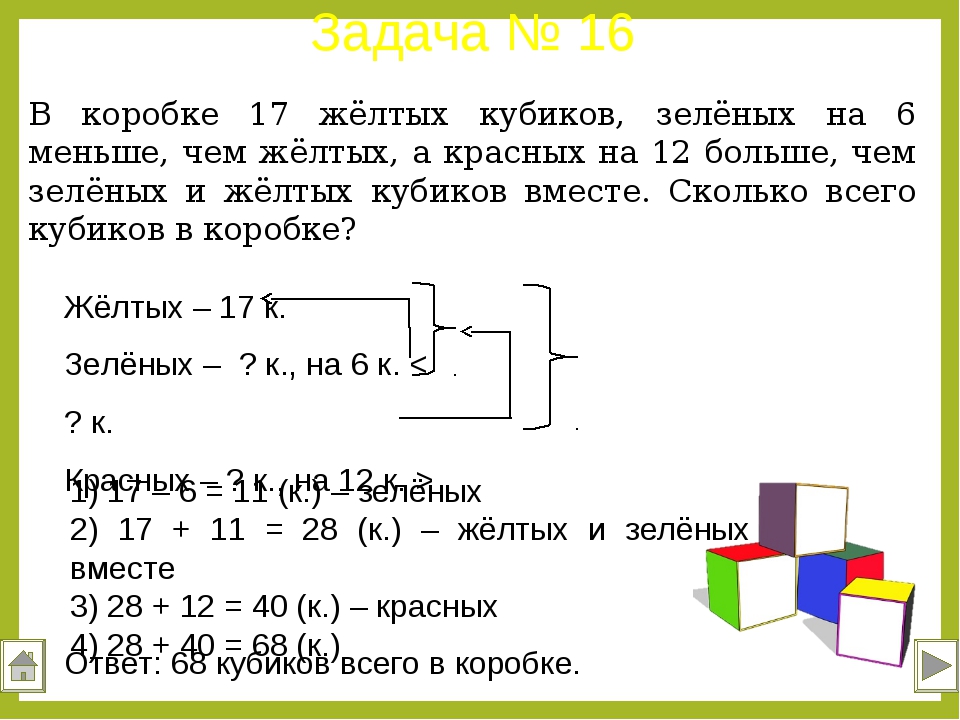
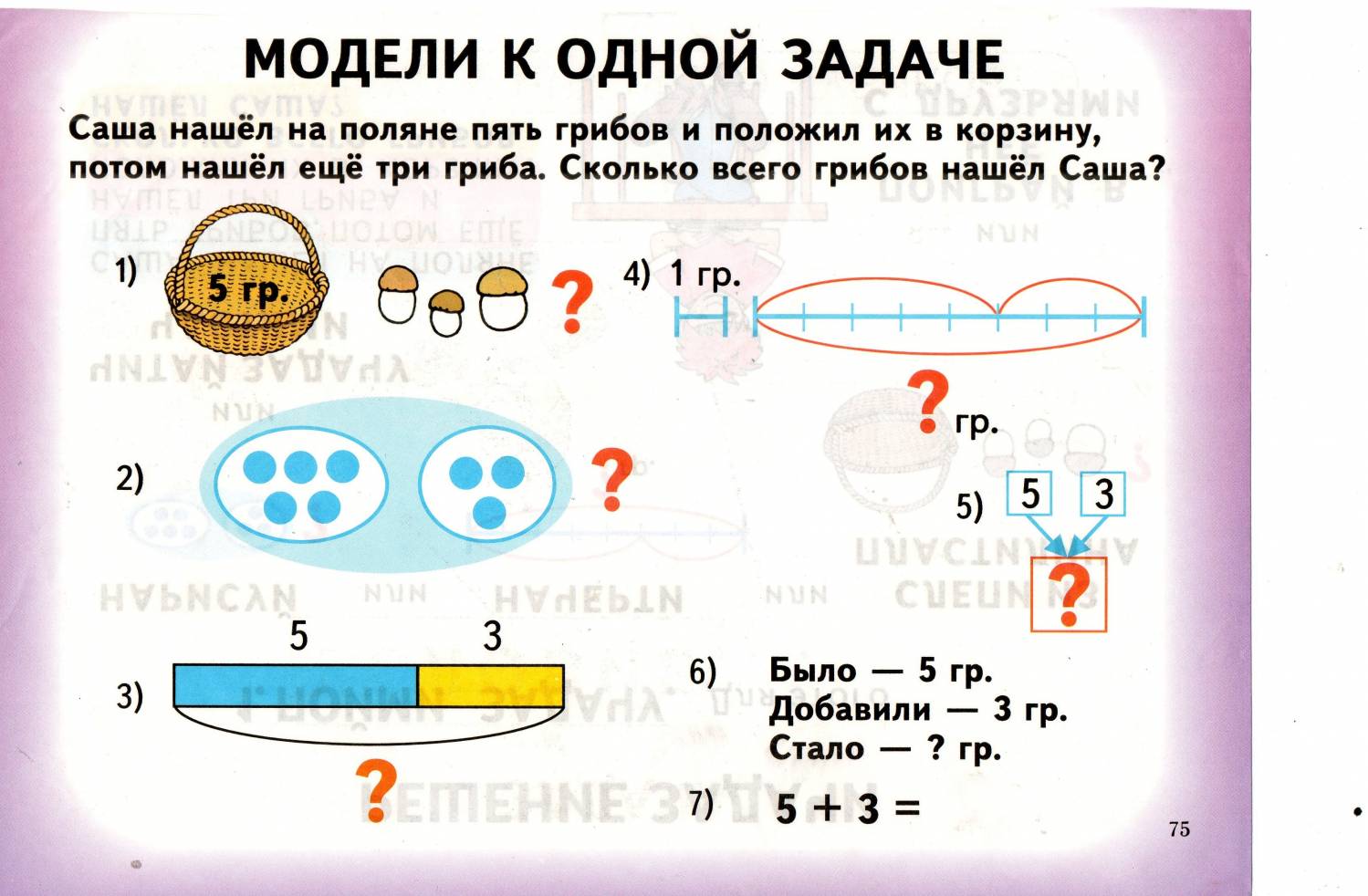
Ребёнок должен чётко понимать значения словесных формул и знать, какие математические действия им соответствуют.  

Формы краткой записи условий задач / shkola4nm.ru
‍

3. Выбор способа решения

Наглядно записанное условие должно подтолкнуть ребёнка к нахождению решения. Если этого не произошло, попробуйте задать наводящие вопросы, проиллюстрировать задачу при помощи окружающих предметов или разыграть сценку. Если один из способов объяснения не сработал — придумайте другой. Многократное повторение одного и того же вопроса неэффективно. 

Все, даже самые сложные, математические задачи сводятся к принципу «из двух известных получаем неизвестное». Но для нахождения этой пары чисел часто требуется выполнить несколько действий, то есть разложить задачу на несколько более простых. 

Ребёнок должен знать способы получения неизвестных данных из двух известных:

• слагаемое = сумма − слагаемое
• вычитаемое = уменьшаемое − разность
• уменьшаемое = вычитаемое + разность
• множитель = произведение ÷ множитель
• делитель = делимое ÷ частное
• делимое = делитель × частное
  

После того как план действий найден, подробно запишите решение.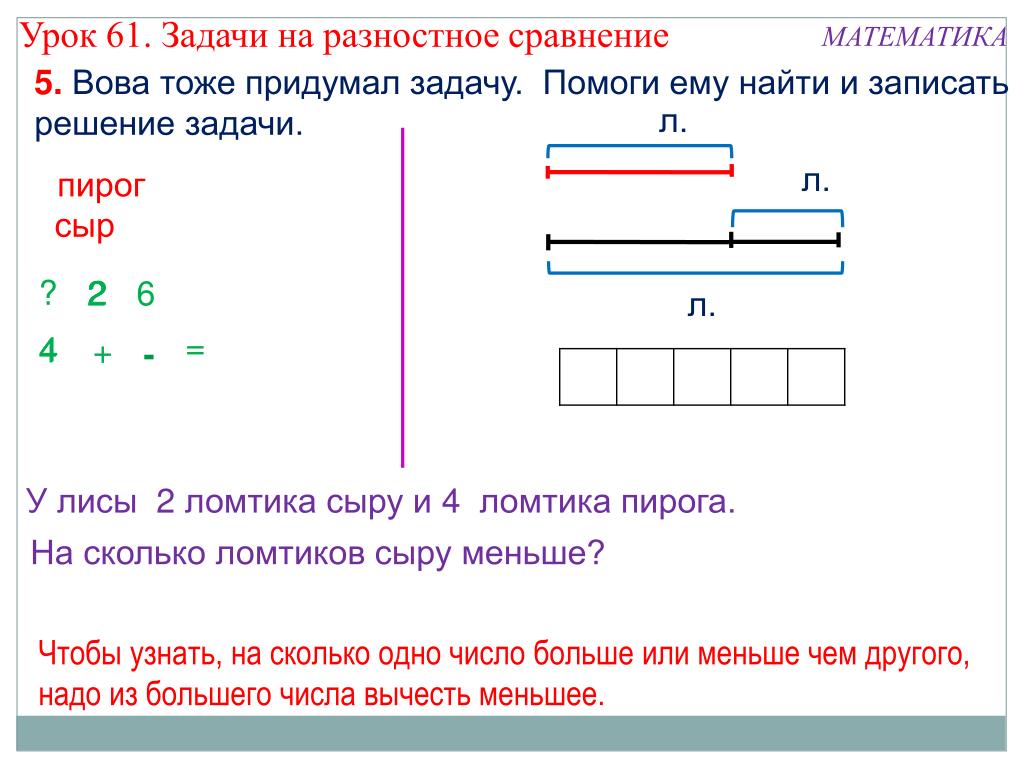 Оно должно отражать всю последовательность действий — так ребёнок сможет запомнить принцип и пользоваться им в дальнейшем. 

4. Формулировка ответа

Ответ должен быть полным и точным. Это не просто формальность: обдумывая ответ, ребёнок привыкает серьёзно относиться к результатам своего труда. А главное — из описания должна быть понятна логика решения.

Задание из базового курса алгебры домашней онлайн-школы «Фоксфорда», 7 класс
‍

Одна из самых распространённых ошибок — представление в ответе не тех данных, о которых спрашивалось изначально. Если такая проблема возникает, нужно вернуться к первому пункту.   

5. Закрепление результата

Не стоит думать, что выполнив задание один раз, ребёнок сразу научится решать задачи. Полученный результат нужно зафиксировать. Для этого подумайте над решённой задачей ещё немного: предложите ребёнку поискать другой способ решения или спросите, как изменится ответ при изменении того или иного параметра в условии.

Важно, чтобы у ребёнка сложился чёткий алгоритм рассуждений и действий в каждом из вариантов.  

В нашей онлайн-школе, помимо уроков, ученики могут закреплять  свои знания на консультациях в формате открытых часов, где учителя разбирают темы, вызвавшие затруднения, показывают необычные задачи и различные способы их решения. 

Что поможет ребёнку решать задачи  

В заключение расскажем о том, как сделать процесс решения задач проще и интереснее:

• Для того чтобы решать задачи, необходимо уметь считать. Следует выучить с ребёнком таблицу умножения, освоить примеры с дробями и простые уравнения.
• Чтобы решение задач не превратилось для ребёнка в рутину, проявите фантазию. Меняйте текст задания в соответствии с интересами ребёнка. Например, решать задачи на движение будет куда интереснее, если заменить банальные поезда трансформерами, летящими навстречу друг другу в эпической схватке. 
• Дети с развитой логикой учатся решать задачи быстрее. Советуем разбавлять чисто математические задания логическими. Задачи «с подвохом» избавят ребёнка от шаблонного мышления, а задания с большим количеством лишних данных научат выделять главное из большого количества условий.    

<<Блок перелинковки>>

После того как ребёнок решит достаточно задач одного типа, предложите ему самому придумать задачу. Это позволит ему не только закрепить материал, но и проявить творческие способности.

Как решать задачи правильно и с чего начать решение задачи

В этой статье Вы узнаете как решать задачи по математике, если не знаете с чего начать.

Часто при решении задач школьники «входят в ступор» — в голове туман, мысли куда-то разбежались, и кажется, что собрать их уже не возможно.

Я хочу на примере решения задачи из Открытого банка заданий показать, какие простые действия нужно сделать, чтобы собраться с мыслями и как решать задачи правильно.

 

 

Как решать задачи. Задание B13 (№ 26582)

Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В. Ответ дайте в км/ч.

1. Внимательно читаем задачу. Возможно, несколько раз.

2. Определяем, о каком процессе идет речь в задаче,  и какие формулы описывают этот процесс. Выписываем эти формулы. В данном случае это задача на движение, и формула, которая описывает этот процесс S=vt.

3. Выписываем размерность каждой переменной, которая входит в состав уравнения:

• S — расстояние  — км
• v — скорость —  км/ч
• t — время — ч

Знание размерности поможет нам при проверке получившихся формул.

4. Выписываем  все  числа, которые встречаются в условии задачи, пишем,  что они обозначают и их размерность:

98 км — расстояние между городами,

7 км/ч  — на столько скорость велосипедиста на обратном пути больше, чем скорость на пути из  города А в город В,

7 часов — время остановки велосипедиста (это время он не ехал)

5. Ещё раз читаем вопрос задачи.

6. Решаем, какую величину мы примем  за неизвестное. Удобно принимать за неизвестное ту величину, которую надо узнать в задаче. В данном случае это скорость велосипедиста на пути из А в В.

Итак: пусть  скорость велосипедиста на пути из А в В равна х. Тогда, поскольку скорость велосипедиста на обратном пути на 7 км/ч больше, чем скорость на пути из  города А в город В, то она равна x+7.

7. Составляем уравнение. Для этого  выразим третью величину уравнения движения (время) через первые две. Тогда:

• время, которое затратил велосипедист на дорогу из А в В равно  98/x,

• а на дорогу из В в А — 98/(x+7)+7 — вспомним, что на пути обратно велосипедист сделал остановку на 7 часов, то есть его время в пути складывается из времени  движение и времени стоянки.

Уравнение составляем для времени. Ещё раз читаем в условии задачи, что в нем говорится о времени: В результате он затратил на обратный путь столько же времени, сколько на путь из А в В. То есть время  «туда » равно времени «обратно». Приравниваем время «туда» и время «обратно» Получим уравнение:

98/x=98/(x+7)+7.

Ещё раза проверяем размерность величин, которые входят в уравнение — нужно следить за тем, чтобы, например, не прибавлять к километрам часы.

8. Решаем уравнение. Теперь нужно сосредоточиться на решении уравнения. Для этого определим, какого типа это уравнение. Поскольку неизвестное находится в знаменателе дробей, это рациональное уравнение. Чтобы его решить, нужно перенести все слагаемые влево и привести дроби к общему знаменателю. Заметим, что числа 98 и 7 кратны 7.

Чтобы упростить решение, разделим обе части уравнения на 7. Получим уравнение: 14/x=14/(x+7)+1

После этого переносим все слагаемые влево, приводим к общему знаменателю, и приравниваем числитель к нулю.

Получаем в числителе: 14(x+7)-14x-x(x+7)=0 Раскроем скобки, приведем подобные слагаемые и решим квадратное уравнение.

Его корни: -14 и 7.

Число -14 не подходит по условию задачи: скорость должна быть положительной.

Ещё раз читаем вопрос задачи и соотносим его с величиной, которую мы нашли: за неизвестное мы приняли скорость велосипедиста на пути из А в В, и эту же величину требуется найти.

Ответ: 7 км/ч.

Как решать задачи. Итог

Заметим, что весь путь решения задачи мы разбили на маленькие кусочки, и на каждом участке сосредотачивались именно на обдумывании конкретного действия. И только после  того, как это действие выполнялось, делали следующий шаг.

Когда не ясно что делать, нужно решить, какой маленький шаг  можно сделать прямо сейчас, сделать его, а потом уже думать о следующем.

Как научить детей решать задачи по математике: советы именитых педагогов и простых мам

Научить детей решать задачи по математике — дело учителя, но и родители не должны оставаться в стороне, если их чадо «тормозит» в этом вопросе. Одним учебником математики сыт не будешь. Ведь если научить ребенка самостоятельно решать задачи в 1-3 классах, дальше он будет щелкать как семечки не только задачи по математике, но и по физике, химии, геометрии и др. И самое главное — этот навык пригодится ребенку в жизни!

vogazeta.ru

В статье Как научить ребенка математике мы подробно писали, из каких 4 частей состоит любая задача и что нужно сделать в первую очередь, чтобы ребенок понял, чего от него хотят и как ответить на вопрос задачи. Уяснив алгоритм решения задач, ребенок сможет самостоятельно решить практически любую задачу, даже несмотря на то, что они все кажутся такими разными. 

Основные типы задач по математике: краткий конспект

Небольшой ликбез, т.к. далеко не все родители учились в педагогических ВУЗах и владеют методикой преподавания. Пробежимся по теории, чтобы понимать, кто, кому и чего «должен». Зная ключевые моменты, вам будет проще помочь ребенку в решении задач, которые вызывают у него сложности, вы сможете определить, где пробелы в знаниях и что нужно «подтянуть» в каждом конкретном случае.

iqsha.ru

Рассмотрим самые распространенные виды задач в начальных классах.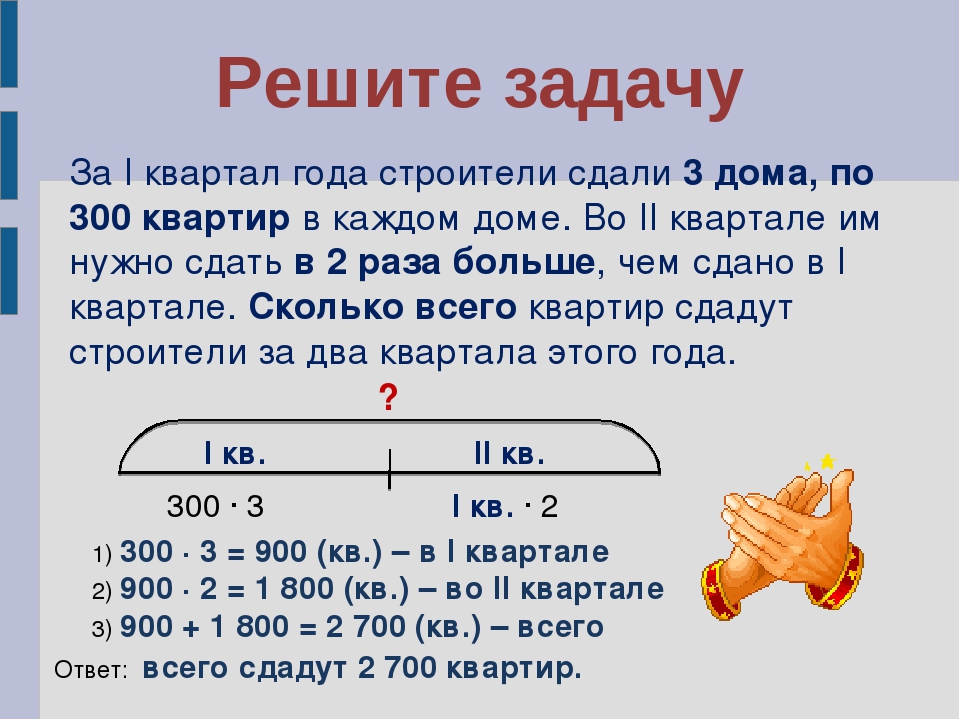

1. Простые задачи на сложение и вычитание

К этой группе относятся несколько задач, но для всех есть общие рекомендации:

• Решаются в одно действие.
• Иногда удобно составить уравнение.
• На их примере ребенок должен научится выполнять краткую запись. 
• Если краткого условия недостаточно, нарисовать рисунок. Если не помог рисунок, показываем на конкретных предметах и производим действия с ними.
• Четко усвоить, что «+» — это прибавить, увеличить, а «-» — уменьшить, отнять, вычесть.
• Хорошо запомнить компоненты арифметических действий:

слагаемое + слагаемое = сумма
уменьшаемое — вычитаемое = разность

• Понять разницу между словами «стало» и «осталось». Четко понимать, что значит «на … меньше», «на … больше».

• Важно понять и запомнить: чтобы узнать, НА СКОЛЬКО одно число больше или меньше другого, нужно из большего числа вычесть меньшее.

• Важно понять и запомнить: чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

 

• Важно понять и запомнить: чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.

 

• Важно понять и запомнить: чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.

Задачи с косвенным вопросом

Это самые коварные задачи из этой группы. Внимательно прочитайте условие — и поймете почему.

На стоянке у первого подъезда 7 машин. Это на 2 машины больше, чем на стоянке у второго подъезда. сколько машин на стоянке у второго подъезда.

2. Составные задачи на сложение и вычитание

Эти задачи решаются двумя и более действиями.

Есть несколько способов решения:

• по действиям с пояснениями;
• по действиям с вопросами;
• выражением.

В решении таких задач главное:

• найти главное и сделать краткую запись;
• разложить эту задачу на несколько простых и составить план решения;
• помнить главное: по двум данным находим третье.

3. Задачи на понимание смысла действий умножения и деления

• Важно запомнить названия компонентов действий и понять их смысл:

1-й множитель х 2-й множитель = произведение
делимое : делитель =частное

• Ребенок должен понимать, что 1-й множитель показывает, КАКОЕ число повторяется а 2-й множитель показывает — СКОЛЬКО РАЗ оно повторяется.

Это очень важно для правильной записи в задачах, иначе получится бессмыслица.

Советы о том, как научить ребенка осознанно относиться к умножению и делению, вы найдете в нашей статье Как научить детей быстро считать: математика до школы. Если возникли проблемы с решением задач на умножение — сдайте чуть-чуть назад, закрепите осознание этого арифметического действия.

4. Простые задачи на умножение и деление

• Очень важно понять и запомнить разницу «в «, «на».

«Во сколько раз» или «на сколько»?  Предлог «на» — это сложение или вычитание, а «в» — умножение или деление.

• Важно понять и запомнить: чтобы узнать, во сколько раз одно число больше или меньше другого, нужно большее число разделить на меньшее.

 5. Составные задачи на все 4 арифметические действия

6. Задачи на цену, количество, стоимость

7. Задачи на движение

Это отдельная обширная тема, вернемся к ней позже.

Типичные ошибки в решении задач

Ошибка №1. Ребенок невнимательно прочитал условие задачи.

Часто бывает так, что ошибки возникают от невнимательности.  Так часто бывает в задачах с косвенным вопросом. Ребенок смотрит на цифры, вроде все логично, но… не верно.

Например: «У Маши 8 конфет, это на 2 меньше, чем у Кати. Сколько конфет у Кати».

Ребенок видит «на 2 меньше» и делает «логичный» вывод, что надо отнять. Отнять можно от бОльшего числа, т.е. сразу напрашивается решение 8-2=6. И ответ: 6 конфет у Кати. А ответ-то не тот! Если внимательно почитать условие, то станет понятно, что у Кати конфет больше чем у Маши. И вовсе тут не отнимать надо.

Как исправить ошибку. Сразу разберитесь с условием, поможет краткая запись.

Ошибка №2. Ребенок допустил ошибку в решении.

Когда в задаче несколько неизвестных, решение затрудняется, требуется выполнить не одно действие, а придумать целую цепочку рассуждений. 

Как исправить ошибку. Для начала определим, каких данных нам не хватает. Решаем по действиям. Находим нужные числа (помним правило: по двум неизвестным находим третье), подставляем их и отвечаем на вопрос задачи.

Ошибка №3. Неправильная запись ответа.

Часто ребенок пишет не то пояснение.

Как исправить ошибку.  Нужно внимательно прочитать вопрос задачи. Уяснить раз и навсегда, что ответ начинается с числа, а дальше пишем, что требовалось найти (переписываем формулировку вопроса задачи). 

Творческий подход в решении задач

www.craftykidsathome.com

• Учите ребенка рассуждать.
• Придумывайте задачи с лишними или недостающими данными.

Пусть ребенок сам вычеркнет лишнее, те данные, которые не влияют на решение.

• Дайте условие, а ребенок пусть сам придумает ответ.
• Пусть ребенок сам составит обратную задачу.
• Придумать несколько задач на одно решение.
• Придумать, как решить задачу другим способом и объяснить его.

На школу надейся, а сам не плошай

Заглянем в педагогику и «расшифруем» мысли умных и заслуженных, исходя из сегодняшних реалий.

В далеком 1867 году К. Ушинский сказал: «У хороших преподавателей дело выходит так, что арифметическая задача есть вместе занимательный рассказ, урок сельского хозяйства или домашней экономии, или историческая или статистическая тема и упражнение в языке».

«Расшифровка» следующая.

• Ученика нужно поставить в такие условия, чтобы он оказался в эпицентре событий, т.е., решая задачу, видел ее применение в жизни.

Не всегда задачи в школьном учебнике «вдохновляют» современных школьников. Многим не ясно условие по одной простой причине: ребенок не имеет представления о том, что говорится. Например, задача про надои и бидоны с молоком, а городской «деть» и корову-то в глаза не видел, не то, что тонны молока в бидонах. Или в задаче использованы такие значения, которые в жизни нереальны — это затрудняет восприятие, т.к. ребенок все воспринимает буквально.

Задача родителей — помочь ребенку ПОНЯТЬ условие. Любым способом: хоть рисуй, хоть танцуй.

• К решению задач нужно подходить творчески.

Интерес заставляет ребенка быть активным, а активность в свою очередь усиливает внимание.

В каждодневной жизни нам то и дело приходится решать задачи. Привлекайте ребенка, задавайте вопросы, просите совета. Например, тема ремонта. Вычислить метраж комнаты; просчитать нужное количество краски, зная расход на метр квадратный; купить линолеум, зная длину и ширину комнаты; просчитать, какой метраж выгоднее, если есть напольное покрытие шириной 2, 5 метра и 3 метра, чтобы меньше остатков было и по цене вышло выгоднее. Купить ткань на пошив постельного белья, зная размеры матраса. Примеров масса! И это работает гораздо эффективнее, чем «бездушная» задача в учебнике, которая совершенно не привязана к жизни и не вызывает эмоциональный отклик.

• При решении жизненных задач у ребенка помимо всего прочего развивается наблюдательность, речь, появляется рабочее настроение, развиваются творческие способности и самостоятельность.

Через некоторое время вы заметите, что ребенок различными способами комбинирует информацию, с легкостью составляет задачи сам, находя идеи в окружающем мире, а не высасывая из пальца.

• Когда ребенка просят составить собственную задачу, нужно следить и за содержанием, и за решением. Задача должна быть осмысленной и целесообразной.

Например, нельзя допускать таких «ляпов», как «Я съел 13 желтых груш и 20 зеленых яблок. Сколько фруктов я съел?» Задача теряет смысл, если она оторвана от жизни.

• От задачи надо идти к примеру, а не наоборот.

Дети мыслят не абстрактно, а конкретными образами. Пример 12-6 ни о чем не говорит, а вот ситуация, когда из 12 человек 6 уже купили билеты на футбольный матч — это совсем другое дело. Тут ребенок не задумываясь ответит, что оставшиеся шестеро очень рискуют, нужно поторопиться, иначе билетов может не хватить и придется сидеть у телевизора, вместо того, чтобы активно скандировать на трибунах в поддержку любимой команды.

Лебединцев в своей книге «Введение в современную методику математики» писал: «То влияние, которое может оказывать обучение счислению и вообще математике на умственное развитие детей, находится в прямой зависимости от материала, которым мы пользуемся при обучении; если в учебном материале будут преобладать отвлеченные упражнения в действиях и хитроумные задачи с условиями, лишенными внутренней связи и, по существу, далекими от жизни, то, упражняя учащихся на таком материале, мы, может быть, и выработаем у них формальные навыки в вычислениях и, пожалуй, изощрим их ум для разгадывания разных ребусов и головоломок, но отнюдь не сделаем их более способными к правильному мышлению в жизни или какой-либо области знания…».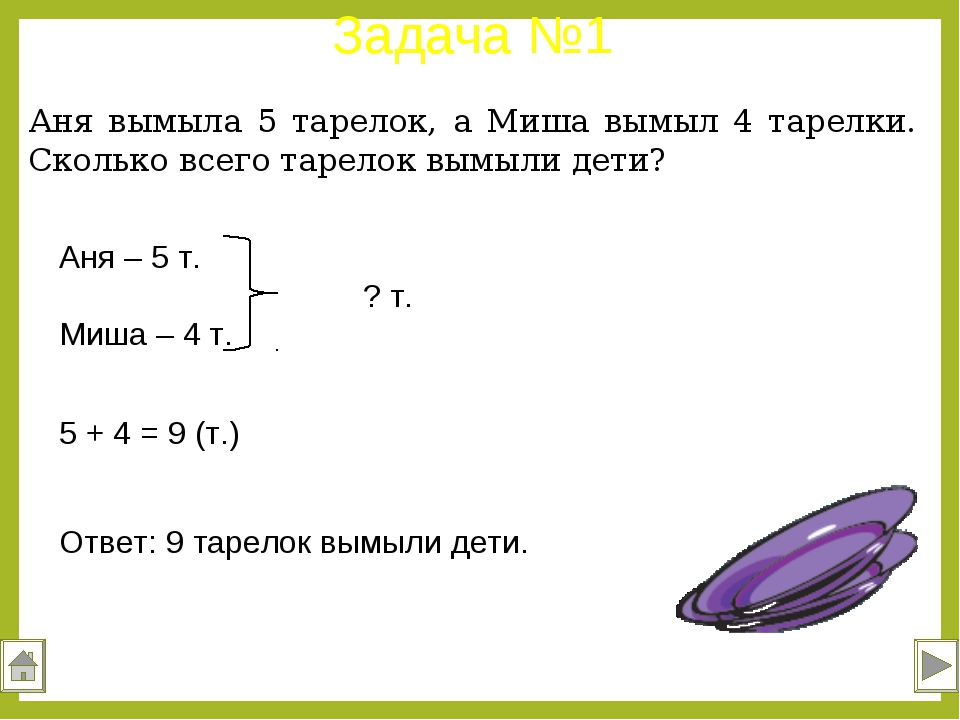

Французский педагог Жан Мосе тоже был уверен, что «заставлять ребенка начинать с отвлеченного правила и затем предлагать ему задачи — это значит идти наперекор ходу развития человеческого ума…».

Практические советы по решению задач от реальных мам

fb.ru

Что нам Ушинский, Лебединцев и Мосе, спросим у тех, кто «из нашей песочницы». Как они помогают своим детям решать задачи по математике, что «работает», какие приемы на практике доказали свою эффективность и помогли повысить успеваемость.

Татьяна, мама учеников 4 кл. и 6 кл. 

«Я знаю, что особую сложность у детей вызывают задачи на скорость, поэтому начала готовить своих мальчишек к этому уже с 1 класса. Когда ехали к бабушке в Пинск, говорили о скорости, засекали время, считали сколько мы проехали км, смотрели на знаки и вычисляли сколько нам останется времени, если мы будем ехать с такой же скоростью и сколько, если папа будет ехать с другой. В общем, я очень удивлялась, когда мои пацаны на скорость задачи решали как орехи.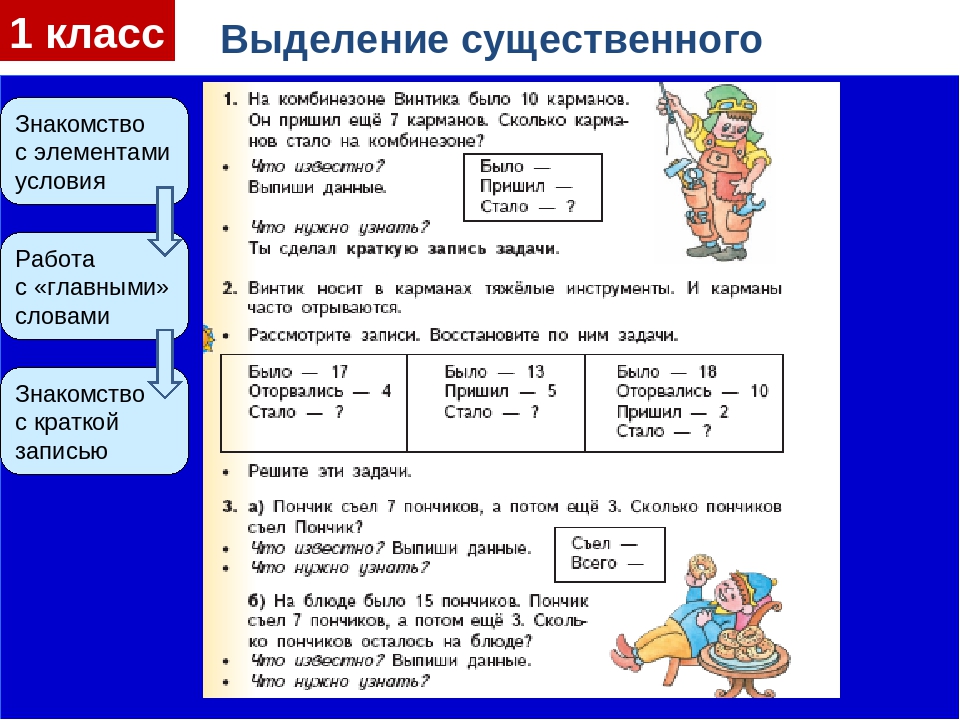 Я поняла, что в моем детстве не хватало практического представления того, о чем говорилось в задачах».

Ольга, мама ученика 1 кл. и ученицы 4 кл.

«С задачами старшая плохо дружит))  Почти всегда приходит за помощью. Стараюсь выработать алгоритм решения, но частенько упираюсь в «лень подумать». Если совсем «затык», рисуем схемы. На дополнительные задачи совсем нет времени, а сама по своей воле заниматься ими дочь точно не будет)) Иногда встречаются задачи с некорректно поставленным вопросом, тут приходится помогать с формулировкой ответа.

Младшего усадить за математику очень сложно. В те редкие моменты, когда дело доходит до задач, он их решает в уме и выдает ответ устно).»

Вероника, мама учеников 2 кл. и 4 кл.

«Младший задачи решает без проблем, но ненавидит чертить схемы к ним и писать пояснения. Старший ходит на факультатив по математике, дома домашку сам делает». 

Катерина, мама ученика 2 кл. и ученицы 5 кл.

«Сын отлично справляется сам. Он такие схемы рисует, что я иногда в шоке)). Если за помощью обращается дочь, стараюсь упростить условие задачи до понятных образов, а потом она сама догадывается, как сложную модель решить».

Татьяна, мама ученицы 5 кл.

«Чаще всего прибегаем к рисованию. Прямо вот как по условию… садимся и рисуем, как есть. Так сказать, наглядность помогает. Велосипедист выехал… значит рисуем человечка на велосипеде, город из которого он выехал и тд)))) Если катер плывет по течению, рисуем море, волны)))))) С пояснениями никогда исправлений со стороны учителя не было, да и у нас, собственно, тоже вопросов не возникало. Смотри по условию, что спрашивают — и пиши ответы возле каждого действия».

Наталья, мама ученика 5 кл.

«Приходилось объяснять дроби на примере сломанных карандашей, порванных в клочья бумажек. В гостях в тот момент был друг-проектировщик, он именно так решил наглядно пояснить сыну задачу. Я обычно прибегаю к помощи рисования. В задачах на скорость/время/расстояние рисовали целые истории: кто куда и на чем поехал, кого встретил по дороге и в какой момент. Порой решение задач превращалось в мультфильм, одного черновика обычно мало. Несколько раз решали задачи всей семьей: мама отдельно от папы, потом сравнивали результаты и каждый объяснял ребенку свой «самый рациональный и простой» способ. Как правило, у мужчин своя логика)), мое решение обычно отличается от папиного».

Уважаемые читатели! Делитесь в комментариях своими находками и сложностями в решении задач по математике с детьми. будем разы разобраться вместе и помочь советами и полезными статьями на интересующие вас темы. 

Решение задачи №19 ЕГЭ по математике. Советы репетитора

Анна Малкова

Задача 19 на профильном ЕГЭ по математике. Раньше ее называли С6. Самая страшная и загадочная. Самая нестандартная. Ни на что не похожая.

Конечно, не совсем… Она похожа на задачи олимпиад по математике. Но в школьных учебниках нет даже намека на эту задачу!

Уравнения в целых числах с несколькими неизвестными. Действия в неопределенной ситуации. Метод «Оценка плюс пример» (а многие о нем даже не слышали). И конечно, культура математических рассуждений. В школе такому не учат! И немногие репетиторы умеют решать задачу 19 профильного ЕГЭ по математике.

Зато она оценивается в целых 4 первичных балла, которые пересчитываются в 9-10 тестовых!

Есть хорошая новость. Можно научиться решать эту загадочную задачу! Более того – это нужно сделать, если вы хотите сдать ЕГЭ по математике на достойные баллы. Или если вы участвуете в олимпиадах по математике.

Многим выпускникам ЕГЭ-Студии эта задача дала необходимые для поступления баллы.

Откроем секрет. Оказывается, что один-два из четырех баллов за задачу 19 профильного ЕГЭ по математике буквально лежат у вас под ногами, и вам надо только нагнуться, чтобы взять их! Как это может быть? Смотрите видео! Учитесь строить оценки и находить нужные примеры.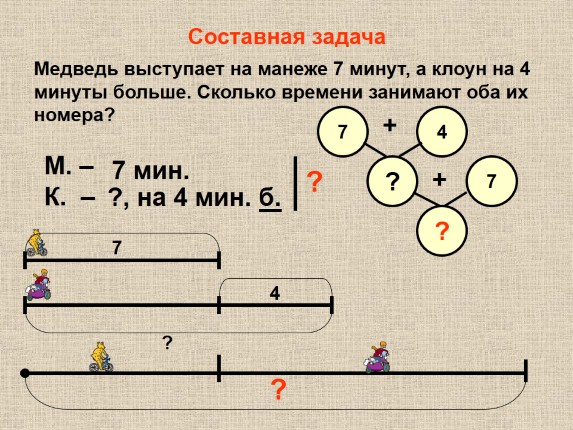 Без этого решить эту странную задачу невозможно. Вы узнаете также, как правильно оформлять решение задачи 19 на профильном ЕГЭ по математике.
Вот задача 19 из варианта ЕГЭ по математике 2017 года. Рассказывает Анна Малкова:

На доске написано 30 различных натуральных чисел, десятичная запись каждого из которых оканчивается или на цифру 2, или на цифру 6. Сумма написанных чисел равна 2454.
а) Может ли на доске быть поровну чисел, оканчивающихся на 2 и на 6.
б) Может ли ровно одно число на доске оканчивается на 6?
в) Какое наименьшее количество чисел, оканчивающихся на 6, может быть записано на доске?

Ну как, сможете решить хотя бы первый пункт задачи 19 на профильном ЕГЭ по математике? Стоит попробовать!

Чтобы научиться решать задачу 19 профильного ЕГЭ по математике, читайте книгу Анны Малковой «Математика. Авторский курс подготовки к ЕГЭ» и смотрите видеокурс «Ключ к С6» из комплекта Премиум.

Удачи на ЕГЭ по математике!

Расскажи друзьям!

Урок 21. задача. структура задачи — Математика — 1 класс

Математика, 1 класс

Урок 21. Задача. Структура задачи.

Перечень вопросов, рассматриваемых на уроке:

1. Решение текстовых задач арифметическим способом.
2. Структура задачи: условие, вопрос, решение, ответ.
3. Решение задач в одно действие на увеличение (уменьшение) числа на несколько единиц.
4. Задачи, содержащие отношения «больше (меньше) на..», «больше (меньше) в…».
5. Дополнение условий задач недостающими данными или вопросом.

Глоссарий по теме

Компоненты задачи – условие, вопрос, решение, ответ.

Задачи на сложение и вычитание.

Взаимосвязь между условием и вопросом задачи.

Элементы задачи:

1. Условие (что известно в задаче).

2. Вопрос (что нужно узнать).

3. Решение (действие, нахождение неизвестного).

4. Ответ задачи (ответ на вопрос задачи).

Ключевые слова

Текстовая задача; условие задачи; вопрос задачи; решение задачи.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. Ч. 1.– М.: Просвещение, 2017.– с. 88 – 89.

2. Моро М. И., Волкова С. И. Математика рабочая тетрадь. 1 кл. 1 ч.– М.: Просвещение, — с. 33 – 34.

На уроке мы узнаем, как построена задача и как называются структурные элементы задачи. Научимся решать задачи, записывать решение задачи и ответ. Сможем выделять задачи из предложенных текстов.

Основное содержание урока

Рассмотрите картинку.

Составьте задачу.

Послушайте два рассказа и сравните их:

1. В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?

2. В магазине мама купила 3 перца и 4 морковки. В овощах очень много витаминов, они очень полезные.

Какой из этих текстов мы будем изучать на уроке математики, а какой на уроке окружающего мира?

Первый текст на уроке математики, так как в нём есть вопрос, для ответа на который нужно выполнить вычисления, а второй на уроке окружающего мира.

Как называется текст с вопросом, для ответа на который нужны математические вычисления?

Такой текст называется «Задача».

Сегодня на уроке мы узнаем, какой текст называется задачей и из каких частей она состоит.

Тема нашего урока: «Задача. Структура задачи».

Посмотрите ещё раз на текст знакомой нам задачи и ответьте на вопрос.

Что в ней известно?

В магазине мама купила 3 перца и 4 морковки. Сколько всего овощей купила мама?

Что мама купила 3 перца и 4 морковки.

Это называется — условие задачи, другими словами, это то, что в задаче известно.

Что в задаче нужно узнать?

Сколько всего овощей купила мама.

Это вопрос задачи. Это о чём спрашивают в задаче, то, что нужно узнать.

Что нужно сделать, чтобы сосчитать, сколько мама купила овощей?

Нужно к трём прибавить четыре, получится семь овощей.

Это решение задачи.

Ещё раз прочитайте вопрос задачи и ответьте на него.

Мама купила семь овощей.

Это ответ задачи.

На уроке мы поймём, как построена задача – в ней есть условие и вопрос.

Будем учиться решать задачи, записывать решение задачи и ответ.

Составьте условие задачи по рисунку.

В корзинке четыре луковицы, ещё две луковицы лежат рядом.

Задайте вопрос.

Сколько всего луковиц?

Как решить такую задачу? Сложением или вычитанием?

Четыре да ещё две, задача решается сложением.

Запишем решение. К четырём прибавить два получится шесть.

Осталось записать ответ задачи. Ответим на вопрос задачи: всего шесть луковиц.

Ещё раз посмотрите внимательно на этот же рисунок:

Составьте другую задачу, которая будет решаться вычитанием:

В корзине было четыре луковицы, из неё взяли две луковицы.

Задайте вопрос.

Сколько луковиц осталось в корзине?

Как записать решение?

Из четырёх вычесть два, получится две луковицы.

Осталось записать ответ задачи.

Разбор тренировочных заданий.

Рассмотрите рисунок, дополните условие и решите задачу.

Ответ:

На огороде с одного куста сорвали 2 кабачка, а с другого куста 6 кабачков. Сколько кабачков собрали с двух кустов?

2 + 6 = 8 (к.)

Ответ: 8 кабачков.

Выберите только те тексты, которые являются математическими задачами.

Ответ:

Верные равенства обозначьте синим цветом, а неверные красным.

Ответ:

Прочитайте задачу и установите соответствия между её компонентами.

Ответ:

Попробуйте заменить овощи соответствующей цифрой.

Подсказка: у каждой цифры своя маска. На одинаковых цифрах — одинаковые маски.

Ответ:

Ответь на вопросы с помощью таблицы.

Ответ:

Покажите разным цветом, как можно получить число 6.

Ответ:

Урок 50. решение задач в 2 действия — Математика — 1 класс

Математика

1 класс

Урок №50

Решение задач в 2 действия

Перечень вопросов, рассматриваемых в теме:

Глоссарий по теме:

Задача – это математический рассказ, в котором есть условие и вопрос. Чтобы ответить на вопрос задачи, ее нужно решить.

Части задачи – условие, вопрос, решение, ответ.

Список литературы:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др.Математика. 1 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ –6-е изд. – М.: Просвещение, 2015. – с.62, 63

2. Волкова С. И. Математика. Проверочные работы. 1 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2014.- с.50, №2, с.51, №2

3. Волкова С. И. Математика. Рабочая тетрадь. 1 кл. 2 часть: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2016.-с.33

Теоретический материал для самостоятельного изучения

Решим задачу.

В одной коробке 6 карандашей, во второй на 2 карандаша меньше. Сколько карандашей в двух коробках?

О чём говорится в задаче? Правильно, о коробках и карандашах.

Что нам известно в задаче? Что в одной коробке было 6 карандашей.

Что сказано о количестве карандашей во второй коробке? Их на 2 меньше, чем в первой коробке.

Что нужно узнать в задаче? Сколько карандашей в двух коробках? Сразу можно ответить на вопрос задачи? Сразу ответить на вопрос задачи нельзя, потому что не сказано, сколько карандашей во второй коробке. Как это можно узнать? От шести отнять два. Теперь можно узнать, сколько всего карандашей в двух коробках? Да.

Составим план решения задачи:

1) Сначала надо узнать, сколько карандашей во второй коробке.

2) Потом можно узнать, сколько всего карандашей в двух коробках.

Решение:

1) 6 – 2 = 4 (к.)

2) 6 + 4 = 10 (к.)

Ответ: всего 10 карандашей.

Рассуждая так же, решим следующую задачу.

На верхней полке 6 книг, а на нижней – на 4 книги больше. Сколько книг на двух полках?

О чём говорится в задаче? О полках и книгах.

Сколько книг на верхней полке? Шесть.

Сколько книг на второй полке? Неизвестно, но сказано, что на 4 книги больше. Т.е. их столько же, сколько на верхней полке, и ещё четыре.

Что нужно узнать в задаче? Сколько книг на двух полках.

Можно ли сразу узнать, сколько книг на двух полках? Нет.

Почему? Мы не знаем, сколько книг на второй полке.

Как найти, сколько книг на второй полке?

Нужно к шести прибавить четыре,получится десять книг.

Теперь можем узнать, сколько книг на двух полках? Да.

Составим план решения задачи:

1) Сначала надо узнать, сколько книг на нижней полке.

2) Потом можно узнать, сколько книг на двух полках.

Решение:

1) 6 + 4 = 10 (кн.)

2) 6 + 10 = 16 (кн.)

Ответ: 16 книг на двух полках.

Тренировочные задания.

1. Выберите задачу, которая решается два действия

Варианты ответов:

1. На одной полке стоят 4 книги, на другой — на 3 книги больше. Сколько книг на второй полке?

2. На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?

3. На первой проволоке 5 шариков, на второй — на 4 шарика больше. Сколько шариков на второй проволоке?

Правильный ответ:

2.На одной клумбе распустилось 6 тюльпанов, а на другой — на 3 тюльпана меньше. Сколько тюльпанов распустилось на двух клумбах?

2. Решите задачу и выделите цветом правильное решение.

В одной вазе лежало 6 яблок, в другой на 3 яблока меньше. Сколько яблок в двух вазах?

Варианты ответов:

Первый вариант: 6 – 3 = 3 (яб.)

Второй вариант: 6 + 3 = 9 (яб.)

Третий вариант:

1) 6-3=3 (яб.)

2) 6+3=9 (яб.)

Вспомним, что эта задача решается в 2 действия, следовательно, верным будет третий вариант.

Правильный ответ:

1) 6-3=3 (яб.)

2) 6+3=9 (яб.)

9 простых задач на математику

Ссыл­ку на эту ста­тью може­те исполь­зо­вать, что­бы про­ве­рить базо­вые мате­ма­ти­че­ские навы­ки любо­го чело­ве­ка. Кида­е­те ему ссыл­ку и про­си­те при вас (не читая реше­ния) поре­шать какие угод­но задач­ки. Все эти задач­ки уже у нас были в раз­ное вре­мя в этом году. Поэто­му если вы наш хард­кор­ный чита­тель с само­го мар­та, то може­те спо­кой­но меди­ти­ро­вать сле­ду­ю­щие пять минут, это кайф.

Таракан на стене

В ваш подъ­езд дву­мя эта­жа­ми ниже въе­ха­ли новые жиль­цы, кото­рые при­вез­ли с собой тара­ка­нов, но не при­вез­ли еды. Насе­ко­мые в поис­ках еды ста­ли полз­ти вверх по вен­ти­ля­ци­он­ной шах­те и ско­ро добе­рут­ся до вашей квар­ти­ры. Но караб­кать­ся вверх им неудоб­но: за час они под­ни­ма­ют­ся на 1 м, но сра­зу после это­го теря­ют рав­но­ве­сие и ска­ты­ва­ют­ся на ⅔ м вниз.

Вопрос: сколь­ко часов у вас есть на покуп­ку лову­шек для тара­ка­нов, если рас­сто­я­ние от вас до сосе­дей по вен­ти­ля­ци­он­ной шах­те — 7 м?

За один пол­ный час тара­кан про­пол­за­ет ⅓ м: под­ни­ма­ет­ся на метр и опус­ка­ет­ся на ⅔:

1 — ⅔ = ⅓ м — про­пол­за­ет тара­кан за час.

С дру­гой сто­ро­ны, послед­ний метр тара­кан про­пол­зёт тоже за 1 час: он добе­рёт­ся до вер­ха за 60 минут, но ска­ты­вать­ся вниз ему уже не надо, пото­му что он достиг ров­ной поверх­но­сти. Зна­чит, нуж­но узнать, сколь­ко вре­ме­ни ему пона­до­бит­ся на остав­ши­е­ся 6 м:

7 м до вас — 1 м, кото­рый он про­пол­зёт за один заход = 6 м, кото­рые тара­кан будет мед­лен­но полз­ти и скатываться.

Что­бы узнать остав­ше­е­ся вре­мя, раз­де­лим рас­сто­я­ние на скорость:

6 м / ⅓ м в час = 18 часов.

Полу­ча­ет­ся, что тара­кан про­пол­зёт 6 м за 18 часов, а остав­ший­ся метр пре­одо­ле­ет за час, пото­му что ска­ты­вать­ся уже не при­дёт­ся. Полу­ча­ем общее время:

18 + 1 = 19 часов.

Зна­чит, у вас есть 19 часов на то, что­бы купить ловуш­ки и гель от тара­ка­нов. Логика!

Долгий перелёт

Пред­ставь­те, что вам нуж­но пару раз по рабо­те сле­тать из Моск­вы во Вла­ди­во­сток и вер­нуть­ся назад. Пер­вый раз вы лети­те туда и обрат­но при пол­ном шти­ле. Во вто­рой раз при точ­но таком же пере­лё­те в оба кон­ца посто­ян­но дует запад­ный ветер оди­на­ко­вой силы: туда попут­ный, а обрат­но — лобо­вой. Как изме­нит­ся общее вре­мя полё­та во вто­ром слу­чае: умень­шит­ся, уве­ли­чит­ся или оста­нет­ся таким же, как в пер­вом случае?

Самая пер­вая реак­ция на такую зада­чу — ска­зать, что вре­мя не изме­нит­ся. Всё кажет­ся логич­ным: когда летишь туда, ветер чуть уско­ря­ет само­лёт, а когда обрат­но — точ­но так же замед­ля­ет. Но это вер­но толь­ко наполовину.

В рам­ках зада­чи при­мем ско­рость само­лё­та за 800 кило­мет­ров в час. А ветер пусть дует со ско­ро­стью 100 кило­мет­ров в час. Мы зна­ем, что в реаль­ных усло­ви­ях всё намно­го слож­нее и ско­ро­сти нель­зя скла­ды­вать напря­мую, но для упро­ще­ния допу­стим, что это воз­мож­но. Рас­сто­я­ние от Моск­вы до Вла­ди­во­сто­ка по воз­ду­ху — 6 400 километров.

Первая командировка — без ветра

Если вет­ра нет, то у нас есть толь­ко ско­рость само­лё­та, кото­рая не меня­ет­ся в обо­их слу­ча­ях. Рас­сто­я­ние тоже оди­на­ко­вое, зна­чит вре­мя полё­та будет неиз­мен­ным в путе­ше­ствии туда и обрат­но. Най­дём его:

6 400 / 800 = 8 часов.

Это зна­чит, что в без­вет­рен­ную пого­ду наш само­лёт будет лететь из Моск­вы во Вла­ди­во­сток 8 часов, и столь­ко же лететь обрат­но. В сум­ме — 16 часов.

Вторая командировка — дует постоянный ветер

Когда летишь во Вла­ди­во­сток и дует попут­ный ветер, само­лёт и в самом деле летит быст­рее: ско­рость послед­не­го скла­ды­ва­ет­ся со ско­ро­стью ветра.

800 + 100 = 900 (км/ч).

Тогда само­лёт наше рас­сто­я­ние прой­дёт за 7 часов 7 минут:

6 400 / 900 = 7,11 часа.

Когда летишь обрат­но и дует встреч­ный ветер, то ско­рость само­лё­та падает:

800 — 100 = 700 (км/ч).

И путь обрат­но он с этой ско­ро­стью про­де­ла­ет уже за 9 часов 8 минут:

6 400 / 700 = 9,14 часа.

Полу­ча­ет­ся, что общее вре­мя туда и обрат­но при таком вет­ре будет равно:

7 часов 7 минут + 9 часов 8 минут = 16 часов 15 минут.

Посто­ян­ный ветер уве­ли­чи­ва­ет общее вре­мя полё­та, и чем силь­нее ветер — тем боль­ше вре­ме­ни зай­мёт полёт.

Если ветер будет дуть в 3 раза силь­нее — 300 кило­мет­ров в час, то до Вла­ди­во­сто­ка само­лёт доле­тит за 5 часов 48 минут, а обрат­но ему потре­бу­ет­ся уже 12 часов 48 минут, что в сум­ме даст 18 часов 36 минут.

Но почему?

Пото­му что математика:

6 400 / 800 + 6 400 / 800 = 16.

6 400 / 900 + 6 400 / 700 = 16,25.

Полторы белки

Пол­то­ры бел­ки за пол­то­ры мину­ты съе­да­ют пол­то­ра оре­ха. Сколь­ко оре­хов съе­дят 9 белок за 9 минут?

Пер­вое, что хочет­ся сра­зу отве­тить — 9 оре­хов. Но это было бы слиш­ком просто.

Самое безум­ное в этой зада­че — пол­то­ры бел­ки. Давай­те от них изба­вим­ся и будем даль­ше рабо­тать уже с целы­ми животными.

Даль­ше в реше­нии будем исхо­дить из того, что бел­ки всё едят одно­вре­мен­но друг с дру­гом, неза­ви­си­мо от их коли­че­ства. В обыч­ной жиз­ни так и про­ис­хо­дит, и мы тоже будем при­дер­жи­вать­ся того же.

Узна­ем, на что спо­соб­на одна бел­ка за пол­то­ры минуты:

1,5 бел­ки за 1,5 мину­ты съе­да­ют 1,5 оре­ха → 1 бел­ка за те же 1,5 мину­ты съест 1 орех.

Теперь выяс­ним, сколь­ко оре­хов она съест за 9 минут. Для это­го нам нуж­но пол­то­ры мину­ты умно­жить на 6, а зна­чит и коли­че­ство съе­ден­но­го тоже нуж­но умно­жить на 6:

1 бел­ка за (1,5 * 6) минут съест (1 * 6) орехов

↓

1 бел­ка за 9 минут съест 6 орехов. 

Оста­лось запу­стить 9 белок одно­вре­мен­но и посчи­тать, сколь­ко оре­хов они оси­лят за те же 9 минут:

(1 * 9) белок за 9 минут съе­дят (6 * 9) орехов

↓

9 белок за 9 минут съе­дят 54 ореха!

Поче­му? Пото­му что математика!

Рекрутер и бесконечный офис

В одной круп­ной ком­па­нии появил­ся безум­ный рекру­тер, кото­рый нани­мал на рабо­ту толь­ко джу­ни­о­ров. У него был хит­рый план — запол­нить ими весь офис и полу­чить за это пре­мию от началь­ства. Что­бы это сде­лать, он каж­дый день нани­мал столь­ко же людей, сколь­ко уже рабо­та­ет в офи­се. Гру­бо гово­ря, удва­и­вал чис­ло джуниоров.

Когда он толь­ко начи­нал, в ста­ром офи­се рабо­тал толь­ко один джу­ни­ор, но 30 дней спу­стя все рабо­чие места в офи­се были пол­но­стью заня­ты напу­ган­ны­ми, ниче­го не пони­ма­ю­щи­ми джуниорами.

В новом, точ­но таком же по раз­ме­ру офи­се с пер­во­го дня рабо­та­ет в 2 раза боль­ше людей, чем на стар­те в ста­ром — целых 2 джу­ни­о­ра вме­сто одно­го. Сколь­ко вре­ме­ни уйдёт у безум­но­го рекру­те­ра на то, что­бы запол­нить новый офис и полу­чить свою квар­таль­ную премию?

Каза­лось бы, что если на стар­те в 2 раза боль­ше людей, то и новый офис запол­нит­ся быст­рее в 2 раза — за 15 дней вме­сто 30, но это не так.

Смысл в том, что, по усло­вию зада­чи, рекру­тер удва­и­ва­ет чис­ло людей каж­дый день. Это зна­чит, что в новом офи­се это удво­е­ние про­изо­шло фак­ти­че­ски на день рань­ше, чем в ста­ром, а зна­чит, и джу­ни­о­ры его пол­но­стью зай­мут толь­ко на день рань­ше — за 29 дней вме­сто 30.

Если вы люби­те точ­ные мате­ма­ти­че­ские реше­ния вме­сто рас­суж­де­ний — вот реше­ние. Сна­ча­ла посчи­та­ем, сколь­ко людей все­го вме­ща­ет каж­дый офис. Для это­го запи­шем каж­дые удво­е­ния начи­ная с одно­го джуниора:

день 1: 1 джуниор

день 2: 2 джуниора

день 3: 4 джуниора

день 4: 8 джуниоров . . .

Если выве­сти общую фор­му­лу, получим:

день 1: 2 в нуле­вой сте­пе­ни джуниоров

день 2: 2¹ джуниоров

день 3: 2² джуниоров

день 4: 2³ джуниоров

. . .

день 30: 2 в 29-й сте­пе­ни джуниоров

Полу­ча­ет­ся, что наш офис вме­ща­ет 2 в 29-й сте­пе­ни джу­ни­о­ров. Если удво­е­ние про­ис­хо­дит каж­дый день и на стар­те у нас 2 джу­ни­о­ра, то для ново­го офи­са полу­чим такое урав­не­ние, где х — коли­че­ство дней:

2 в 29-й сте­пе­ни = 2 в сте­пе­ни х

Оче­вид­но, что х = 29, а, зна­чит, на запол­не­ние все­го ново­го офи­са пона­до­бит­ся 29 дней, как мы и гово­ри­ли в начале.

Задача про бармена и гурмана

У бар­ме­на экс­клю­зив­но­го лофт-хипста-бара на ули­це Рубин­штей­на есть толь­ко два оди­на­ко­вых ста­ка­на по 150 мл. Один ста­кан — пол­ный, и в нём про­стая вода, а в дру­гом 40-градусная вод­ка, и он напо­ло­ви­ну пуст. Утро-с.

В бар зашёл посе­ти­тель и попро­сил сде­лать ему 15-градусный рас­твор спир­та. Наход­чи­вый бар­мен не рас­те­рял­ся и смог при­го­то­вить его, исполь­зуя толь­ко эти два ста­ка­на. Как он это сде­лал и какой объ­ём полу­чил­ся в итоге?

Вряд ли эта зада­ча когда-нибудь попа­дёт­ся на собе­се­до­ва­нии в ИТ-компанию, но она может при­го­дить­ся в реаль­ной жиз­ни — напри­мер, завтра.

Это вари­ант клас­си­че­ской зада­чи на пере­ли­ва­ния, толь­ко надо счи­тать ещё кре­пость рас­тво­ра и его объём.

Берём полу­пу­стой ста­кан с вод­кой и доли­ва­ем в него воды до пол­но­го. Полу­ча­ем целый ста­кан 20-градусного спир­та ((40 + 0) / 2 = 20). Во вто­ром ста­кане оста­лась поло­ви­на чистой воды, она нам сей­час пригодится.

В ста­кан с остав­шей­ся водой нали­ва­ем наш рас­твор спир­та — сно­ва до кра­ёв. В нём теперь 10 гра­ду­сов ((20 + 0) / 2 = 10). В дру­гом оста­лось пол­ста­ка­на 20-градусного спирта.

Финаль­ным эта­пом бар­мен берёт и раз­бав­ля­ет эти пол­ста­ка­на 10-градусным рас­тво­ром из пол­но­го ста­ка­на так, что­бы жид­кость сно­ва дошла до края. В ито­ге полу­ча­ет­ся 15-градусный рас­твор ((20 + 10) / 2 = 15) объ­ё­мом в 150 мл!

Популярная школьная задача

Вот вам очень про­стой мате­ма­ти­че­ский пример:

8 / 2(2 + 2)

Вы уди­ви­тесь, но боль­шин­ство людей не смо­гут пра­виль­но это посчи­тать. Посчи­тай­те сами и потом смот­ри­те пра­виль­ный ответ:

В интер­не­те мно­го спо­ров про такие при­ме­ры, поэто­му мы реши­ли разо­брать­ся, какие ошиб­ки совер­ша­ют чаще все­го и поче­му мно­гие счи­та­ют непра­виль­но. Для реше­ния нам пона­до­бят­ся три мате­ма­ти­че­ских правила:

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. Если ско­бок несколь­ко, они выпол­ня­ют­ся сле­ва направо.
2. При отсут­ствии ско­бок мате­ма­ти­че­ские дей­ствия выпол­ня­ют­ся сле­ва напра­во, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычитание.
3. Меж­ду мно­жи­те­лем и скоб­кой (или дву­мя скоб­ка­ми) может опус­кать­ся знак умножения.

Раз­бе­рём подроб­нее, что это зна­чит в нашем случае.

1. То, что в скоб­ках, выпол­ня­ет­ся в первую оче­редь. То есть в нашем при­ме­ре, вне зави­си­мо­сти от чего угод­но, сна­ча­ла схлоп­нут­ся скобки:

8 / 2(2 + 2) → 8 / 2(4)

2. Меж­ду чис­лом и скоб­кой мож­но опу­стить знак умно­же­ния. У нас перед скоб­кой двой­ка, то есть мож­но сде­лать такую замену:

8 / 2(4) → 8 / 2 × 4

3. Мате­ма­ти­че­ские дей­ствия при отсут­ствии ско­бок выпол­ня­ют­ся сле­ва напра­во: как при чте­нии, сна­ча­ла умно­же­ние и деле­ние, потом — сло­же­ние и вычи­та­ние. Умно­же­ние и деле­ние име­ют оди­на­ко­вый при­о­ри­тет. Нет тако­го, что сна­ча­ла все­гда дела­ет­ся умно­же­ние, затем деле­ние, или наобо­рот. Со сло­же­ни­ем и вычи­та­ни­ем то же самое.

Неко­то­рые счи­та­ют, что раз мно­жи­те­ли были напи­са­ны близ­ко друг к дру­гу (когда там сто­я­ли скоб­ки), то оно выпол­ня­ет­ся в первую оче­редь, ссы­ла­ясь при этом на раз­ные мето­ди­че­ские посо­бия. На самом деле это не так, и нет тако­го скры­то­го умно­же­ния, кото­рое име­ет при­о­ри­тет над дру­гим умно­же­ни­ем или деле­ни­ем. Это такое же умно­же­ние, как и осталь­ные, и оно дела­ет­ся в общем поряд­ке — как и при­ня­то во всём мате­ма­ти­че­ском мире.

Полу­ча­ет­ся, что нам сна­ча­ла надо сло­жить 2 + 2 в скоб­ках, потом 8 раз­де­лить на 2, и полу­чен­ный резуль­тат умно­жить на то, что в скобках:

8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16

Кста­ти, если на айфоне запи­сать это выра­же­ние точ­но так же, как в усло­вии, теле­фон тоже даст пра­виль­ный ответ.

А инже­нер­ный каль­ку­ля­тор на Windows 10 так запи­сы­вать не уме­ет и про­пус­ка­ет первую двойку-множитель. Попро­буй­те сами 🙂

Тут в тред вры­ва­ют­ся мате­ма­ти­ки и с воп­ля­ми «Шустеф!» пояс­ня­ют криком:

«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исклю­че­ние: в алгеб­ре знак умно­же­ния свя­зы­ва­ет ком­по­нен­ты дей­ствия силь­нее, чем знак деле­ния, поэто­му знак умно­же­ния опус­ка­ет­ся. Напри­мер, a:b·c= a: (b·c)».

Этот текст из «Мето­ди­ки пре­по­да­ва­ния алгеб­ры», курс лек­ций, Шустеф М. Ф., 1967 год. (стр. 43)

Раз в спор­ном при­ме­ре знак умно­же­ния опу­щен, то спор­ный при­мер алгеб­ра­и­че­ский, а зна­чит, сна­ча­ла умно­жа­ем 2 на 4, а потом 8 делим на 8!

Та самая цитата. 

А вот как на это отве­ча­ют те, кто дей­стви­тель­но в теме и не ленит­ся пол­но­стью посмот­реть первоисточник:

«Для устра­не­ния недо­ра­зу­ме­ний В. Л. Гон­ча­ров ука­зы­ва­ет, что пред­по­чти­тель­нее поль­зо­вать­ся в каче­стве зна­ка деле­ния чер­той и ста­вить скоб­ки [87]. П. С. Алек­сан­дров и А. Н. Кол­мо­го­ров [59] пред­ло­жи­ли изме­нить поря­док дей­ствий в ариф­ме­ти­ке и решать, напри­мер, так: 80:20×2=80:40=2 вме­сто обыч­но­го: 80:20×2=4×2=8. Одна­ко это пред­ло­же­ние не нашло поддержки».

Если апел­ли­ро­вать к Фри­де Мак­совне Шустеф, то выхо­дит, что:

1. В. Л. Гон­ча­ров гово­рит так: «Ребя­та, исполь­зуй­те чер­ту и ставь­те скоб­ки, что­бы ни у кого не было вопро­сов про приоритет».
2. Если у нас всё же бит­ва ариф­ме­ти­ки и алгеб­ры, то, по П. С. Алек­сан­дро­ву и А. Н. Кол­мо­го­ро­ву, при­мер нуж­но решать сле­ва напра­во, как обыч­но. Они, конеч­но, пред­ло­жи­ли решать такое по-другому, но науч­ное сооб­ще­ство их не поддержало.

Самое инте­рес­ное, что даль­ше в при­ме­рах Фри­да Мак­сов­на поль­зу­ет­ся как раз пра­виль­ным поряд­ком дей­ствий, объ­яс­няя реше­ние. Даже там, где есть умно­же­ние на скоб­ку с опу­щен­ным зна­ком, она выпол­ня­ет дей­ствия сле­ва направо.

Пол­ная цита­та из Шустеф, кото­рая, ока­зы­ва­ет­ся, име­ет в виду совсем не то. 

Что не так с отчётом?

Один тре­бо­ва­тель­ный HR-директор дал зада­ние мене­дже­ру: про­ве­сти опрос сре­ди веб-программистов и выяс­нить, на каком язы­ке они пишут чаще все­го — на JavaScript или на PHP. Через неде­лю мене­джер при­нёс такой отчёт:

• коли­че­ство опро­шен­ных — 300;
• уме­ет писать на JavaScript — 234;
• уме­ет писать на PHP — 213;
• уме­ют писать на обо­их язы­ках — 144;
• вооб­ще не пишут код — 0.

HR-директор посмот­рел на отчёт и ска­зал мене­дже­ру «У тебя ошиб­ка в отчё­те. Дан­ные фаль­си­фи­ци­ро­ва­ны. Ты уво­лен в свя­зи с утра­той дове­рия». За какую ошиб­ку уво­ли­ли менеджера?

Что­бы най­ти ошиб­ку, давай­те про­ве­рим циф­ры из отчё­та и срав­ним их с исход­ны­ми. Для нача­ла выяс­ним, кто уме­ет писать ТОЛЬКО на JavaScript. Что­бы это сде­лать, возь­мём тех, кто уме­ет на нём писать, и вычтем отту­да тех, кто пишет на обо­их языках:

234 − 144 = 90 (чистых JavaScript-программистов)

Точ­но так же посчи­та­ем тех, кто пишет ТОЛЬКО на PHP: возь­мём общее коли­че­ство PHP-программистов и вычтем из них тех, кто уме­ет писать на обо­их языках.

213 − 144 = 69 (чистых PHP-программистов)

А теперь сло­жим три груп­пы: тех, кто пишет толь­ко на JavaScript (90 чело­век), кто пишет толь­ко на PHP (69 чело­век) и тех, кто пишет на двух язы­ках сра­зу (144 человека).

90 + 69 + 144 = 303

Полу­чи­лось 303 чело­ве­ка, а в опро­се заяв­ле­но 300.

Понят­но, что рас­хож­де­ние в 3 чело­ве­ка не вли­я­ет на общую ста­ти­сти­ку, но для тре­бо­ва­тель­но­го HR-директора это­го было достаточно.

Программисты и часы

— Доб­рое утро. Кото­рый сей­час час?

— Сло­жи 1/4 вре­ме­ни, про­шед­ше­го с полу­но­чи до сей­час, с 1/2 от сей­час до полуночи.

— Спа­си­бо, я понял.

— Не сомневался.

Вопрос: кото­рый час?

На самом деле это очень про­стая зада­ча, если пом­нить, что в сут­ках 24 часа.

Пусть от полу­но­чи до сей­час про­шло Х вре­ме­ни. Тогда от сей­час до полу­но­чи оста­лось 24 – Х времени.

С дру­гой сто­ро­ны, если мы сло­жим чет­верть вре­ме­ни от полу­но­чи до сей­час и поло­ви­ну вре­ме­ни от сей­час до полу­но­чи, то как раз полу­чим Х — вре­мя, кото­рое сейчас:

(¼ × Х) + (½ × (24 − Х)) = Х

Рас­кры­ва­ем скобки:

Х/4 + 12 − Х/2 = Х

Пере­не­сём все Х в одну сто­ро­ну, а 12 — в другую:

Х − Х/4 + Х/2 = 12

Х + Х/4 = 12

5Х/4 = 12

5Х = 48

Х = 9,6

Полу­ча­ет­ся, что с полу­но­чи про­шло 9,6 часа, или 9 часов 36 минут.

Ответ: на часах 9:36.

Необычный автосалон

Один авто­са­лон купил подер­жан­ную маши­ну за 450 тысяч и через неде­лю про­дал её за 525 тысяч. Дирек­тор сало­на решил, что такая модель поль­зу­ет­ся спро­сом, так что он дал мене­дже­рам зада­ние — най­ти ещё одну подоб­ную маши­ну. Они нашли такую же за 550 тысяч, купи­ли её, но дирек­тор повёл себя стран­но. Он сно­ва поста­вил на неё цен­ник в 525 тысяч, и маши­на ушла за два дня. Помо­ги­те бух­гал­те­рии понять, зара­бо­тал в ито­ге салон или поте­рял часть денег?

У этой зада­чи три реше­ния: инту­и­тив­ное, поша­го­вое и бух­гал­тер­ское. Срав­ни­те подходы.

Мно­гие реша­ют эту зада­чу так:

1. Было 450 тысяч.
2. Купи­ли маши­ну и про­да­ли за 525 тысяч.
3. После про­да­жи зара­бо­та­ли 75.
4. Взя­ли в долг 25.
5. Купи­ли вто­рую маши­ну и про­да­ли сно­ва за 525.
6. Изна­чаль­но было 450, ста­ло 525, зна­чит, при­быль сно­ва соста­ви­ла 75 тысяч, а общая — 150 тысяч.
7. Отда­ём 25 дол­га, полу­ча­ем при­быль 125 тысяч.

Но это непра­виль­но. Пра­виль­но — ниже.

Давай­те раз­бе­рём эту сдел­ку по шагам, что­бы понять, сколь­ко денег было у сало­на на каж­дом этапе.

В самом нача­ле у них было 450 тысяч — запом­ним это. Эти день­ги пошли на покуп­ку пер­вой маши­ны, поэто­му на вто­ром шаге у сало­на ста­ло 0 руб­лей, но появил­ся автомобиль.

На тре­тьем шаге его про­да­ли за 525 тысяч, кото­рые и ушли в кас­су. Пока при­быль сало­на рав­на: 525 − 450 = 75 тысяч.

Вто­рая маши­на сто­и­ла на 25 тысяч доро­же, чем у них было — 550, поэто­му салон взял в долг 25 тысяч и купил её (шаг номер четы­ре). Здесь при­быль сало­на исчез­ла и появил­ся убы­ток в 25 тысяч.

Пятым шагом они про­да­ли вто­рую маши­ну за 525 тысяч, поло­жи­ли день­ги в кас­су и ста­ли раз­би­рать­ся с дол­га­ми. После того как они вер­ну­ли сум­му, кото­рую были долж­ны, у сало­на оста­лось 500 тысяч, а начи­на­ли они с сум­мы в 450 тысяч. Полу­ча­ет­ся, что они зара­бо­та­ли 500 − 450 = 50 тысяч.

Бух­гал­те­ры рабо­та­ют так: счи­та­ют все дохо­ды и рас­хо­ды, а потом нахо­дят саль­до — раз­ни­цу меж­ду ними. Сде­ла­ем то же самое.

Дохо­ды: 525 с пер­вой про­да­жи и столь­ко же со вто­рой. Полу­ча­ет­ся 525 + 525 = 1050 тысяч.

Рас­хо­ды: 450 за первую маши­ну и 550 за вто­рую. Полу­ча­ет­ся 450 + 550 = 1000 тысяч.

Саль­до: дохо­ды минус рас­хо­ды. Это 1050 − 1000 = 50 тысяч.

4 шага для решения даже самой сложной математической задачи

Есть несколько способов решить математические задачи; однако упрощенный метод, который может помочь каждому решить даже самую сложную проблему, представляет собой трехэтапный процесс.

Процесс:

1. Визуализируйте проблему
2. Подход, которого нужно придерживаться для этой проблемы
3. Наконец, решите задачу

Этот трехэтапный процесс, вероятно, поможет вам улучшить ваши общие математические навыки .

Вот четыре шага, которые помогут легко решить любые математические задачи:

1.Внимательно прочтите, поймите и определите тип задачи

Определите категорию, к которой относится ваша математическая задача, прежде чем двигаться дальше, поскольку это поможет найти лучшее решение для ее решения.

Когда вы впервые начинаете изучать математику, проверьте тип задачи — проблема со словами, о дробях, квадратные уравнения или любой другой тип.

Определите категорию, к которой относится ваша математическая задача, прежде чем двигаться дальше, поскольку это поможет найти лучшее решение для ее решения.

Внимательное прочтение проблемы и обеспечение правильного понимания проблемы чрезвычайно важно для выполнения следующих шагов.

2. Нарисуйте и проанализируйте свою задачу

Возможно, вы также можете поискать шаблоны или использовать графики для решения математической задачи.

После того, как вы поняли проблему, следующим шагом может быть ее описание, поскольку это поможет вам в дальнейшем. Рисунок может быть простым в виде фигур или фигур с числами.

Здесь вы также, вероятно, могли бы поискать закономерности или использовать графики. После того, как весь этот процесс понимания, чтения и рисования будет завершен, вам необходимо пересмотреть анализ, который вы сделали на его основе.

Это поможет вам определиться с типом проблемы и методом ее решения.

3. Разработайте план решения

Во-первых, нужно выяснить формулу, которая понадобится вам для решения математической задачи.

Есть четыре простых шага, которые нужно пройти, чтобы разработать план решения этой проблемы.Шаги, указанные ниже:

• Во-первых, нужно выяснить формулу, которая понадобится вам для решения проблемы. Здесь вам нужно потратить некоторое время на изучение концепций в ваших учебниках, которые помогут вам решить проблему.

• Вам нужно записать свои потребности, чтобы получить ответ на вашу проблему. Для этого вам нужно составить пошаговый список того, что вам нужно для решения проблемы, а также помочь вам оставаться организованным

• Если есть более простая проблема, которая доступна, вы, вероятно, могли бы работать на то, чтобы сначала ее решить.Иногда формулы повторяются для решения обеих проблем. Это даст вам больше времени для решения сложной проблемы.

• Вы можете сделать обоснованное предположение об ответе, чтобы вы могли попытаться получить приблизительный ответ, прежде чем приступить к его решению. Здесь вы можете определить количество и другие факторы, которые будут способствовать тому же. Наконец, просмотрите оценку, а затем проверьте, не упустили ли вы что-нибудь

4. Решите проблему

Убедитесь, что все шаги, которые вы перечислили для решения математической задачи, выполнены.

Как только ваша стратегия и метод решения проблемы готовы, вы можете приступить к ее решению.Шаги следующие:

• Убедитесь, что все шаги, которые вы указали для решения проблемы, выполнены. Перекрестно проверьте каждый из ваших ответов, чтобы убедиться, что точность идеальна.

• Сравните ответ с оценками, которые вы указали после завершения каждого шага. Это поможет вам сэкономить время, если конечный результат окажется не тем, что вы искали. Также проверьте, тщательно ли вы выполнили все шаги.

• Если в середине вы понимаете, что ваш план не работает, вы всегда можете вернуться к этапу планирования и составить новый план.Иногда это происходит из-за типичных ошибок, но вам следует научиться принимать это и быть готовым с Планом Б для ее решения

• После того, как вы правильно решили проблему, вам следует вернуться и посмотреть на процесс. Найдите минутку, чтобы поразмыслить над проблемой и методом, с помощью которого вы ее решили. Это поможет определить концепции, которые вам нужно изучить во время практики.

— Статья Судханшу Синхала, управляющего директора Sinhal Classes Pvt. ООО

Прочтите: CBSE Class 12 Mathematics: Экзаменатор совета указывает 8 распространенных ошибок, мешающих студентам получить полные 100

Прочтите: CBSE Class 10 Mathematics Board Exam 2018: Решите образец работы здесь !

Прочтите: Математика, основанная на развлечениях и занятиях! Этот новый метод может сделать изучение математики интересным

Что такое правильная установка для решения математических задач ?: Написание арифметических выражений — видео и стенограмма урока

Надевание математических меток

Первый шаг в правильной постановке нашей задачи с математическими словами — это пометить важные части задачи.Под важными я имею в виду те части проблемы, которые нам нужно использовать для решения проблемы. Как мы узнаем, что это такое? Мы начинаем с поиска ответа, который хочет решить проблема. В нашей задаче проблема заключается в том, чтобы узнать общую сумму, заработанную в конце недели. Я продолжаю и выделяю фразу, которая гласит: сколько денег он должен потратить в конце одной недели. Затем я думаю о том, что мне нужно, чтобы вычислить этот ответ. Что ж, мне нужно знать, сколько он работал и сколько зарабатывает. Проблема подсказывает мне, что он зарабатывает 12 долларов.50 в час. Я могу выделить эту часть. Проблема также говорит мне, что он работает 5 часов в субботу и 3 часа в пятницу. Я продолжаю и выделяю эту информацию. Мне нужно что-то еще решить? Нет, поэтому я могу игнорировать другие слова в задаче.

Теперь я могу обозначить эти части проблемы. Я собираюсь пометить то, что я ищу, мой ответ, размером x . Я пишу это x рядом с выделенной частью проблемы, которая говорит мне, что нужно решать.Я могу сократить до «S», чтобы обозначить заработок за субботу, и «F», чтобы обозначить доход за пятницу.

Написание математического выражения

Я закончил с разметкой, и теперь мне нужно написать математическое выражение, которое позволит мне легко решить задачу. Эта часть требует некоторого размышления, но оно того стоит!

Я начинаю писать математическое выражение, записывая x = так как я знаю, что мой ответ что-то равняется. Я поставил x для своей части ответа, которую я пометил, и поставил знак равенства, чтобы сообщить мне, что мне нужно что-то решить, чтобы найти свой ответ.Что идет после знака равенства? Что ж, проблема хочет знать, сколько Джеймс зарабатывает за неделю. Если Джеймс работает только по пятницам и субботам, то общая сумма заработка за неделю будет равна его заработку за пятницу плюс его заработок за субботу. Я уже обозначил эти части проблемы, поэтому я собираюсь записать эти ярлыки. Я могу написать «пятничный доход» или «F», и я могу написать «субботний доход» или «S». Я поставил знак плюса между этими двумя частями, чтобы сообщить, что мне нужно сложить их вместе.Итак, теперь мое математическое выражение выглядит так: x = F + S. Но что такое F и S? Если Джеймсу платят 12,50 долларов в час, то сумма, которую он зарабатывает каждый день, зависит от того, сколько часов он работает. Мне нужно умножить его заработок на количество часов, которые он работает. Для пятницы это будет 12,50 долларов * 3, а для субботы — 12,50 долларов * 5. Итак, я могу заменить букву F на 12,50 долларов * 3, а букву S на 12,50 долларов * 5. Теперь у меня есть математическая задача x = 12,50 долларов * 3 + 12,50 долларов * 5.

Решение проблемы

Кажется, эту проблему легко решить, не так ли? Все, что мне нужно сделать, это произвести умножение и сложить результаты.Это совсем не плохо. Позвольте мне пойти дальше и посмотреть, какой я получу ответ. Умножение 12,50 доллара на 3 дает мне 37,50 доллара, а умножение 12,50 доллара на 5 дает 62,50 доллара. Теперь мне нужно сложить их, чтобы получить 100 долларов. И угадай что? Я решил свою проблему. Джеймс зарабатывает 100 долларов в конце недели, и именно столько денег он должен потратить в конце недели.

Сводка урока

Вы можете увидеть, как правильная постановка задачи по математике упрощает решение конечного ответа.Самое сложное — это написать математическое выражение, но, немного подумав, это можно сделать. Как только это будет сделано, остальное легко!

Мы узнали, что правильный способ постановки задачи по математике состоит в выполнении определенных шагов.

1. Пометьте важные детали. Сначала вам нужно выяснить, в чем проблема, а затем подумать над информацией, которая вам нужна, чтобы найти ответ. Вы выделяете эти части проблемы. Затем вы наклеиваете на них ярлыки, чтобы упорядочить их и не позволить запутать вас.Используйте описательные фразы или буквы. Я обычно обозначаю ответ как x , чтобы отделить его от всех остальных ярлыков.

2. Напишите математическое выражение, которое нужно решить. После того, как вы все пометили, пришло время написать математическое выражение. Вы начинаете с x =, а затем записываете другие метки, используя правильную математическую операцию, чтобы найти свой ответ. Эта часть требует некоторого размышления, чтобы знать, как расположить метки и какую математическую операцию поставить. Подумайте о своем базовом сложении, вычитании, умножении и делении.Вы знаете, что делают эти операции, поэтому не задумывайтесь над проблемой. Для этикеток запишите для них важные числа, как мы это сделали с нашей проблемой.

3. Решите математическое выражение. Когда вы закончите писать математическое выражение, вашим следующим и последним шагом будет его решение. Следуйте своему порядку действий, чтобы решить и получить ответ.

Результаты обучения

После просмотра этого видеоурока вы должны уметь делать следующее:

• Обозначьте различные части математической задачи со словами
• Решите математические задачи со словами, выполнив серию шагов

Решение задач по математике

Основная причина изучения математики — научиться лучше решать проблемы во всех сферах жизни.Многие проблемы являются многоступенчатыми и требуют определенного систематического подхода. При решении проблем вам нужно сделать несколько вещей. Спросите себя, какой именно тип информации запрашивается: сложение, вычитание, умножение или деление? Затем определите всю информацию, которую вам дают в вопросе.

Книга математика Джорджа Полиа «Как решить: новый аспект математического метода», написанная в 1957 году, — отличное руководство, которое стоит иметь под рукой.Приведенные ниже идеи, которые предоставляют вам общие шаги или стратегии решения математических задач, аналогичны идеям, изложенным в книге Полиа, и должны помочь вам распутать даже самую сложную математическую задачу.

Используйте установленные процедуры

Научиться решать задачи по математике — значит знать, что искать. Математические задачи часто требуют установленных процедур и знания того, какую процедуру применять. Чтобы создать процедуры, вы должны быть знакомы с проблемной ситуацией и уметь собирать соответствующую информацию, определять стратегию или стратегии и надлежащим образом использовать эту стратегию.

Решение проблем требует практики. Принимая решение о методах или процедурах, которые следует использовать для решения задач, в первую очередь вы будете искать подсказки, что является одним из самых важных навыков при решении задач по математике. Если вы начнете решать проблемы с поиска ключевых слов, вы обнаружите, что эти слова часто указывают на операцию.

Ищите слова-подсказки

Считайте себя математическим детективом. Когда вы сталкиваетесь с математической задачей, первое, что нужно сделать, — это поискать ключевые слова.Это один из самых важных навыков, который вы можете развить. Если вы начнете решать проблемы с поиска ключевых слов, вы обнаружите, что эти слова часто указывают на операцию.

Общие ключевые слова для проблем со сложением:

• Сумма
• Всего
• Всего
• Периметр

Общие ключевые слова для задач на вычитание:

• Разница
• Сколько еще
• Превышает

Общие ключевые слова для задач умножения:

Общие ключевые слова для проблем с разделением:

• Поделиться
• Распределить
• Частное
• Среднее значение

Хотя ключевые слова будут немного отличаться от проблемы к проблеме, вы скоро научитесь распознавать, какие слова означают и что, чтобы выполнить правильную операцию.

Внимательно прочтите проблему

Это, конечно, означает поиск ключевых слов, как описано в предыдущем разделе. Определив ключевые слова, выделите или подчеркните их. Так вы узнаете, с какой проблемой вы столкнулись. Затем сделайте следующее:

• Спросите себя, видели ли вы проблему, подобную этой. Если да, то что в нем похожего?
• Что вам нужно было сделать в этом случае?
• Какие факты вам сообщают об этой проблеме?
• Какие факты вам еще нужно узнать об этой проблеме?

Разработайте план и проанализируйте свою работу

Основываясь на том, что вы обнаружили, внимательно прочитав проблему и определив похожие проблемы, с которыми вы сталкивались ранее, вы можете:

• Определите вашу стратегию или стратегии решения проблем.Это может означать выявление закономерностей, использование известных формул, использование эскизов и даже предположение и проверку.
• Если ваша стратегия не работает, это может привести вас к моменту ага и к стратегии, которая действительно работает.

Если кажется, что вы решили проблему, задайте себе следующие вопросы:

• Ваше решение кажется вероятным?
• Отвечает ли он на первоначальный вопрос?
• Вы ответили, используя язык вопроса?
• Вы ответили, используя те же единицы измерения?

Если вы уверены, что ответ «да» на все вопросы, считайте, что ваша проблема решена.

Советы и подсказки

Некоторые ключевые вопросы, которые следует учитывать при приближении к проблеме, могут быть следующими:

1. Какие ключевые слова в проблеме?
2. Нужен ли мне визуальный элемент данных, например диаграмма, список, таблица, диаграмма или график?
3. Есть ли формула или уравнение, которые мне понадобятся? Если да, то какой?
4. Нужно ли мне пользоваться калькулятором? Могу ли я использовать или следовать шаблону?

Внимательно прочтите проблему и выберите способ ее решения.Когда вы закончите работу над проблемой, проверьте свою работу и убедитесь, что ваш ответ имеет смысл и что вы использовали те же термины и / или единицы в своем ответе.

Порядок операций — Бесплатная математическая справка

Введение

Порядок операций — очень простая концепция, жизненно важная для правильного понимания математики. В отличие от чтения, где мы всегда работаем слева направо, иногда с математикой нам нужно проработать одну часть задачи перед другой, иначе окончательный ответ может быть неверным! Мы используем термин «порядок операций», чтобы описать, с какой частью проблемы нужно работать в первую очередь.Возьмем, к примеру, это уравнение:

$$ 4 + 6 \ div 2 * 11 =? $$

Если бы вы просто решали слева направо, ответ был бы неверным. Давайте сделаем это сейчас: 4 + 6 = 10. Разделите это на 2, чтобы получить 5. Умножьте 5 на 11, чтобы получить 55. К сожалению, хотя это казалось нормальным, этот ответ неверен.

Правильный порядок действий

Порядок действий позволит вам решить эту проблему правильно. Порядок следующий: Круглая скобка , Экспонентов , Умножение и деление и, наконец, Сложение и вычитание .Всегда сначала выполняйте операции внутри круглых скобок, а затем выполняйте операции с показателями. После этого выполните все умножение и деление слева направо и, наконец, все операции сложения и вычитания слева направо.

Популярным способом запоминания порядка является аббревиатура PEMDAS. Круглые скобки, экспоненты, умножение и деление, сложение и вычитание. Вы также можете создать небольшую фразу, например: « P lease E xcuse M y D ear A Unt S ally.«Что бы вы ни выбрали, убедитесь, что вы хорошо знаете все шесть этапов порядка операций.

Давайте попробуем решить это уравнение еще раз, на этот раз с помощью PEMDAS.

$$ 4 + 6 \ div 2 * 11 =? $$

Шаг 1) Круглые скобки. Нет ни одного. Двигаться дальше.

Шаг 2) Показатели. Никто. Продолжай …

Шаг 3) Умножение и деление. Идите слева направо, выполняя все операции умножения и деления, когда вы сталкиваетесь с этим, поэтому разделите 6 на 2, чтобы получить 3, и умножьте это на 11, чтобы получить 33.2 \ div 5 $$ $$ 5 + 144 \ div 5 $$ $$ 5 + 28,8 $$ 33,8 $ $

К настоящему моменту вы должны иметь базовое представление о порядке операций. Чтобы продолжить изучение этой темы, вы можете продолжать просматривать наш сайт или попробовать поискать в Интернете на Yahoo или Google. MathGoodies.com также предлагает отличный урок о порядке операций.

Как решать математические задачи со словами

Математические задачи со словами могут быть болезненными. И не только в том, что «я эмоционально устал» болезненно.Мы говорим о том, что «у меня болит голова, я истощен, это потребовало слишком много работы, я не знаю, что будет дальше, я эмоционально устал», и это довольно болезненно.

И дело не в том, что во время учебы можно каким-то образом избежать математических задач со словами. Ты не можешь. Они всегда будут рядом. А математику всегда нужно изучать в школе.

Не позволяйте задачам по математике вызывать у вас головную боль. Используйте эти простые шаги, чтобы с легкостью решить любую задачу с математическим словом (ну, настолько же легко, насколько это возможно при решении математических задач.Мы понимаем — это никогда не бывает полностью легко. Это математика…).

1. Познакомьтесь с математической задачей со словами

Существует интересная разница между математическими задачами со словами и простым решением уравнения : математические задачи со словами не дают вам уравнения.

Вместо этого они вызывают у вас головную боль. Так много математики связано с правильным решением уравнений. Если у вас нет уравнения, его сложно решить.

Это означает, что у вас есть несколько шагов, прежде чем вы сможете решить свою математическую задачу со словами.Но прежде чем мы попытаемся разобраться в ней, лучше всего просто попытаться выяснить, в чем проблема — вообще говоря. Просто узнай о проблеме. Прочтите его один или два раза. На этом этапе вам не нужно во всем разбираться — просто пожалуйте проблему. Вы не решите ее, пока хотя бы не ознакомитесь с ситуацией.

2. Ответьте на 3 вопроса о конкретной математической задаче со словами:

После того, как вы немного узнаете о стоящей перед вами проблеме, мы зададим ей три вопроса.Вы можете задать эти три вопроса по любой проблеме со словами, по любому типу математики. Это простой процесс, но он разберет все важные элементы любой математической задачи.

а) Что я ищу?

Это самый большой вопрос. Он формирует все ваше время, отвечая на вопрос. Возьмем, к примеру, следующую ситуацию:

Самолет вылетает из Торонто, Онтарио (Канада), направляется в Ньюарк, штат Нью-Джерси, а затем направляется в Сиэтл, штат Вашингтон. По пути в Сиэтл шторм вынуждает самолет направиться на север, чтобы его обойти.Самолет пересекает границу с Канадой, но затем у него проблемы с двигателем. Когда самолет находится на высоте 30 000 футов, выходит из строя двигатель, и ему приходится совершать вынужденную посадку. К сожалению, самолет разбивается… и это происходит прямо на канадско-американской границе. Где хоронят выживших?

Мы дадим вам подумать над этим вопросом несколько минут. Если вам интересно, вы можете увидеть ответ внизу этого сообщения. Но я рекомендую перепроверить самую важную деталь, прежде чем вы угадаете: «Что я ищу?»

Не теряйтесь в деталях.Задайте вопрос прежде всего. Вы должны знать, о чем спрашивает ваша математическая задача.

Если вы не знаете, что ищете, вы будете каждый раз это упускать.

б) Что мне нужно, чтобы найти ответ?

После того, как вы узнаете, о чем вас спрашивают, вы можете подумать, что нужно сделать, чтобы получить ответ. На этом этапе у вас должно быть некоторое представление об уравнении, которое понадобится для поиска решения.

В частности, здесь мы говорим об уравнениях и наиболее важных переменных.

Если вы знаете, что ищете, и затем можете назвать элементы, которые вам нужно найти, даже самые сложные проблемы станут чрезвычайно решаемыми.

Для простого примера допустим, что вам задали вопрос и вы понимаете, что вас спрашивают, какой высоты лестница вам понадобится, чтобы покрасить стену (я знаю, странная проблема, но просто согласитесь).

Узнав, о чем вас просят — о длине лестницы, — вы понимаете, что для ее решения вам понадобится теорема Пифагора.Это означает, что наш последний вопрос, необходимый для решения этой математической задачи со словами, будет очень простым.

c) Что у меня уже есть?

Вы знаете вопрос. Вы знаете, что вам нужно, чтобы решить эту проблему. Теперь вы можете просто заполнить уравнение тем, что вам уже было дано.

Не теряйтесь в мелочах. Математические задачи со словами печально известны тем, что дают вам слишком много деталей. Вот почему этот шаг — последний из трех вопросов.

Некоторые студенты сначала пытаются выяснить, что у них есть.Они читают проблему, записывают все детали, которые им были даны, а затем ожидают решения ее оттуда. Вместо этого они часто испытывают перегрузку деталями.

Но вы сэкономите огромное количество времени, если будете знать, что сначала хотите ответить. Знать вопрос важнее, чем знать, какие детали у вас есть. Только когда вы знаете вопрос, на который отвечаете, и то, что вам нужно для ответа, вы сможете найти нужные детали, чтобы ответить на него правильно.

3.Подключи и забей

Вы, наверное, догадались об этом шаге. Вы знаете правильный вопрос. Вы знаете правильное уравнение. Вы нашли нужную информацию.

Подключи и давай. Просто введите свои значения в уравнение и получите правильный ответ, решив проблему.

Не забудьте пометить и свой ответ! Если вы знаете, что ищете, ваш ответ должен быть в правильных единицах. Но всегда целесообразно перепроверить.

Сообщите нам, что вы думаете! Вот как вы решаете математические задачи со словами?

(Ищете ответ на вопрос Канада-Соединенные Штаты? Ну, ответ нигде. выживших не хоронить )

Чтение и понимание письменных математических задач

Словесные задачи в математике часто представляют собой проблему, потому что они требуют, чтобы учащиеся прочитали и поняли текст задачи, определили вопрос, на который необходимо ответить, и, наконец, создали и решили числовое уравнение. Многие ELL могут испытывать трудности с чтением и пониманием письменного содержания в текстовой задаче. Если студент изучает английский как второй язык, он может еще не знать ключевой терминологии, необходимой для решения уравнения.Другими словами, ELL, получившие формальное образование в своей стране, обычно не испытывают математических трудностей; следовательно, их борьба начинается, когда они сталкиваются со словесными проблемами на втором языке, который они еще не освоили (Bernardo, 2005). По этой причине рекомендуется, чтобы студенты выучили ключевую терминологию, прежде чем пытаться решать математические задачи со словами.

Ключевые преимущества

Когда изучающие английский язык выучат ключевую терминологию, используемую в математических задачах со словами, им будет легче научиться писать числовые уравнения.Учителям важно предоставить учащимся ELL возможность выучить и практиковать ключевые слова из словарного запаса.

Ключевые слова очень важны, но они — только часть процесса. Понимание языка в текстовых задачах имеет решающее значение для всех учащихся. Им нужно знать значение слов. Но поскольку слова часто используются по-разному и проблемы ставятся по-разному, есть некоторые предостерегающие сообщения. Вот пример задачи, в которой для построения уравнения вычитания используется «меньше».

У Марии 24 шарика, что на 8 меньше, чем у Паоло. Сколько шариков у Паоло? Если бы мы сосредоточились только на ключевых словах, «меньше, чем» было бы сигналом для выбора чисел и вычитания. Учащийся может сразу сделать вывод, что ответ — 16, но проблема не в этом, и ребенок будет неправ. (Правильный ответ, кстати, 32).

Исследование показало, что если мы попросим студентов полагаться только на знание того, что определенные ключевые слова сигнализируют о конкретных операциях, мы фактически можем увести их от попыток понять проблемы.Они будут искать только эти слова и любые числа в задаче, даже если они не имеют отношения к ответу. Это не поможет им впоследствии овладеть математикой, даже если они хорошо владеют английским языком.

Хотя поиск ключевых слов проводился с обычными студентами, последствия для студентов ELL, если они полагаются на них, такие же. Они не смогли бы решить указанную выше проблему. Однако, если учителя будут следовать предложенному процессу чтения задачи несколько раз (как в младших, так и в старших классах) и обсуждать, что это означает, ученики поймут.Еще один хороший инструмент — научить их рисовать или моделировать проблемы. Чтобы проиллюстрировать проблему выше, вы могли бы сказать: «Вот 24. Марии». Затем нарисуйте 24 единицы, фигуры, формы и т. Д., Чтобы представить 24. «Вот Паоло; у него больше, потому что у Марии меньше, чем у него». Нарисуйте 24 единицы, фигуры, формы и т. Д., Чтобы получить 24, и добавьте еще 8. «Значит, у Паоло должно быть больше 24. Сколько еще? 8. Так каково общее количество Паоло?»

Разница между знанием значения слов «меньше чем» и использованием «меньше чем» в качестве ключа к операции.Мы хотим, чтобы учащиеся знали значение слов, но также видели их в контексте всей проблемы.

Предлагаемые занятия

Младшие классы

Практикуйтесь в решении проблем ежедневно, просто задавая больше вопросов. Например:

• Сколько учеников принесли сегодня домашнее задание?
• Сколько еще детей принесли вчера домашнее задание?
• У нас на доске было 8 маркеров, а теперь их всего 3. Сколько мы убрали?
• Сколько животных в этом журнале? Сколько млекопитающих? Сколько птиц? (введение в дроби и проценты)

Продолжайте ежедневно использовать ключевую терминологию и помещать ее в контекст (например,г., меньше, больше, разница, раз, каждый и т. д.). Покажите студентам, как легко можно неправильно понять проблему.

Старшие классы

• Прочитайте текстовые задачи медленно и внимательно несколько раз , чтобы все учащиеся их понимали.
• Если возможно, разбейте проблему на более мелкие сегменты.
• Позвольте учащимся разыграть словесные задачи, чтобы лучше понять, что их просят решить.
• Предоставьте ученикам манипуляторы, чтобы помочь студентам визуализировать проблему.
• Совершите полевые или пешие прогулки, чтобы определить расстояния, скорость, пройденную территорию и т. Д.
• Попросите учащихся провести опросы, интервью, практические исследования в реальных ситуациях, чтобы вычислить проценты, различия и математические вычисления более высокого порядка навыки и умения.
• Позвольте учащимся рисовать рисунки или диаграммы, чтобы помочь им понять проблемы.

Как решить вирусную математическую задачу 2019

Вот оно появилось в Твиттере, как жестокая насмешка:

Этот контент импортирован из Twitter.Вы можете найти тот же контент в другом формате или найти дополнительную информацию на их веб-сайте.

Каждые несколько месяцев Интернет пожирает себя какой-нибудь вирусной загадкой или иллюзией, каждая из которых выводит из себя больше, чем предыдущая. И так, как по маслу, эта сводящая с ума математическая задача стала вирусной, следуя великой традиции таких травмирующих событий, как «Платье» и «Янни / Лорел».

Загадки такого рода преднамеренно предназначены для разделения и подчинения, и, как и ожидалось, кажущаяся простая проблема, поставленная в оскорбительном твите — 8 ÷ 2 (2 + 2) — на практике вызвала гражданскую войну в офисе Popular Mechanics . которыми мы также делимся с нашими (бывшими) друзьями в журналах Runner’s World и Bicycling .

➗ Вы любите сложные математические задачи. И мы тоже. Решим их вместе.

Естественно, мы обратились к Slack, чтобы выявить наши различия. Вот горячая беседа между редакторами, которые перестали делать хоть какое-то подобие реальной работы в течение дня, чтобы решить уравнение, созданное, чтобы сбить с толку четвероклассников — и нажить много врагов в процессе, — за которым следует понимание реальных математиков и физиков, которые неохотно откликнулись на нашу просьбу за комментарий, чтобы раз и навсегда разрешить яростные математические дебаты.

The Slack War, Часть I

Дерек Колл, видеопродюсер: 8 разделить на 8 равно 1.

Джефф Денгейт, Runner’s World Главный бегун: PEMDAS. 16.

Бобби Ли, редактор тестов (и трехкратный олимпийский велосипедист): Я езжу на велосипедах

Пэт Хайне, продюсер видео: … она записывает PEMDAS, а затем PEDMAS

Matt: Вы явно не слушали

Pat: Я не слушал…я была занята исправлением своей математики.

Дерек: Когда они изобретают математику заново?

Мэтт: хорошо, Дерек, видео для вас

Пат: если вы получили 16, это потому, что вы не знаете разницы между скобками и скобками.

Википедия

Морган Петруни, редактор тестирования: Я согласен с Дереком и не согласен с YouTube. Что, если вы хотите проделать долгий путь и использовать свойство распределения, а сначала распространить 2? Вы бы сделали: 8 / (4 + 4) = 1.

Или дистрибутивное свойство вдруг перестало действовать?

Это то, что я бы сказал, доказывает, что 1 правильный.

Дерек: Я доверяю Морган, потому что в это десятилетие у нее был математический класс.

Pat: Википедия говорит, что вы ненавидите Америку, если получаете 16.

Википедия

Дэн Роу, редактор теста: Верно, но это умножение / деление, а не умножение, а затем деление

Морган: НО умножение с круглыми скобками превосходит деление.Так что у вас все еще остается 8/2 (4). Так что сначала вам нужно сделать 2х4. По крайней мере, так меня учили.

Дэн: умные люди из Беркли говорят, что это слишком двусмысленно, чтобы говорить; PEMDAS — это не математическая конвенция, а метод обучения

Pat: умножение / деление :: правильно / неправильно

Тейлор Ройек, помощник редактора функций: Главный вывод не в том, что кто-то плохо разбирается в математике, но этот человек не умеет писать четкие уравнения

Билл Стрикленд, редакторский директор : СДЕЛАЙТЕ ЭТО СОДЕРЖАНИЕ!

инстаграм-история, в которой наши сотрудники обсуждают?

можно назвать известного математика?

Бобби: Звучит как разговор, относящийся к сегменту «Не моя работа» Подожди, подожди, не говори мне

Кэти Фогель, редактор социальных сетей: сейчас опрашивает нашу аудиторию IG по этому поводу…

Pat: Уравнение написано не в соответствии со стандартами ISO, что оставляет неоднозначность интерпретации, и настоящий ответ заключается в том, что нам нужно научить лучше писать математику.

Неоднозначный PEMDAS

Неоднозначные проблемы, порядок операций, PEMDAS, BEMDAS, BEDMAS

он же … то, что сказал Тейлор, но из Гарварда

Морган: он же … научить распределительному свойству вместо случайных сокращений

Pat: Если написано в соответствии со стандартом ISO, ответ — 1.

Пэт Хайне

Эндрю Дэниэлс, редактор с практическими рекомендациями: честно, мы могли бы опубликовать эту слабую ветку слово в слово, а затем попросить ученого присоединиться к нам и обучить нас

Кэти Фогель: Из нашей аудитории IG …

Кэти Фогель / Instagram

Кит Фокс, редактор специальных проектов: Разве здесь не вопрос и двусмысленность, когда исчезают круглые скобки? Мол, остаются ли парены после того, как ты сделаешь 2 + 2? Или они исчезнут, как только вы сначала решите мини-уравнение внутри скобок.Я говорю, что они никуда не денутся. Я в команде 1

Я также не посещал математические классы более 10 лет

Тревор Рааб, фотограф: Мой вопрос: к какому сценарию реального мира это применимо к

Брэд Форд, редактор теста: Класс математики?

Тревор: ах, классический учись математике, чтобы научиться больше заниматься математикой

Бобби: школа — не реальный мир

Морган: Создание горячих и поляризационных офисных дискуссий

Брэд: Бобби, скажи это шестикласснику.

Бобби: Сейчас я буду работать над подготовкой аргументации

Тейлор: У вас есть, что, 11 лет, чтобы усовершенствовать его

Бобби: Время на моей стороне

это код для: Я могу отложить это на очень долгое время

Пат: , который является кодом для «спроси свою мать»

Бобби: она любит утверждать, что она хороша в математике. Она может пожалеть о том дне, когда хвасталась этим

Pat: «Это не поможет мне выиграть миллионы долларов в Fortnite, хотя»

Краткое заявление Майка Брина, сотрудника по общественной осведомленности Американского математического общества , Чья работа — «рассказывать людям, насколько хороша математика»

Согласно порядку операций, вы сначала решаете то, что указано в скобках.Это дает вам 4. Затем в PEMDAS умножение и деление имеют равный приоритет, поэтому вы должны делать первое, что происходит слева направо. Итак, сначала нужно разделить 8 на 2, то есть 4. Таким образом, получится 16 в соответствии с классическим порядком операций.

Но как написано, неоднозначно. В математике часто возникают двусмысленности. Математики стараются делать правила как можно точнее. По строгому порядку действий у вас будет 16, но я бы не стал бить кого-нибудь линейкой по запястью, если он скажет 1.

The Slack War, часть II

Эндрю: ууууу мальчик

я только что разговаривал по телефону с американским математическим обществом

какие американские горки это оказывается

мой человек микрофон с AMS, чья работа состоит в том, чтобы прямо отвечать на подобные вопросы, говорит, что ответ таков …

Брэд: 42

Тайлер Дасвик, помощник редактора функций: тайно лучший ответ здесь

Эндрю: ШЕСТНАДЦАТЬ

Эндрю, минут спустя: , почему никто не реагирует должным образом на эту новость

Брэд: Потому что он неправ.

Тревор: , но разве это не противоречит PEMDAS?

Эндрю: он говорит (и мне придется вернуться к стенограмме), что при использовании * традиционного * порядка операций ответ будет 16

Мэтт Филлипс, старший редактор теста: Эндрю, у моего брата есть имеет степень доктора теоретической физики и пишет статьи с такими названиями, как… «Угловая зависимость для ν ‘, j’-разрешенных состояний в реактивном рассеянии F + h3 → HF (ν’, j ‘) + H с использованием нового источника пучка атомного фтора» I может посмотреть, хочет ли он взвесить…

Андрей: да! пожалуйста, сделайте [Примечание редактора: брат Мэтта не ответил.]

Тейлор: есть ли способ, которым 1 также является правильным ответом на этот вопрос?

Тревор: PEMDAS

Эндрю: Я также отправлю запрос своему физику, который также только что ответил на вопрос POP о том, как прыгнуть с движущегося поезда

Тейлор: tbh, это было бы было бы здорово, если бы мы смогли найти экспертов, которые не согласны.

Тревор: , подождите, вернул мою интерпретацию PEMDAS обратно к 16

вот почему я пошел в художественную школу

Тейлор: Я спросил своего друга [УДАЛЕНО], кто такой собирается закончить университет с докторской степенью по статистике из [УДАЛЕНО], имеет три или четыре степени магистра математики

, и я так рад сообщить, что она на моей стороне

Тейлор Ройек

Дерек: [УДАЛЕНО] выигрывает

Эндрю: но что [УДАЛЕНО] было ответом ??!

Тейлор: нет ответа, фальшивый вопрос, созданный, чтобы разжечь возмущение

Билл: , может быть, наш умный подход таков: математика не субъективна, никто не пишет математику таким образом, вот что не так

Тейлор: она только начинает

Тейлор Ройек

Комплект: Похоже, [УДАЛЕНО] нужно написать потную математику. Take

Эндрю: daaaaang [УДАЛЕНО]

go off

Бобби: нет, мы на что-то наткнулись!

Прощальный выстрел от Ретта Аллена, доктора философии.D., доцент кафедры физики в Университете Юго-Восточной Луизианы, вынесший окончательный вердикт и решительно закрыл нас всех

Это математическая версия: «Какого цвета это платье? Синий и черный или золотой и белый? »Я отвечу, что сначала вы ставите скобки, так что получается:

8/2 * 4

Затем вы идете слева направо.

8/2 равно 4, поэтому это

4 * 4

Теперь вы получаете 16.

Конечно, это не математика. Это условность.У нас есть соглашения о том, как писать эти вещи, точно так же, как у нас есть соглашения о том, как писать что-то по буквам. Но все же есть разные условности. Некоторые люди пишут это как «серый», а другие как «серый». Мы все еще понимаем, что происходит. Что касается меня, я бы написал это более подробно, чтобы не было путаницы. Как это:

8 / (2 * (2 + 2)), если это то, что вы пытаетесь сделать. Таким образом, никто не ошибется.

Футболки Popular Mechanics на Amazon

Футболка с обложки Popular Mechanics, апрель 1940 г.

Футболка на обложке Popular Mechanics, январь 1951

Футболка с обложкой журнала Popular Mechanics, июль 1982 года

Футболка с обложкой Popular Mechanics, октябрь 1943 г.

Футболка на обложке Popular Mechanics, март 1936 года

Футболка с обложкой журнала Popular Mechanics, июнь 1935 года

Футболка с обложкой Popular Mechanics, ноябрь 1923

Футболка с обложкой Popular Mechanics, ноябрь 1922

Футболка с обложкой Popular Mechanics, январь 1994

Футболка на обложке Popular Mechanics, апрель 1915 года

Футболка с обложкой Popular Mechanics, январь 1931

Футболка с обложкой журнала Popular Mechanics, июнь 1926 года

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты.