Задачи в два действия — урок. Математика, 2 класс.
Карлсон за один день съел \(10\) банок варенья, а за второй день съел на \(3\) банки меньше. Сколько всего банок варенья съел Карлсон за два дня вместе?
По условию составим запись и выработаем план решения:
1 день −10 банок 2 день −? на 3 банки меньше, чем в 1 день − за 2 дня вместе?
Обрати внимание!
Анализируя эту схему, делаем вывод, что задача решается двумя действиями.
Сначала найдём ответ на вопрос:
1) сколько банок варенья съел Карлсон за второй день?
На \(3\) банки меньше — это значит, следует отнять \(3\)!
\(10 — 3 = 7\) (б.) — столько банок варенья съел Карлсон за второй день.Теперь знаем количество банок варенья, которое съел Карлсон за первый день и за второй день. Поэтому можно ответить на вопрос задачи.
2) Сколько всего банок варенья съел Карлсон за два дня вместе?
Вместе — это значит, следует сложить!
\(10 + 7 = 17\) — столько банок варенья съел Карлсон за два дня вместе.
Ответ: за \(2\) дня Карлсон съел \(17\) банок варенья.
Можно решение этой задачи записать и одним примером:
\((10 — 3) + 10 = 17\).
Первым действием в скобках ответим на первый вопрос, а вторым действием ответим на вопрос задачи.
Пример:
в клетке было \(7\) синих попугаев и \(8\) зелёных попугаев.
Продали \(5\) птиц. Сколько попугаев осталось в клетке?
Сразу на вопрос задачи ответить нельзя.
В ходе решения составим такую запись:
1) \(7 + 8 = 15\) п.,
2) \(15 — 5 = 10\) п.
Ответ: \(10\) попугаев осталось в клетке.
Первым действием узнали общее количество птиц в клетке.
Вторым действием ответили на вопрос задачи, т. е. узнали количество попугаев, оставшихся в клетке.
Задачи в два действия — это составные задачи, в которых для нахождения искомого ответа нужно сначала вычислить одно неизвестное по имеющимся данным.
Задание 11. Текстовые задачи — профильный ЕГЭ по математике.
Задание 11 Профильного ЕГЭ по математике – это несколько типов текстовых задач. Условия и «сюжеты» задач могут быть разными. При этом в каждой из них нужно построить математическую модель, то есть обозначить какие-либо величины за переменные, составить уравнение и решить его. И еще есть неочевидные секреты их решения. О них – в конце статьи.
Вот основные типы текстовых задач, которые могут вам встретиться на ЕГЭ под номером 11. Переходите по ссылкам, читайте краткую теорию и разбирайте вместе с нами решения задач!
1. Задачи на движение
2. Задачи на работу
3. Задачи на проценты
4. Задачи на сплавы, смеси, растворы
5. Задачи на движение по окружности
Формула работает и в этом случае. Здесь – расстояние, – скорость, – время.
А секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в -ный раз.
6. Задачи на нахождение средней скорости
По определению, средняя скорость получается, если всё расстояние поделить на всё время. В общем случае она не равна среднему арифметическому скоростей, а находится по следующей формуле:
7. Задачи на движение протяженных тел, встречное движение и обгон
Да, это те самые задачи, где поезд проходит через туннель. Или проезжает мимо платформы. И нам нужно учитывать длину поезда.
Есть еще задачи на встречное движение или обгон. Например, два поезда движутся навстречу друг другу (конечно, по параллельным путям), или один поезд обгоняет другой. Такие задачи удобно решать в движущейся системе отсчета.
Но и это не все. Есть еще задачи ЕГЭ на арифметическую и геометрическую прогрессии.
8. Задачи на арифметическую прогрессию
Арифметическая прогрессия в задачах ЕГЭ по математике
9. Задачи на геометрическую прогрессии
Задачи на геометрическую прогрессии
Геометрическая прогрессия в задачах ЕГЭ по математике
И еще мы обещали секреты решения текстовых задач на движение и работу. Читайте и применяйте!
Дар или навык? Что такое математические способности и как их развить
Успехи других людей – это всегда немного загадка. Почему у одних получается решать сложные математические задачи, а другие, как бы ни старались, не могут выйти на новый уровень? Неужели математика и правда подвластна не всем? На эти вопросы ответил Назар Агаханов, председатель Центральной предметно-методической комиссии по математике Всероссийской олимпиады школьников. С 1995 года руководил национальной командой России на международных математических олимпиадах.
В 2010 году Назар Хангельдыевич стал лауреатом премии Правительства РФ в области образования за научно-практическую разработку «Система развития всероссийских предметных олимпиад школьников, отбора и подготовки национальных сборных команд России на международные олимпиады по физике и математике». Когда проявляются математические способности, как их развивать и кому не стоит идти в олимпиадное движение – рассказал эксперт.
Фото: https://mipt.ru/
Математические способности – это умение построить новые модели, не повторяющие стандартные алгоритмы, которым научили в школе. На базе таких маленьких открытий и строятся наука и технологии. Именно поэтому математика позволяет находить способных детей.
Некоторые ученые считают, что порядка 10% людей обладают высокими математическими способностями. И это нормально. Если нет математических способностей, значит, есть что-то другое. Важно помогать детям открывать интересные сферы, но не навязывать.
«Каждый родитель хочет, чтобы его ребенок вырос успешным человеком, и сейчас очень популярна позиция, что развивать нужно с пеленок. Может быть, так и есть, но в любом случае лучше отталкиваться от искреннего интереса ребенка. Талант погибнет, если заставлять его делать несвойственное. Часто родители хотят использовать любые возможности, в частности, например, отправляют заниматься ментальной арифметикой, ложно полагая, что это шаг в математику, но это бессмысленная трата времени, ведь математика – это творчество. Не зря же задачи и решения называют красивыми»,
Может быть, так и есть, но в любом случае лучше отталкиваться от искреннего интереса ребенка. Талант погибнет, если заставлять его делать несвойственное. Часто родители хотят использовать любые возможности, в частности, например, отправляют заниматься ментальной арифметикой, ложно полагая, что это шаг в математику, но это бессмысленная трата времени, ведь математика – это творчество. Не зря же задачи и решения называют красивыми»,
Чаще всего склонность к математике начинает проявляться в начальной школе, но это не значит, что сразу нужно вести ребенка на несколько кружков и интенсивно развивать эти способности. Достаточно одного урока занимательной математики в неделю.
Более серьезные кружки начинают работу с учениками 5-6 классов. На этом этапе изучения математики обогнать сверстников очень легко. Круг задач еще достаточно узок и владение приемами их решения позволяет обойти даже, возможно, потенциально более сильных сверстников именно за счет знаний, а вот дальше, в 7-8 классах, для высоких результатов нужно чувствовать математику, здесь и проявляются математические способности. В это время преподаватели работают со школьником на развитие математического аппарата, укрепляется который уже в старших классах.
Поэтому нередко бывает, что ярко проявляющие себя в 5-7 классах школьники начинают терять свои позиции в старших классах и выгорают от непонимания, почему теперь не получается быть сильнее других. Хотя выгорание возможно и по другой причине – слишком долгие занятия олимпиадными задачами. Интерес все-таки нужно поддерживать, переключаясь на другую деятельность.
Характер и воля: что помогает добиваться успехов в олимпиадах
Трудолюбие и готовность много работать – наверное, самые очевидные качества, которые нужны в любой сфере для достижения высоких результатов.
«Способности – это фундамент. Чтобы подняться на несколько ступенек вверх, нужно работать. При наличии этих двух пунктов и еще хорошего педагога, все остальное уходит на второй план. Даже атмосфера в семье и материальное благополучие. В сборную часто попадают дети, у которых не очень устроено семейное положение. Можно даже сделать частный вывод, что чем больше благоустроен быт, тем меньше ребенок настроен трудиться», – рассказывает Назар Агаханов.
При наличии этих двух пунктов и еще хорошего педагога, все остальное уходит на второй план. Даже атмосфера в семье и материальное благополучие. В сборную часто попадают дети, у которых не очень устроено семейное положение. Можно даже сделать частный вывод, что чем больше благоустроен быт, тем меньше ребенок настроен трудиться», – рассказывает Назар Агаханов.
Еще один важный пункт, над которым нужно работать каждому олимпиаднику, – психологическая устойчивость. На олимпиаде ребенок от волнения может показать результат хуже, чем его потенциал. Более ярко это проявляется в спорте, когда ребенок, приезжая на международные соревнования, проваливается. Нужно уметь воспринимать состязания не как конкурс, где тебе придется преодолевать невероятные сложности, а как удовольствие от того, что ты встретишься с интересными задачами и попробуешь их решить. Самостоятельно психологическую устойчивость развивать сложно. Для этого важна среда.
«Задумайтесь, почему в хороших математических школах так много детей, показывающих высокие результаты? Во-первых, конечно, в лучших школах собираются лучшие учителя. Во-вторых, в конкурентной борьбе с равными тебе сверстниками ты привыкаешь – нужно доказывать, что ты лучший. Несколько раз сначала ты можешь сорваться из-за волнения, а дальше уже будешь спокоен»
Интересуйтесь всем: советы по эффективному олимпиадному тренингу
Если юный математик идет в олимпиадное движение только ради поступления в университет, лучше оставить эту затею. По словам эксперта, количество бюджетных мест по России определенно превосходит количество способных ребят, заканчивающих школы. Проблемы с тем, чтобы ребенок был талантлив в математике, а его не хотели брать на учебу в вуз, нет. Такие ребята с легкостью сдают экзамены. Повторимся, этот фактор абсолютно для математики не работает.
Пожалуй, нужно искренне любить соревноваться, чтобы спокойнее переживать возможный стресс. А педагог поможет раскрыть способности и стать лучше. Заниматься с преподавателями можно и онлайн, и оффлайн. Но эксперт уверен, что онлайн-формы не заменят личного общения.
А педагог поможет раскрыть способности и стать лучше. Заниматься с преподавателями можно и онлайн, и оффлайн. Но эксперт уверен, что онлайн-формы не заменят личного общения.
«Важен не объем пройденного материала, а то, как преподаватель послушал решение и рассуждения ребенка. Именно поэтому подготовка к международным олимпиадам во всех странах проходит примерно одинаково – учитель помогает разобрать ошибки, а не начитывает лекции. Школьник может увидеть решения тысяч задач и от этого не продвинуться, но, если он сам углубился в вопрос, попробовал решить, увидел трудные места, ему приоткроется новое знание. Дистанционные формы, к сожалению, в этом не столь эффективны, потому что важен живой диалог и прямая беседа. При этом место проживания – не крест для успехов. Хорошие преподаватели есть в регионах и это факт»,
Еще одна возможность прокачаться – различные турниры и летние школы, которые есть практически в каждом регионе. Можно подобрать для себя наиболее подходящие. Такие площадки собирают большое количество ребят из разных городов в одном месте, дают возможность и пообщаться, и вместе решать задачи, и познакомиться с педагогами, которые входят в жюри.
Еще один важный пункт на пути к эффективным занятиям – вовремя отдыхать. Спорт, прогулки, активный отдых – хороший инструмент для качественной перезагрузки между занятиями. Но не единственный.
«Большое количество открытий в математике происходит на стыке дисциплин, когда ты можешь переключиться, перенести свои способности на другое направление, в котором не являешься специалистом самого высокого уровня. Поэтому при стремлении добиться чего-то серьезного в математике, стоит интересоваться всеми предметами в школе и вообще разносторонне развиваться», – говорит Назар Агаханов.
Отсюда возникает вопрос, если тратить время на другие интересы, то сколько тогда нужно заниматься именно математикой? Конкретного ответа здесь нет, все очень индивидуально. Формулу поможет выработать внутреннее ощущение – заниматься нужно ровно столько, чтобы чувствовать, что ты находишься в форме. А вот перед олимпиадными турами важно не перегружать мозг слишком интенсивными занятиями, чтобы не устать.
Формулу поможет выработать внутреннее ощущение – заниматься нужно ровно столько, чтобы чувствовать, что ты находишься в форме. А вот перед олимпиадными турами важно не перегружать мозг слишком интенсивными занятиями, чтобы не устать.
Обрати внимание: самые распространенные ошибки начинающих олимпиадников
Многие начинающие олимпиадники делают ошибки из-за того, что не продумывают решение глубоко. Чаще всего это происходит из-за невнимательности и игнорирования части условий. Поэтому Назар Агаханов рекомендует, как банально бы это ни было, детально читать условия задач и использовать в решении все обозначенные параметры.
В решении геометрических задач чаще всего встречаются логические ошибки, когда то, что надо доказать, каким-то образом встраивается в логику решения. Пример: нужно доказать равенство углов. Школьник отталкивается от фразы «так как эти углы равны», решает задачу и попадает в логическую ловушку, делая некорректные выводы.
Распространенная ошибка в алгебре и комбинаторике – длинное решение с перебором вместо короткого. Решение методом перебора – нормальный подход, но, если пропускается какой-то случай, решение может не засчитаться, потому что именно в этом случае и было верное решение.
Олимпиадные задания (математика) – Олимпиада школьников «Высшая проба» – Национальный исследовательский университет «Высшая школа экономики»
В старых версиях браузеров сайт может отображаться некорректно. Для оптимальной работы с сайтом рекомендуем воспользоваться современным браузером.
Мы используем файлы cookies для улучшения работы сайта НИУ ВШЭ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь, наши правила обработки персональных данных – здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом НИУ ВШЭ и согласны с нашими правилами обработки персональных данных. Вы можете отключить файлы cookies в настройках Вашего браузера.
Вы можете отключить файлы cookies в настройках Вашего браузера.
Обычная версия сайта
2018/2019 учебный год
| Задания | Решения и критерии |
2019/2020 учебный год
Для младших классов: максимальная оценка за всю работу — 100 баллов. Если сумма баллов, набранных участником по всем задачам, превосходит 100, его итоговая оценка равна 100.
Для старших классов: итог подводится по трём задачам, по которым достигнуты наилучшие результаты; баллы за пункты одной задачи суммируются.
2018/2019 учебный год
| Задания | Решения и критерии |
2017/2018 учебный год
2016/2017 учебный год
2015/2016 учебный год
2014/2015 учебный год
2013/2014 учебный год
2012/2013 учебный год
Задания 8 класс (задачи 1 и 2 имеют вес 16 баллов, остальные — 17 баллов)
Задания 9 класс (все задачи имеют равный вес (кроме 4): 17 баллов, задача 4 — 15 баллов)
Задания 10 класс (все задачи имеют равный вес (кроме 2): 17 баллов, задача 2 — 15 баллов)
Задания 11 класс (все задачи имеют равный вес (кроме 3): 17 баллов, задача 3 — 15 баллов)
2011/2012 учебный год
Математика для младших школьников – СУНЦ МГУ
Данные курсы познакомят вас с задачами, которые традиционно относят к разделу олимпиадной математики. Но это не означает, что цель курсов – исключительно подготовка к олимпиадам. Решение нестандартных математических задач формирует умение логически рассуждать, способствует повышению интереса к математике, развитию математического мышления, познавательной активности, повышению математической культуры обучающихся. Чем раньше начать изучение олимпиадной математики, тем проще и интереснее будет учиться в дальнейшем.
Но это не означает, что цель курсов – исключительно подготовка к олимпиадам. Решение нестандартных математических задач формирует умение логически рассуждать, способствует повышению интереса к математике, развитию математического мышления, познавательной активности, повышению математической культуры обучающихся. Чем раньше начать изучение олимпиадной математики, тем проще и интереснее будет учиться в дальнейшем.
А еще сегодня умение решать олимпиадные задачи играет и другую важную практическую роль. Опираясь только на стандартную школьную программу, сложно поступить в хорошую физико-математическую школу (а набор нынче есть даже во 2 класс, но большая часть школ объявляет набор в 5 и 6 классы). Лучшие университеты страны набирают большую часть студентов на программы математической направленности по уровневым олимпиадам. Даже последние задачи из ЕГЭ по профильной математике требуют знаний некоторых тем олимпиадной математики.
Большинство тем наших курсов встречаются на вступительных испытаниях в различные школы России. Некоторые из наиболее сложных задач курсов ранее были включены в варианты известных математических соревнований. Данные дистанционные курсы были успешно опробованы автором на протяжении нескольких лет работы на Очных курсах СУНЦ МГУ.
В каждом курсе по 12 разделов. В каждом разделе 4 части:
- Видео-лекция и письменный конспект
- Задачи для тренировки с ответами
- Контрольная работа
- Решение контрольной работы
Особенности курса:
- Подробно разобраны все основные темы. На изучение каждой темы отводится около 2 недель. Наш курс – это не просто набор задач с последующими разборами. Это полноценные лекции с теоретическим материалом по каждой теме и примерами решения задач.
- Почти у каждой задачи есть несколько разных решений. В нашем курсе мы будем стараться обсуждать разные способы решения. Плохих решений не бывает – бывают неоптимальные.
- Крайне важно не только решить задачу, но и записать полностью обоснованное решение.
 В нашем курсе мы много внимания уделим именно записи решений. В каждом письменном конспекте приведены примеры оформления решений. Если в качестве решения контрольной работы присылать только ответы, то оценка будет низкой.
В нашем курсе мы много внимания уделим именно записи решений. В каждом письменном конспекте приведены примеры оформления решений. Если в качестве решения контрольной работы присылать только ответы, то оценка будет низкой.
Отметим, что письменный конспект может быть сложен для восприятия школьника младших классов. Именно поэтому все объяснения и разборы даны в виде видео-лекций, а конспект – это дополнение к видео.
Примеры материалов курса:
Этот курс входит в систему дистанционных платных курсов СУНЦ МГУ, пока нет возможности включить его в бесплатную заочную школу, которая работает только для школьников 7-11 классов.
Вся информация о том, как поступить на курсы, есть на странице https://internat.msu.ru/distantsionnoe-obuchenie/distance-courses/.
Если у Вас есть вопросы, то их стоит направлять на почту [email protected].
как сдать ОГЭ по математике — Учёба.ру
Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно
Ольга Евсеева,
преподаватель математики физико-математической школы Института довузовской подготовки
Московского технологического университета (МИРЭА, МИТХТ, МГУПИ)
По вашему мнению, насколько хорошо девятиклассники сейчас знают математику? Насколько сложен для них этот ОГЭ?
Не сказала бы, что школьники не знают математику. Как правило, к нам на занятия приходят ребята с неплохим начальным уровнем, с хорошими навыками выполнения арифметических действий и преобразования выражений, знакомые с методами решения линейных, квадратных уравнений и неравенств — то есть со всем тем, что они должны знать к началу 9 класса. Конечно, глубина знаний и умение ими пользоваться напрямую зависят от количества часов математики в школе: при изучении предмета на базовом уровне это три-четыре часа алгебры и два часа геометрии в неделю, на углубленном уровне — пять-семь часов алгебры и три часа геометрии. Поскольку ОГЭ состоит из двух частей, первая из которых проверяет базовый уровень подготовки, а вторая включает более сложные задания, ребятам, изучающим в школе базовую математику, необходимо выделить дополнительное время для подготовки.
Поскольку ОГЭ состоит из двух частей, первая из которых проверяет базовый уровень подготовки, а вторая включает более сложные задания, ребятам, изучающим в школе базовую математику, необходимо выделить дополнительное время для подготовки.
Иногда школьных уроков и самостоятельной работы достаточно, чтобы сдать ОГЭ на хорошо и отлично. В качестве подспорья можно использовать различные сайты и учебную литературу в открытом доступе. Возникающие вопросы можно обсудить на форумах или со школьным учителем. Но занятия на курсах помогают последовательно разобрать темы, систематизировать материал, проверить глубину его усвоения. Ведь после ОГЭ ребят через два года ждет более трудное испытание — ЕГЭ, в котором часть базовых заданий аналогичны заданиям повышенной и высокой сложности из ОГЭ. Девятиклассники впервые сдают экзамен, содержащий так много заданий, и его длительность составляет 3 часа 55 минут. Безусловно, для ребят это непросто.
Расскажите про структуру экзамена и систему начисления баллов. За какие задания на ОГЭ по математике ставится наибольшее количество баллов?
Всего школьникам предлагается 26 заданий. До недавнего времени экзамен состоял из трех частей — «Математика», «Реальная математика» и «Геометрия». С 2018 года раздела «Реальная математика» в ОГЭ больше нет, а его задания распределены между модулями «Алгебра» и «Геометрия».
Ребятам предстоит решить 17 задач по алгебре (14 задач в части 1 и три в части 2) и девять задач по геометрии (шесть задач в части 1 и три в части 2). Задания части 1 требуют краткого ответа в виде числа или последовательности цифр, которые вносятся в бланк ответов № 1. Развернутые решения заданий части 2 и ответы к ним записываются на бланке ответов № 2. За правильный ответ на каждое из заданий № 1-20 ставится 1 балл. Эти задания проверяются автоматически при сканировании бланков. Задания № 21-26 проверяют двое независимых экспертов, хотя при значительном расхождении оценок назначается проверка третьим экспертом. Эти задания могут быть оценены от 0 до 2 баллов. Таким образом, максимально за работу можно получить 32 первичных балла. Пятерка ставится за результат от 22 баллов, четверка — от 15 баллов, тройка — от 8 баллов (из них не менее 4 баллов по алгебре и 2 баллов по геометрии).
Эти задания могут быть оценены от 0 до 2 баллов. Таким образом, максимально за работу можно получить 32 первичных балла. Пятерка ставится за результат от 22 баллов, четверка — от 15 баллов, тройка — от 8 баллов (из них не менее 4 баллов по алгебре и 2 баллов по геометрии).
Как видите, для положительной оценки достаточно решить лишь восемь задач из части 1, а для пятерки — безошибочно выполнить базовую часть экзамена и только одно из заданий повышенной сложности. Вроде бы задача «сдать ОГЭ на отлично» не кажется такой уж сложной. Однако с заданиями повышенной сложности из части 2 ребятам придется снова столкнуться на ЕГЭ, уже в его базовой части. Например, задание № 22 повышенного уровня сложности — «текстовая задача» — аналогично заданию № 11 из части 1 ЕГЭ. Поэтому, как мне кажется, ребятам уже в 9 классе надо освоить методы и приемы решения заданий из части 2.
По вашему опыту преподавания, какие разделы математики самые сложные для школьников и вызывают наибольшее затруднение? Какие темы самые простые?
В модуле «Алгебра» это, прежде всего, исследование функций и построение их графиков. Задания на эту тему входят и в часть 1, и в часть 2 ОГЭ. В задании № 10 нужно установить соответствие между графиками функции и формулами, которые их задают. Здесь школьники часто ошибаются, пытаясь угадать ответ вместо того, чтобы рассуждать логически. В части 1 можно еще отметить задания на преобразование и вычисление выражений, если там содержатся радикалы: задание № 4, где надо найти значение выражения, и задание № 12, где сначала выражение надо упростить, а потом вычислить. Работать с корнями правильно получается далеко не у всех. Также не всегда ребятам удается справиться с заданием № 13 — «задачей прикладного содержания», где из несложной формулы нужно выразить одну из величин, найти ее значение, а ответ записать в указанных единицах измерения. Сложность здесь как раз заключается в переходе от одной размерности к другой.
В модуле «Геометрия» в части 1 включены задачи, относящиеся к ключевым разделам курса геометрии. И все же, если в задании встречаются такие темы, как «вписанная и описанная окружности», «вписанные углы», «соотношения между сторонами и углами прямоугольного треугольника», «подобие треугольников», показатель его решаемости падает.
И все же, если в задании встречаются такие темы, как «вписанная и описанная окружности», «вписанные углы», «соотношения между сторонами и углами прямоугольного треугольника», «подобие треугольников», показатель его решаемости падает.
Меньше всего ошибок девятиклассники допускают в заданиях на чтение таблиц и диаграмм, нахождение вероятности случайного события.
Какие есть «подводные камни» в заданиях части 2? На что нужно обратить внимание при подготовке к заданиям повышенной сложности?
| Задание № 21 | В этом задании необходимо решить уравнение или неравенство, преобразовать алгебраическое выражение. При решении рациональных и дробно-рациональных уравнений, а также уравнений высших степеней необходимо обращать внимание на возможность потери решения (при сокращении на выражение, которое может быть равным нулю) или получение посторонних решений (которые обнуляют знаменатель или обращают исходное уравнение в выражение, не имеющее смысла). При решении неравенств надо помнить, что при умножении неравенства на отрицательное выражение оно меняет знак. Зачастую школьники либо просто не обращают внимание на знак величины, на которую умножают неравенство, либо умножают неравенство на выражение, содержащее переменную. |
| Задание № 22 | Это текстовая задача, как правило, на «движение», «работу», «концентрации растворов» или «смеси и сплавы». Для ее решения необходимо составить уравнение или систему уравнений. Я бы посоветовала ребятам для наглядности обязательно заполнять таблицу, в которую вносятся известные по условию величины, выбранная переменная или переменные, после чего в пустые клетки вписываются соответствующие им величины, выраженные через введенные переменные, и только потом приступать к составлению уравнения (или системы). |
| Задание № 23 | Построение графика функции. Для правильного выполнения этого задания необходимо знать свойства следующих функций: линейная, квадратичная, либо функция, описывающая обратно пропорциональную зависимость. Также необходимо уметь строить графики этих функций, знать правила преобразования графиков. Очень часто встречаются задания, в которых формулу, задающую исходную функцию, можно преобразовать, после чего она значительно упрощается. Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать. Также необходимо уметь строить графики этих функций, знать правила преобразования графиков. Очень часто встречаются задания, в которых формулу, задающую исходную функцию, можно преобразовать, после чего она значительно упрощается. Здесь необходимо помнить, что область определения исходной и получившейся функции могут не совпадать. |
| Задание № 24 | Геометрическая задача вычислительного характера. Школьник должен решить планиметрическую задачу, применяя различные теоретические знания из курса геометрии. |
| Задание № 25 | Геометрическая задача на доказательство с использованием стандартных приемов. Здесь надо обратить внимание на умение математически грамотно и ясно записать решения, приведя все необходимые обоснования и пояснения. |
| Задание № 26 | Для решения этой задачи школьникам нужно владеть широким спектром приемов и способов рассуждений. Здесь возможно потребуются и дополнительные построения, и знание утверждений, не так часто используемых в школьном курсе. Например, теорема об угле между касательной и хордой; теорема о секущих и касательной; свойства высоты прямоугольного треугольника, опущенной из прямого угла; свойства биссектрис, медиан, высот треугольника; теорема Чевы; теорема Менелая. |
Что нужно делать школьнику, чтобы подготовиться к экзамену наилучшим образом? Как вы посоветуете им распределить свое время?
На занятиях со школьниками я обычно придерживаюсь следующей стратегии. Во-первых, мы полностью проходим программу 9 класса, начиная с отработки основных навыков и умений по следующим темам: преобразование алгебраических выражений, решение уравнений и неравенств, числовые последовательности, функции, их свойства и графики, элементы статистики и теории вероятностей. Постепенно повышая уровень заданий, мы переходим к решению задач повышенной и высокой сложности и стараемся уделить этим заданиям как можно больше внимания. Не менее трети времени следует посвятить геометрии, и здесь также нужно двигаться «от простого к сложному».
Не менее трети времени следует посвятить геометрии, и здесь также нужно двигаться «от простого к сложному».
Во-вторых, необходимо готовиться к самому формату ОГЭ, к его структуре. Если ученик хорошо умеет решать задачи, но ни разу не пробовал написать работу в этом формате, ему сложно будет оценить количество затрачиваемого времени на часть 1 и 2. Обязательно нужно научиться правильно распределять свои силы.
Многие девятиклассники не используют предлагаемое на экзамене время полностью, у них просто не хватает усидчивости. Ребята сдают работу раньше, хотя еще остались нерешенными задания повышенной сложности. Зачастую и в заданиях части 1 бывают ошибки по невнимательности, которые сам школьник не смог найти и исправить. На ЕГЭ же складывается обратная ситуация. Выпускники прилежно готовятся к экзамену, считают, что времени мало. Им хочется еще раз проверить свои решения и подумать над заданиями высокой сложности.
Какие источники вы рекомендуете использовать для самостоятельной подготовки к экзамену?
- «Сайт ФИПИ». На нем вы найдете открытый банк заданий ОГЭ.
- Сборник «ОГЭ. Математика 2018. Типовые и тестовые задания». Таких сборников очень много, нужно обращать внимание на гриф «рекомендовано ФИПИ».
- Учебные пособия Центра непрерывного математического образования. Например, сборник «Подготовка к ОГЭ по математике. Методические указания. Разбор задач». На 500 страницах здесь можно найти подробный разбор каждой из 26 задач экзамена и множество вариантов каждой из них для самостоятельного решения.
- «Сайт Alexlarin.net». Здесь каждую неделю выкладывается новый вариант ОГЭ и новый вариант ЕГЭ. Ребятам дается семь дней на размышление. Они могут обсуждать свои решения на специальном форуме. Потом вывешиваются правильные ответы.
- «РешуЕГЭ». На сайте доступен большой банк заданий. Тесты можно составлять самостоятельно, выбирая лишь те темы, над которыми необходимо поработать.
 Небольшой минус — тесты часто получаются похожими друг на друга.
Небольшой минус — тесты часто получаются похожими друг на друга.
Задачи на движение: скорость, время и расстояние.
Скорость – это физическая величина, показывающая какое расстояние пройдет объект за единицу времени.
Сегодня мы будем решать задачи на:
- движение
- скорость \(v=s/t\)
- время \(t=s/v\)
- расстояние \(s=v*t\)
Расстояние — путь, который нужно преодолеть во время движения.
Время — промежуток действия движения.
Скорость — характеристика движения.
Для решения задач необходимо ввести неизвестную, верно составить и решить уравнение.
Задача 1. Легковая машина прошла расстояние в \(160\) км за два часа. С какой скоростью двигалась машина?
Решение.
\(160/2=80\) км/час
Ответ: \(80.\)
Задача 2. Из города Минск в Смоленск, расстояние между которыми \(346\) км, отправились одновременно велосипедист и автомобилист. Скорость автомобиля \(20\) м/с, а велосипедиста \(20\) км/ч. Какое расстояние будет между ними через \(2\) часа?
Решение.
Мы не можем складывать разные единицы измерения, поэтому надо перевести м/с в км/ч. Как нам перевести км/ч в м/с? В км – 1000 м, в \(1\) ч \(-3600\), в \(1\) км/час\(-1000/3600\) м/c, то есть в \(1\) км/c \(-3600/1000\) м/c. \(20*\frac{3600}{1000}=72\). Итого скорость автомобиля \(72\) км/ч.
Так как автомобилист и велосипедист выехали из одного места и двигаются в одном направлении, расстояние между ними будет нарастать со скоростью:
- 72-20=52(км/ч)
- 52∗2=104 (км) – расстояние между ними через два часа.
Ответ: \(104\) км.
В таких задачах важно понимать:
- если мы умножаем скорость на время, то получаем расстояние;
- если расстояние делим на время, то получаем скорость;
- если расстояние делим на скорость, то получаем время ;
Задача 3. Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде. В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
Из А в В тронулись в одно время турист пешком, а второй турист – на велосипеде. В то же время из В в А выдвинулся мотоцикл, который встретился с велосипедистом через 3 часа, а с пешеходом через 4 часов после своего выезда из В. Найти расстояние от А до В, зная, что скорость пешехода 3 км/ч, а велосипедиста 10 км/ч.
10 * 3 = 30 (км) – мотоциклист от А через 3 часа.
3* 4 = 12 (км) – мотоциклист от А через 4 часов.
30 – 12 = 18 (км/ч) – скорость автомобиля.
10 + 18 = 28 (км/ч) – скорость сближения мотоциклиста и велосипедиста.
28 * 3 = 84 (км) – расстояние от А до В.
Ответ: 84 км.
Задача 4. Надувная лодка проплыла \(0,3\) км против течения реки, а затем проплыла еще \(3,9\) км по течению реки, затратив на это \(5\)часов и \(6\) минут. Найдите скорость лодки в стоячей воде, если скорость течения реки \(5\) км/ч.
Решение
Переведем \(5\) часов \(6\) минут в одинаковые единицы измерения, \(6\) мин — это \(\frac{1}{10}\) часа, итого \(5,1\) часа. Введем неизвестную х скорость в стоячей воде, \(x+5-\)скорость по течению, \(x-5-\)против течения реки.
Составляем уравнение:
- \(\frac{3,9}{x+5}+ \frac{0,3}{x-5}=5,1\)
- \(3,9x-19,5+0,3x+1,5=5,1\)
- \(4,2x-18=5,1\)
- \(4,2x=23,1\)
- \(x=5,5 \) км/ч – скорость в стоячей воде.
Ответ: \(5,5\) км/ч.
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
6 характеристик сложных математических задач
Разнообразные математические задачи необходимы для привлечения учащихся и создания динамичных классов. В этом посте, адаптированном из ее книги Моделирование с математикой , Нэнси Батлер Вольф рассматривает шесть характеристик, присущих лучшим математическим задачам.
В этом посте, адаптированном из ее книги Моделирование с математикой , Нэнси Батлер Вольф рассматривает шесть характеристик, присущих лучшим математическим задачам.
Как отличить хорошее задание от плохого? По мере того, как учителя делают набег на математическое моделирование в своих классах, важно, чтобы они использовали сложные и полезные задания.К сожалению, слишком мало учебников содержат такие задания, поэтому учителям приходится изо всех сил пытаться найти или разработать свои собственные. Вот краткий обзор шести важных характеристик сложных задач моделирования:
- Доступность для всех учащихся Первая характеристика должна быть очевидна почти любому учителю практически в любом классе: ученики за партами перед нами обладают широким спектром базовых знаний, математическим образованием и опытом работы с математикой.Если задача действительно сложная, она вызовет интерес, мотивацию и вызов для всех наших учеников. Это не будет способствовать тому, чтобы наши студенты, находящиеся в наиболее затруднительном положении, отказывались от участия, и не позволит более опытным студентам взять на себя руководство, дать направление и предложить решения. Точно так же более продвинутые студенты-математики не смогут быстро и легко решить эту задачу, но и для этих учащихся возникнут проблемы и дополнения. Хорошее задание предоставит всем учащимся возможность внести свой вклад с уверенностью.
- Реальные задачи
Второй критерий для сложной задачи уже много лет является предметом обширных дискуссий среди учителей, математиков и исследователей. Что именно представляет собой задача, имеющая какую-то основу в реальной жизни? Но остается вопрос: что такое настоящая задача? Я бы предположил, что подлинное задание — это задание, с которым студенты имеют некоторый реальный жизненный опыт. Я использовал множество задач по решению проблем и моделированию, которые, по общему признанию, «не совсем реальны», но, тем не менее, интересны и увлекательны для студентов. Например, математика, имеющая связь с литературой, может быть очень интересной и увлекательной для учащихся, несмотря на то, что исследуемые сценарии нельзя назвать «действительно реальными». Помните, что цель состоит в том, чтобы представить задания, которые интересны и могут помочь учащимся понять, что концепции, которые они изучают в своих классах математики, не полностью отделены от их жизни вне класса. Не подавляйте свое творчество, налагая ложные ограничения на то, что является «реальным» приложением.Студенты будут вовлечены в проблемы, которые возникают из литературы, из других предметных областей и из их воображения, а также из их «действительно реальной» жизни!
Например, математика, имеющая связь с литературой, может быть очень интересной и увлекательной для учащихся, несмотря на то, что исследуемые сценарии нельзя назвать «действительно реальными». Помните, что цель состоит в том, чтобы представить задания, которые интересны и могут помочь учащимся понять, что концепции, которые они изучают в своих классах математики, не полностью отделены от их жизни вне класса. Не подавляйте свое творчество, налагая ложные ограничения на то, что является «реальным» приложением.Студенты будут вовлечены в проблемы, которые возникают из литературы, из других предметных областей и из их воображения, а также из их «действительно реальной» жизни! - Множественные подходы и представление Третий критерий сложной математической задачи — то, что она поддается разнообразию подходов и представлений. Наши ученики подходят к математике с самых разных точек зрения, и когда мы сможем признать и уважать этот факт, мы сможем предоставить больше возможностей для успеха учеников.Когда различные подходы могут привести к подходящему решению, учащиеся могут стать уверенными в своих силах и учиться друг у друга.
- Сотрудничество и обсуждение Четвертая характеристика сложной задачи моделирования заключается в том, что она поощряет сотрудничество и обсуждение. Стратегии обучения моделированию задач различаются, но в каждом случае они должны предполагать определенную степень сотрудничества и обсуждения. Многие задачи требуют, чтобы учащиеся сначала работали самостоятельно, при необходимости под руководством и поддержкой учителя.Когда учащиеся пришли к независимому выводу, они могут поделиться своими результатами, подходами и представлениями в рамках совместных групп и обсудить сходства и различия. Учащиеся получают новые идеи и перспективы, услышав мнение своих сверстников; даже учащиеся, испытывающие трудности, начинают обретать уверенность в своей способности решать проблемы, когда им предоставляется возможность объяснить свои рассуждения по проблеме.

- Вовлеченность, любопытство и творчество Следующие характеристики сложной задачи не требуют пояснений и идут рука об руку друг с другом, а также с другими характеристиками.Когда задача интересна и увлекательна и ставит задачу, которая интересует учащихся, они будут настойчиво решать ее. Богатая задача представляет учащимся множество возможных подходов и представлений, предоставляя доступ всем учащимся. Когда учащиеся решают проблему, они должны сначала решить, какие инструменты и какой подход попробовать. По мере развития проблемы учащиеся могут столкнуться с препятствиями и препятствиями, которые потребуют от них принятия большего количества решений как индивидуально, так и совместно, и, зачастую, потребуют творческого подхода и разнообразия в способах применения своих знаний.
- Возможности расширения Последняя характеристика сложной задачи моделирования часто является недостающей частью опыта решения проблем в классе. Мы, вероятно, все можем относиться к случаям, когда мы предлагали студентам увлекательное задание, только чтобы обнаружить, что одна группа быстро заканчивает, в то время как другая группа борется с проблемой. Это может привести к одному из двух сценариев: безумная попытка удержать более продвинутую группу занятой (или тихой), пока другая группа продолжает свою работу, или попытка поспешить с более медленной группой, чтобы все не отвлекались.Богатая задача удерживает всех учащихся вовлеченными, включая задачи и расширения для более продвинутых учеников, в то время как другие ученики продолжают работать, не заставляя «поторопиться и закончить».
Существует множество источников для сложных математических задач, включая задачи MARS, математические задачи с 3 актами и задачи освещения. По мере того, как вы будете работать с подобными проблемами, вам станет легче распознать хорошую задачу математического моделирования и развить собственный богатый математический опыт для ваших учеников, и вы начнете видеть окупаемость ваших вложений времени и энергии в энтузиазм и мотивацию. , и глубина понимания ваших учеников.
, и глубина понимания ваших учеников.
Хотите узнать больше о том, как начать или углубиться в математическое моделирование? Посмотрите, как Нэнси рассказывает о том, почему моделирование так эффективно, или просмотрите первую главу Моделирование с помощью математики .
♦ ♦ ♦ ♦
Нэнси Батлер Вольф — национальный консультант по математике и разработчик учебных программ, входившая в состав группы написания иллюминаций NCTM. Она имеет более 30 лет опыта преподавания в классе и выступала на различных конференциях по математическому моделированию и алгебраическим рассуждениям.Следуйте за ней в Twitter @drnanbut.
Математическая задача — обзор
Общая дискуссия: основные выводы и новые вопросы
Тревога по поводу математики — широко распространенное явление, которое, по оценкам, затрагивает примерно каждого пятого человека при выполнении числовых и математических задач как в школе, так и в дневное время сегодняшняя жизнь (Ashcraft et al., 2007). К настоящему времени исследования позволили выявить значительный объем последствий математической тревожности, хотя на маленьких детях ее начали изучать только недавно.По мере того, как все больше и больше исследований показывают появление математической тревожности в раннем детстве, все больший упор делается на раскрытие ее истоков или корней развития: почему одни дети становятся озабоченными математикой, а другие нет?
Несмотря на небольшое количество эмпирических исследований, было много анекдотических предположений о причинах математической тревожности, часто подчеркивающих влияние окружающей среды, например родителей и учителей. В данной главе мы специально сосредоточились на возможной роли родителей.Прежде чем приступить к рассмотрению эмпирических данных о взаимосвязи между тревожностью родителей и детей, связанной с математикой, мы использовали исследования из общей литературы о детской тревоге. Мы пришли к выводу, что есть некоторые свидетельства в пользу процессов моделирования родительских ролей: математическая тревога родителей связана с математической тревогой у детей, но эта взаимосвязь может регулироваться полом и участием родителей.
Это вызывает несколько интересных вопросов. Во-первых, почему мы видим эти гендерные эффекты? Это потому, что родители больше занимаются математикой со своими сыновьями? Или это результат того, как девочки отвечают на вопросы анкеты по математике? Дальнейшие исследования с использованием домашней оценки математической грамотности и различных показателей математической тревожности помогут нам проанализировать эти возможности.Во-вторых, важно спросить, как мы можем решить проблему передачи математической тревожности от родителей к ребенку. Существуют ли какие-либо конкретные меры, которые могут помочь родителям уменьшить передачу их беспокойства по поводу математики? Например, следует ли побуждать озабоченных математикой родителей меньше заниматься математикой со своими детьми? Могут ли другие взрослые образцы для подражания (например, учителя), которые не озабочены математикой, служить буфером против озабоченных математикой родителей? Вероятно, что многие факторы окружающей среды взаимодействуют друг с другом, но, насколько нам известно, в исследованиях эти взаимодействия еще не рассматривались.Что произойдет, если у ребенка будут родители, озабоченные математикой, и учитель, озабоченный математикой? Их результаты мультипликативно хуже? Наконец, как влияние окружающей среды взаимодействует с личными факторами (например, неуверенностью) и когнитивными аспектами (например, плохой рабочей памятью)?
В целом, есть некоторые свидетельства в поддержку анекдотических предположений о том, что родители играют роль в формировании отношения и беспокойства своих детей по отношению к математике. Эти предложения согласуются с общей литературой по тревоге, которая определяет родителей как ключевой фактор риска.В этом общем исследовании тревожности исследования демонстрируют ряд родительских влияний, включая стили воспитания, отношения привязанности, ролевое моделирование, передачу информации и подкрепление. Не исключено, что эти результаты также могут быть применены к математике в области тревожности. В самом деле, может быть полезно продолжить это исследование, поскольку мы пытаемся раскрыть корни развития детской математической тревожности.
В самом деле, может быть полезно продолжить это исследование, поскольку мы пытаемся раскрыть корни развития детской математической тревожности.
Знания по математическому заданию для обучения | SpringerLink
Статьи этого номера журнала «Педагог математики» [JMTE] побудили меня задуматься о математических задачах и знаниях учителей о них.Математические задачи занимают центральное место в изучении математики. Например, они могут «дать учащимся стимул задуматься над конкретными концепциями и процедурами, их связями с другими математическими идеями и их применением в реальных условиях» (Национальный совет учителей математики [NCTM] 1991, стр. 24 ). Однако у них нет собственной жизни как инструмента для обучения. Именно учитель и ученики дают им жизнь в зависимости от того, как они интерпретируются и разыгрываются в классе.Учитель играет решающую роль в формировании жизненной задачи и руководстве деятельностью учащихся, чтобы через них у учащихся была возможность осмысленно заниматься математикой. Учитель мог превратить открытое задание в закрытое или закрытое в открытое. Он или она может относиться к задаче с высоким когнитивным спросом как к задаче низкого уровня или наоборот. На это может повлиять несколько факторов; например, знание преподавателем содержания, знания учащихся, цель задания, учебная ориентация и убеждения относительно математики.В частности, характер знаний учителей о математических задачах для обучения, вероятно, будет определяющим фактором в их подходе к задачам.
Знания математических задач для преподавания связаны с знаниями, необходимыми учителям для (а) выбора и разработки задач, способствующих концептуальному пониманию математики учащимися, поддержки их развития математического мышления и захвата их интереса и любопытства и (б) оптимизировать обучающий потенциал таких задач. Эти знания включают следующее:
Эти знания включают следующее:
- 1.
Понимание природы стоящих задач — например, значительного математического содержания; можно решить несколькими способами; использовать несколько представлений; подключиться к другим важным математическим идеям; требовать от студентов обоснования, интерпретации, предположений; имеют высокий когнитивный спрос (например, NCTM 1991, 2010; Stein et al. 2000).
- 2.
Способность определять, выбирать и создавать задачи, богатые математически с точки зрения содержания, педагогически с точки зрения обеспечения осмысленного и глубокого понимания математики, а также лично для учащихся с точки зрения их интересов и потребностей в обучении.
- 3.
Знание уровней когнитивных требований к задачам (например, Stein et al. 2000) и отношения к целям задачи с точки зрения уровня обучения и понимания математики, которые они могут продвигать.
- 4.
Знание понимания, интересов и опыта учащихся, а также диапазона способов, которыми разные учащиеся изучают математику (NCTM1991, стр.25).
- 5.
Понимание того, как учителя выбирают задания и как они их используют, влияет на то, как учащиеся приходят к пониманию математики, а также к выполнению и применению математики.
- 6.
Знание
, какие аспекты задачи выделить, как организовать и организовать работу студентов, какие вопросы задать, чтобы бросить вызов тем, у кого разный уровень знаний, и как поддержать студентов, не принимая на себя процесс мышления за них и, таким образом, устраняя соревнование.
(NCTM 2000, стр. 19).
Знания математических задач для обучения, таким образом, многомерны, и поэтому учителю, вероятно, будет сложно построить без значимого вмешательства, основанного на его или его первоначальном осмыслении задач. В моем опыте работы с учителями математики в старших классах я столкнулся с целым рядом подходов к выбору задач. Например, были учителя, которые задавали задачи с четными (или нечетными) числами, потому что ответы на них были в конце учебника.Были и те, кто намеренно пропускал задачи, требующие неалгоритмического мышления. Были те, кто минимизировал использование словесных задач или максимизировал использование тех, контекст которых соответствовал интересам учащихся. Были те, кто считал исследовательские задания на уровне старшей школы пустой тратой времени и практически не влиял на успеваемость учащихся по математике. В этих действиях или мышлении воплощены убеждения в отношении задач, которые создают препятствия для изучения учащимися математики и усвоения учителями стоящих задач.Такие убеждения усложняют задачу помочь учителям развить значимые знания математических задач для обучения. Пример этого отражен в исследовании Carson (2010), магистерской диссертации, которую я руководил.
Карсон исследовал убеждения учителей математики в старших классах (9–12 классы) относительно исследовательских математических задач при изучении и преподавании математики в старших классах. Пятеро учителей, которые вызвались участвовать в исследовании, были участниками однодневного семинара «Исследовательская учебная деятельность» (ELA), который спонсировался их школьной системой и был открыт для всех учителей математики в средней школе.Они не использовали исследовательские задания в своем обучении, но были заинтересованы в их изучении, учитывая, что в ближайшее время будут реализованы акценты на исследованиях в учебной программе. Карсон вела семинар в качестве консультанта по математике в школьной системе. Семь ELA, использованных на семинаре, предоставили различные примеры исследовательских задач, были непосредственно применимы к темам в учебной программе и могли быть адаптированы к различным классам. Они включали: доказательства шаблонов чисел; исследование закономерностей в треугольнике Паскаля; исследование обратных функций; исследование свойств полиномиальных функций; использование мысленных образов и пространственной памяти для распознавания и воспроизведения геометрических фигур; изучение математики в историях женского математика; и сложение и умножение радикалов посредством визуального представления.Учителя работали над заданием в группах. В конце каждого задания каждый учитель заполнял лист для размышлений с подсказками, которые включали: Что такое математика? Что мы хотим, чтобы студенты заметили? Какова роль учителя? Затем последовало обсуждение и обсуждение в классе.
Семь ELA, использованных на семинаре, предоставили различные примеры исследовательских задач, были непосредственно применимы к темам в учебной программе и могли быть адаптированы к различным классам. Они включали: доказательства шаблонов чисел; исследование закономерностей в треугольнике Паскаля; исследование обратных функций; исследование свойств полиномиальных функций; использование мысленных образов и пространственной памяти для распознавания и воспроизведения геометрических фигур; изучение математики в историях женского математика; и сложение и умножение радикалов посредством визуального представления.Учителя работали над заданием в группах. В конце каждого задания каждый учитель заполнял лист для размышлений с подсказками, которые включали: Что такое математика? Что мы хотим, чтобы студенты заметили? Какова роль учителя? Затем последовало обсуждение и обсуждение в классе.
Один из аспектов результатов был сосредоточен на том, как пять участников думали о ELA после семинара. Интерпретация ELA этими учителями была связана с тем, как они рассматривали участие учеников в их работе и чего они позволяли ученикам достигать в учебе.Основываясь на их убеждениях в отношении ELA во время индивидуальных собеседований после семинара, были определены четыре взаимосвязанные темы, касающиеся их убеждений в отношении ELA: ELA ориентированы на учащихся (например, позволяют учащимся изучать математику посредством открытий вместо того, чтобы им рассказывать о концепциях, является ли учащимся направлен и допускает совместную работу). ELA может улучшить понимание учащимися математики. ELA может повысить вовлеченность учащихся в изучение математики (например, за счет повышения интереса и удовольствия).ELA может предоставить студентам практический и / или исследовательский опыт.
Несмотря на эти способы просмотра ELA, учителя не изменили своих взглядов на ELA в своей практике. Они рассматривали их как отдельные события в своей практике. Карсон объяснил: «Размышления учителей показали, что текущее и предполагаемое использование ELA должно было происходить в отдельных местах их практики. Похоже, они не перенесли свои взгляды на ELA на то, «как» это может стать доминирующей педагогикой »(стр.149). Хотя задачи, использованные на семинаре, не были масштабными проектами, учителя по-прежнему рассматривали ELA как «тщательно продуманные пакеты», которые требуют много времени на разработку и требуют больше времени на планирование, чем это доступно в рамках их рабочих параметров и среды. Как объяснил один учитель: «Вы действительно должны быть готовы уделять много времени вне школы, потому что вы не собираетесь делать это в школе» (с.150). Они также указали, что не было единого доступного ресурса, который предоставлял бы все ELA, применимые к учебной программе, оправдывая необходимость их создания или поиска.Карсон пришел к выводу, что «существуют ограничительные убеждения, мешающие учителям включать ELA в повседневную практику» (стр. 149). «У них нет глубокого понимания природы ELA, чтобы можно было легко трансформировать практику» (стр. 150). Таким образом, хотя однодневный семинар позволил учителям понять ELA как значимые педагогические инструменты, неудивительно, что им было недостаточно выработать значимые знания задач для обучения в общем виде и противостоять убеждениям, которых они придерживались. оправдано ограничение или отказ от использования ELA в их обучении.Фактически, семинар мог непреднамеренно укрепить их «основные убеждения» (Green, 1971), которые ограничивают объем задач и то, как они вовлекают учащихся в их выполнение в своих классах. Таким образом, помимо других ограничений этой формы вмешательства, явное следование убеждениям должно быть важным фактором, помогающим учителям преобразовать свое мышление и обучение с помощью ELA.
Похоже, они не перенесли свои взгляды на ELA на то, «как» это может стать доминирующей педагогикой »(стр.149). Хотя задачи, использованные на семинаре, не были масштабными проектами, учителя по-прежнему рассматривали ELA как «тщательно продуманные пакеты», которые требуют много времени на разработку и требуют больше времени на планирование, чем это доступно в рамках их рабочих параметров и среды. Как объяснил один учитель: «Вы действительно должны быть готовы уделять много времени вне школы, потому что вы не собираетесь делать это в школе» (с.150). Они также указали, что не было единого доступного ресурса, который предоставлял бы все ELA, применимые к учебной программе, оправдывая необходимость их создания или поиска.Карсон пришел к выводу, что «существуют ограничительные убеждения, мешающие учителям включать ELA в повседневную практику» (стр. 149). «У них нет глубокого понимания природы ELA, чтобы можно было легко трансформировать практику» (стр. 150). Таким образом, хотя однодневный семинар позволил учителям понять ELA как значимые педагогические инструменты, неудивительно, что им было недостаточно выработать значимые знания задач для обучения в общем виде и противостоять убеждениям, которых они придерживались. оправдано ограничение или отказ от использования ELA в их обучении.Фактически, семинар мог непреднамеренно укрепить их «основные убеждения» (Green, 1971), которые ограничивают объем задач и то, как они вовлекают учащихся в их выполнение в своих классах. Таким образом, помимо других ограничений этой формы вмешательства, явное следование убеждениям должно быть важным фактором, помогающим учителям преобразовать свое мышление и обучение с помощью ELA.
В общем, привлечения учителей к выполнению стоящих задач может быть недостаточно для их развития знаний по математическим задачам для преподавания, как определено ранее.Такое участие может помочь им понять отдельный аспект этих знаний, но не все компоненты, которые необходимы для полноценной реализации. Как может выглядеть подходящее вмешательство, учитывающее убеждения, требует постоянных исследований с явным акцентом на знание математических задач для обучения. Однако, как показывают исследования в этой области, задания действительно играют ключевую роль в обучении учителей математики. Они обеспечивают значимое вмешательство для повышения уровня знаний и практических навыков учителей.Статьи в этом выпуске JMTE дополнительно подчеркивают важность задач в обучении учителей.
Однако, как показывают исследования в этой области, задания действительно играют ключевую роль в обучении учителей математики. Они обеспечивают значимое вмешательство для повышения уровня знаний и практических навыков учителей.Статьи в этом выпуске JMTE дополнительно подчеркивают важность задач в обучении учителей.
В статье Мелиссы Браун подробно рассматриваются аспекты знания математических задач для обучения, уделяя особое внимание пониманию учителями выбора и выполнения когнитивно сложных математических задач. Как она объясняет, для улучшения возможностей учащихся изучать математику с пониманием требуется, чтобы учителя математики выбирали и выполняли задачи высокого уровня таким образом, чтобы поддерживать участие учащихся в мышлении и рассуждениях на протяжении всего учебного эпизода.Статья Раисы Губерман и Розы Лейкин косвенно затрагивает аспекты знания математических задач для обучения, привлекая будущих учителей к решению задач с несколькими решениями. Хотя их внимание сосредоточено на развитии навыков решения проблем, опыт решения этих задач, вероятно, позволил бы будущим учителям осознать природу и значимость таких задач в их обучении. Однако аспект работы, в котором предполагаемые учителя участвовали в оценке уровня интереса и уровня сложности математических задач, более непосредственно связан со знанием задач для обучения.В статье Тони Гау Бартелл, Кори Уэбел, Брайана Боуэна и Нэнси Дайсон речь идет о будущих учителях, которые учатся различать доказательства концептуального понимания и процедурных знаний, а также особенности, свидетельствующие о концептуальном понимании, и те, которые этого не делают. Хотя это явно не касается задач, доказательства основаны на решениях задач учащимися. Природа таких задач и их отношение к концептуальным и процедурным знаниям имеют значение для знаний задач для обучения.В целом, эти три статьи предлагают содержательные примеры различных вмешательств, чтобы облегчить учителям усвоение заданий и другие способы придать смысл преподаванию математики для более глубокого понимания.
Мелисса Бостон исследовала меры по улучшению преподавания математики в направлении идеалов NCTM. Проект «Повышение уровня подготовки учителей средней математики» (ESP) предоставил учителям средней математики опыт профессионального обучения, ориентированный на выбор и выполнение интеллектуально сложных математических задач.Центральная последовательность действий на семинаре заключалась в том, чтобы привлечь учителей к решению когнитивно сложной математической задачи, проанализировать когнитивные требования задачи и поразмышлять над учебными артефактами (например, работой учащихся) или учебным эпизодом (например, повествованием или видео). кейсы) учителя, использующего задачу на уроке математики. Бостон исследовал связь между опытом учителей в проекте ESP, изменениями в знаниях учителей и наблюдаемыми изменениями в практике преподавания учителей.В частности, она рассмотрела способы, которыми знания учителей о когнитивных требованиях математических задач изменились после их участия в семинаре по профессиональному развитию ESP, и взаимосвязь между изменениями в знаниях учителей познавательных требований математических задач и их опытом обучения семинар по профессиональному развитию ESP.
Результаты исследования показали, что в конце семинара учителя ESP значительно расширили свои знания о когнитивных потребностях математических задач и обладали значительно более высокими знаниями, чем учителя в контрастной группе.Учителя ESP развили новые идеи о влиянии математических задач на обучение студентов. Появились свидетельства того, что они стали лучше понимать, как задания высокого уровня способствуют учебе учащихся. Однако они часто упускают из виду лежащие в основе математические концепции или связи, встроенные в задачи высокого уровня. В процедурах с задачами связи половина учителей ESP настаивала на определении наличия процедуры как признака, определяющего уровень когнитивных требований («процедуры = низкий уровень»).Небольшая группа учителей сосредоточилась на тех чертах задачи, которые казались «отсутствующими», такими как реальный контекст или подсказка для объяснения, и, по-видимому, рассматривали и то, и другое как необходимые условия для выполнения требований высокого уровня. Однако учителя больше не оценивали уровень спроса на основе предполагаемой сложности математического содержания или навыков. Произошли изменения в их ориентации на свои учебные планы (реформированные или традиционные), которые способствовали выбору учебных заданий высокого уровня в их собственных классах.В целом, исследование представляет собой пример того, как вмешательство, предполагающее понимание уровней когнитивных требований задач, может помочь учителям улучшить свои знания и учебную практику по тем аспектам обучения, которые были связаны с расширением возможностей учащихся для обучения. Он также дает представление о многообещающем подходе, который поможет учителям развить знания по математическим задачам для обучения.
Однако учителя больше не оценивали уровень спроса на основе предполагаемой сложности математического содержания или навыков. Произошли изменения в их ориентации на свои учебные планы (реформированные или традиционные), которые способствовали выбору учебных заданий высокого уровня в их собственных классах.В целом, исследование представляет собой пример того, как вмешательство, предполагающее понимание уровней когнитивных требований задач, может помочь учителям улучшить свои знания и учебную практику по тем аспектам обучения, которые были связаны с расширением возможностей учащихся для обучения. Он также дает представление о многообещающем подходе, который поможет учителям развить знания по математическим задачам для обучения.
Раиса Губерман и Роза Лейкин изучали развитие способностей учителей решать проблемы посредством использования задач с несколькими решениями и изменения их взглядов на уровни интереса и сложности задач в курсе решения проблем для будущей начальной школы. учителя математики.Авторы рассматривают задачи с несколькими решениями как задачи, содержащие явное требование для решения проблемы несколькими способами. Различия и сходство между решениями можно проиллюстрировать с помощью: (а) различных представлений математической концепции, (б) различных свойств (определений или теорем) математических концепций из определенной математической темы, или (в) различных математических инструментов и теоремы из разных разделов математики.
Анализ данных включал определение стратегий участников, используемых при решении задач элементарной математики с несколькими решениями, и их способности находить несколько решений проблем, а также определение их оценок уровня интереса и уровня сложности решаемых ими проблем.Ключевой вывод исследования показал, что задачи с несколькими решениями были эффективны, помогая как участникам, которые были хорошо успевающими по математике, так и тем, кто был неуспевающим, значительно улучшить свои навыки решения проблем. Однако отличники улучшили свои достижения более заметно, чем люди с низкими показателями. Другой ключевой вывод заключался в значительном сдвиге в стратегиях решения проблем участников для задач с несколькими решениями от в основном стратегий проб и ошибок, используемых в предварительном тесте, к систематическим стратегиям в пост-тесте.К концу курса участники гибко решали проблемы, меняли используемые представления и применяли более продвинутые стратегии решения проблем.
Однако отличники улучшили свои достижения более заметно, чем люди с низкими показателями. Другой ключевой вывод заключался в значительном сдвиге в стратегиях решения проблем участников для задач с несколькими решениями от в основном стратегий проб и ошибок, используемых в предварительном тесте, к систематическим стратегиям в пост-тесте.К концу курса участники гибко решали проблемы, меняли используемые представления и применяли более продвинутые стратегии решения проблем.
Наконец, что касается мнений участников об уровне интереса и сложности заданий, результаты показали, что они незначительно изменились как в систематическом (через обсуждение всей группы со сверстниками), так и в ремесленном режиме (путем интервьюирования школьников. ). Систематический и ремесленный опыт оказал противоположное влияние (в большинстве случаев) на мнение участников об интересе и сложности проблем.Например, после обсуждения участники с высокими показателями оценили сложность задач ниже, чем до обсуждения, но после интервью они повысили свои баллы. Корреляция между оценкой участниками сложности проблемы и интересом к проблеме оказалась значимой после решения задач в ходе предварительного тестирования и еще более значимой после опроса школьников. В целом, исследование представляет собой пример того, как вмешательство, включающее несколько задач, может помочь будущим учителям улучшить свои знания в области решения проблем.Он также дает представление о взаимосвязи между их оценкой уровня сложности и уровнем интереса к задачам, которые имеют значение для помощи учителям в развитии знаний по математическим задачам для обучения.
Тоня Гау Бартелл, Кори Вебел, Брайан Боуэн и Нэнси Дайсон изучали роль, которую знание содержания играет в способности будущих учителей распознавать свидетельства концептуального понимания детьми математики, и влияние вмешательства, направленного на поддержку их в распознавании свидетельств детского концептуальное понимание математики.Вмешательство было разработано таким образом, чтобы включать примеры, в которых дети использовали правильные процедуры и в которые они включали нерелевантные доказательства, которые можно было принять за доказательства понимания. Это было частью курса, который был направлен на развитие математического понимания будущих учителей ключевых числовых и операционных тем, которые обычно разрабатываются с детьми младших классов. Результаты были сосредоточены на трех областях содержания: сравнение и умножение дробей и вычитание десятичных знаков. Анализ знаний участников об этих концепциях показал, что все участники продемонстрировали некоторые доказательства концептуального понимания вычитания десятичных знаков, большинство продемонстрировали некоторые доказательства концептуального понимания сравнения дробей, но лишь немногие продемонстрировали доказательства концептуального понимания умножение дробей.Независимо от знания содержания, до вмешательства во все три области содержания, большинство участников распознавали ответы детей, демонстрирующие концептуальное понимание как таковое, и наиболее охарактеризованные процедурные реакции детей как свидетельство концептуального понимания. Кроме того, знание содержания, по-видимому, поддерживало анализ ответов участников с концептуальными характеристиками только для сравнения содержания фракций. Для сравнения дробей знание содержания помогло участникам распознать доказательства концептуального понимания детей, но не помогло умножению дробей.
Это было частью курса, который был направлен на развитие математического понимания будущих учителей ключевых числовых и операционных тем, которые обычно разрабатываются с детьми младших классов. Результаты были сосредоточены на трех областях содержания: сравнение и умножение дробей и вычитание десятичных знаков. Анализ знаний участников об этих концепциях показал, что все участники продемонстрировали некоторые доказательства концептуального понимания вычитания десятичных знаков, большинство продемонстрировали некоторые доказательства концептуального понимания сравнения дробей, но лишь немногие продемонстрировали доказательства концептуального понимания умножение дробей.Независимо от знания содержания, до вмешательства во все три области содержания, большинство участников распознавали ответы детей, демонстрирующие концептуальное понимание как таковое, и наиболее охарактеризованные процедурные реакции детей как свидетельство концептуального понимания. Кроме того, знание содержания, по-видимому, поддерживало анализ ответов участников с концептуальными характеристиками только для сравнения содержания фракций. Для сравнения дробей знание содержания помогло участникам распознать доказательства концептуального понимания детей, но не помогло умножению дробей.
Вмешательство было успешным в отвлечении участников от оценки ответов с концептуальными особенностями и процедурными решениями в качестве доказательства концептуального понимания для вычитания содержания десятичных знаков. Хотя некоторые участники также отошли от оценки таких ответов как свидетельства концептуального понимания умножения содержания фракций, многие по-прежнему рассматривали эти ответы как свидетельство концептуального понимания после вмешательства. Это также верно для анализа процедурных ответов при сравнении содержания фракций.Кроме того, в тех областях, где наблюдался рост анализа участниками математической работы детей, участники также имели тенденцию критиковать ответы детей, предполагая, что ответы с концептуальными особенностями или процедурными решениями были свидетельством того, что ребенок не понимал математику. Авторы пришли к выводу, что содержательные знания необходимы, но недостаточны для поддержки способности будущих учителей распознавать доказательства концептуального понимания детьми математики.Хотя вмешательство действительно оказалось значительным, тот факт, что даже после вмешательства многие участники рассматривали процедурные ответы или те, которые содержат концептуальные особенности, как свидетельство концептуального понимания, указывает на возможность дальнейшего развития.
Авторы пришли к выводу, что содержательные знания необходимы, но недостаточны для поддержки способности будущих учителей распознавать доказательства концептуального понимания детьми математики.Хотя вмешательство действительно оказалось значительным, тот факт, что даже после вмешательства многие участники рассматривали процедурные ответы или те, которые содержат концептуальные особенности, как свидетельство концептуального понимания, указывает на возможность дальнейшего развития.
В этих трех статьях рассказывается о значимых мероприятиях и возможных проблемах, которые помогут учителям улучшить свои знания для преподавания математики. Они имеют значение для педагогического образования в связи со знанием математических задач для обучения.Например, все вместе они демонстрируют важность вовлечения учителей не только в решение стоящих задач. Они предполагают, что учителя могут также анализировать когнитивные требования задачи, размышлять над учебными артефактами (например, работой учеников) или учебным эпизодом (например, повествованием или видеоматериалами) учителя, использующего задачу на уроке математики, анализировать проблемы с точки зрения уровня интереса и сложности, участвовать в групповом обсуждении множества решений со сверстниками, проводить собеседование со школьниками о задачах и находить доказательства концептуального понимания детей в их решениях задач.Тем не менее, необходимы постоянные исследования, чтобы определить природу знаний о математических задачах для преподавания в связи с практикой и другими эффективными способами помощи учителям в их развитии.
Ссылки
Карсон, Р. (2010). Мнение учителя математики средней школы в отношении исследовательской учебной деятельности . Неопубликованная магистерская диссертация, Университет Калгари.
Зеленая, Т.(1971). Педагогическая деятельность . Нью-Йорк: Макгроу-Хилл.
Google ученый
http://www.
 nctm.org/uploadedFiles/Research_News_and_Advocacy/Research/Clips_and_Briefs/Research_brief_14_-_Problem_Solving.pdf. Загружено 30 декабря 2012 г.
nctm.org/uploadedFiles/Research_News_and_Advocacy/Research/Clips_and_Briefs/Research_brief_14_-_Problem_Solving.pdf. Загружено 30 декабря 2012 г.Национальный совет учителей математики. (1991). Профессиональные стандарты обучения математике . Рестон, Вирджиния: Национальный совет учителей математики.
Google ученый
Национальный совет учителей математики. (2000). Принципы и стандарты школьной математики . Рестон, Вирджиния: Национальный совет учителей математики.
Google ученый
Национальный совет учителей математики (апрель 2010 г.). Краткое исследование: Решение проблем.
Штейн, М.К., Смит, М.С., Хеннингсен, М., и Сильвер, Е.А. (2000). Внедрение основанного на стандартах обучения математике: справочник по профессиональному развитию . Нью-Йорк: издательство Teachers College Press.
Google ученый
Скачать ссылки
Информация об авторе
Принадлежность
Факультет образования, Университет Калгари, 2500 University Drive NW, Calgary, AB, T2N1N4, Canada
Olive Chapman
Для корреспонденции автора
к Олив Чепмен.
Об этой статье
Цитируйте эту статью
Чепмен О. Знание математических задач для обучения. J Math Teacher Educ 16, 1–6 (2013). https://doi.org/10.1007/s10857-013-9234-7
Скачать цитату
Rich Mathematical Tasks
Ваш браузер не поддерживает джаваскрипт! Этот сайт использует JavaScript, но полностью работает без него. МатематикаСодержание страницы
Введение
Богатые математические задачи помогают учащимся осмыслить их через более глубокое обучение, которое требует высокого уровня мышления, рассуждений и решения проблем. Комитет VDOE Rich Mathematical Task Committee, состоящий из руководителей учителей математики со всего Содружества, создал математически насыщенные задачи, соответствующие Стандартам обучения по математике от 2016 года . Комитет создал шаблоны реализации задач до того, как приступить к их администрированию в классах. Для многих задач комитет оценивал задачи индивидуально, откалибровал их оценку с командой, предоставил обоснование выставления оценок и отобрал студенческие работы, которые будут служить в качестве якорных документов.Департамент образования Вирджинии хотел бы выразить особую благодарность Целевому комитету Rich Mathematical Task Committee, а также их коллегам, которые поддержали эту работу в своих подразделениях.
Комитет VDOE Rich Mathematical Task Committee, состоящий из руководителей учителей математики со всего Содружества, создал математически насыщенные задачи, соответствующие Стандартам обучения по математике от 2016 года . Комитет создал шаблоны реализации задач до того, как приступить к их администрированию в классах. Для многих задач комитет оценивал задачи индивидуально, откалибровал их оценку с командой, предоставил обоснование выставления оценок и отобрал студенческие работы, которые будут служить в качестве якорных документов.Департамент образования Вирджинии хотел бы выразить особую благодарность Целевому комитету Rich Mathematical Task Committee, а также их коллегам, которые поддержали эту работу в своих подразделениях.
Планирование удаленного выполнения сложных математических задач
Эти ресурсы, наряду с руководством по планированию удаленного выполнения сложных математических задач, предназначены для поддержки учителей во внедрении Стандартов обучения по математике на 2016 год в своих классах.Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.
Вебинары для поддержки удаленного выполнения сложных математических задач
Выполнение сложных математических задач в классе K-2
Выполнение сложных математических задач в классе 3–5 классов
Выполнение сложных математических задач в 6-8 классах
Выполнение сложных математических задач в 9–12 классах
Детский сад
Building Towers Task
Задача по сбору яблок
Задача совместного использования файлов cookie
Загадки формы Task
Задача смешанных блоков
Утреннее рутинное задание
Вернуться к началу
1 марка
Задача сравнения точек
Игрушечные машинки Task
Задача «Прогулка на природе»
Задание на удвоение игры
Игра с паттернами, задание
Как они могут быть равными? Задача
Вернуться к началу
2 класс
Mystery Number Task
Наклейка устанавливает задание
Браслет Task
Сковороды для брауни Task
Talking Sticks Task
Монеты в кармане Задание
Сколько таблиц Задача
Количество учеников Задание
Вернуться к началу
3 класс
Задание для упаковки карандашей
Задание на вечеринку с пиццей
Карнавальные призы Задание
Корзины яблок Task
Деньги в копилке Задача
Полигональные пазлы Задача
Вернуться к началу
4 класс
Специальное задание по доставке
Тако вторник, задание
Транспортное задание поездки
Задание заливки красок
Обед у Леонардо.

Задача комбинаций кемпинга
Исследование четырехугольников, задание
Задача о возможностях равенства
Вернуться к началу
5 класс
Сохранение для велосипедного задания
Комната для обуви Задача
Задача времени смешивания трассы
Шина A или шина B Задача
Задача на проектирование углов
Разработка задачи Windows
Вернуться к началу
6 класс
Задание на победу в игре
Задача пополнения печенья
Задача умного покупателя
Задача по отслеживанию акул
Задание на проектирование парка для собак
Задание по доставке пиццы
Задача экранного времени
Вернуться к началу
7 класс
Какое задание микроскопа
Задача по сбору средств для продажи выпечки
Задание на транспортировочную коробку
Задание «Прогулка по парку»
Задача отжима, отжима, отжима
Летнее задание
Задача по садоводству
Вернуться к началу
8 класс
Задача дилеммы директора
Задача преобразования монстров
Задача самого длинного пути
Задача «Ваш счастливый день»
Арахисовое масло Задание
Сколько камней мне понадобится Задача
Вернуться к началу
Алгебра I
Задача по переводу покупок
Цветочные сады, задание
Забавное задание на качелях
Задача на полную парковку
Radical Rocks Task
The Trampoline PartyTask
Задача сбережения велосипедов
Задача соревнований по футболу
Мы играем в баскетбол, задание
Вернуться к началу
Геометрия
Задача логических драйверов
Линии и тигры и медведи, о боже! Задача
Задача авиашоу
Take Me Out to the Ball Game Task
Sea Cities Task
Задача встряхивания, дребезжания и перекатывания
Вернуться к началу
Алгебра II
Задача лучшего друга дрона
Функция задания на поездку
Задача анимации It
Задача по лесным пожарам
Задача атаки водорослей
Вернуться к началу
Шаблон пустого задания
Богатая математическая задача Рубрика
Благодарности
Министерство образования Вирджинии выражает особую благодарность Целевому комитету Rich Mathematical Task Committee, а также их коллегам, которые поддержали эту работу в своих подразделениях.
- Кэндис Баркли, Государственные школы округа Хенрико
- Джессика Браун, Государственные школы округа Глостер
- Kaitlyn Bookbinder, Государственные школы округа Хенрико
- Эйприл Кук, Государственные школы округа Фэйрфакс
- Келли Дэй, Государственные школы города Вирджиния-Бич
- Мишель Делоач, Государственные школы округа Честерфилд
- Эллисон Кришер ДеПиро, Государственные школы города Вирджиния-Бич
- Кейтлин Девайн, Государственные школы округа Хенрико
- Дженна Филипович, Государственные школы города Вирджиния-Бич
- Крис Гушу, Государственные школы округа Принц Уильям
- Келли Халпин, Государственные школы округа Фэйрфакс
- Эндиа Хэтчер, Государственные школы Портсмута
- Мелани Дженкинс, Государственные школы округа Глостер
- Дженни Джонс, Государственные школы округа Ганновер
- Тиша Джонс, Государственные школы Портсмута
- Лесли Ладен, Государственные школы округа Стаффорд
- Кимберли Лоуренс, Государственные школы округа Ганновер
- Линн Мид, Государственные школы округа Хенрико
- Кэтрин Мансон, Государственные школы округа Честерфилд
- Анна Папас, Государственные школы округа Стаффорд
- Сара Портер, Государственные школы Саффолка
- Кэндис Стэндли, Государственные школы округа Калпепер
- Донна Снайдер, Государственные школы города Роанок
- Холли Тейт, Государственные школы города Александрия
- Дэвид Ванвлит, Государственные школы округа Фэйрфакс
Начало страницы
Разъяснение, классификация и выбор подходящих задач для различных типов обучения и оценки
27
Министерство образования Сингапура. (2004). Руководство по оценке неполной средней школы
(2004). Руководство по оценке неполной средней школы
по математике. Сингапур: Отдел планирования и разработки учебных программ.
Москкович, Дж. Н. (2002a). Введение в изучение повседневных и академических
математических практик. В Э. Якель (серия ред.) И М. Э. Бреннер и Дж. Н. Москкович
(ред. Монографии), Повседневная и академическая математика в классе (стр. 1-11).
Рестон, Вирджиния: Национальный совет учителей математики.
Москкович, Я.Н. (2002b). Объединение рабочего места и академической математической практики
во время оценивания в классе. В E. Yackel (Series Ed.) И M. E. Brenner & J.
N. Moschkovich (Monography Eds.), Повседневная и академическая математика в классе
(стр. 93-110). Рестон, Вирджиния: Национальный совет учителей математики.
Национальный совет учителей математики. (1980). Программа действий: Рекомендации
по школьной математике 80-х годов.Рестон, Вирджиния: Национальный совет учителей математики
.
Национальный совет учителей математики. (1991). Профессиональные стандарты обучения математике
. Рестон, Вирджиния: Национальный совет учителей математики.
Нейланд Дж. (1994). Разработка богатой математической деятельности. В J. Neyland (Ed.), Mathematics
education: A Handbook for Teacher (Vol. 1, pp. 106-122). Веллингтон, Новая Зеландия:
Педагогический колледж Веллингтона.
Ортон, А., и Фробишер, Л. (1996). Понимание преподавания математики. Лондон: Касселл.
Пири С. (1987). Математические исследования в классе: пособие для учителей.
Бейзингсток, Великобритания: Macmillan.
Поуп Р. (2005). Творчество: теория, история, практика. Лондон: Рутледж.
Рейс Р. Э., Линдквист М. М., Ламбдин Д. В., Смит Н. Л. и Суйдам М. Н. (2004).
Помощь детям в изучении математики (7-е изд.).Хобокен, Нью-Джерси: Джон Уайли и сыновья.
Schoenfeld, A.H. (1985). Решение математических задач. Орландо, Флорида: Academic Press.
Орландо, Флорида: Academic Press.
Шенфельд А. Х. (1988). Когда хорошее преподавание приводит к плохим результатам: Катастрофы курсов математики с «хорошо преподаваемым
». Психолог-педагог, 23, 145-166.
Шеффилд, Л. Дж., Мейснер, Х. и Фунг, П. Ю. (2004, июль). Развитие математических
творческих способностей детей раннего возраста. Документ, представленный на Десятом международном конгрессе по математическому образованию
, Копенгаген, Дания.
Сильвер, Э.А. (1994). О постановке математической задачи. Для изучения математики,
14 (1), 19-28.
Саймон, Х. А. (1973). Структура плохо структурированных задач. Искусственный интеллект, 4, 181-
201.
Саймон, Х. А. (1978). Теория обработки информации для решения человеческих проблем. В W. K.
Estes (Ed.), Справочник по обучению и когнитивным процессам (Том 5, стр. 271-295).
Хиллсдейл, Нью-Джерси: Эрлбаум.
Skovsmose, O.(2002). Пейзажи следствия. В Л. Хаггарти (ред.), Преподавание
математики в средних школах (стр. 115-128). Лондон: РутледжФалмер.
Stempien, M., & Borasi, R. (1985). Письменные работы студентов по математике: некоторые идеи и
опыта. Для изучения математики, 5 (3), 14-17.
Таннер, Х. (1989). Представляем расследования. Обучение математике, 127, 20-23.
Тех, К. С., & Ло, К. Ю. (2007). Новая программа дополнительной математики (8-е изд.). Сингапур:
Шинг Ли.
Тех, К. С., Ло, К. Ю., Йео, Дж., И Чоу, И. (2007). Новая учебная программа по математике 1:
Альтернативная оценка и компакт-диск включены. Сингапур: Шинг Ли.
Теонг, С. К. (2002). Исследовательский подход к преподаванию и изучению математики. Педагог по математике
, 6 (2), 32-46.
Торранс, Э. П. (1984). Торранс тесты творческого мышления (Новая ред.). Бенсенвилл, Иллинойс:
Служба школьного тестирования.
Ресурсы по алгебре I — Математический центр Кентукки
KCM хочет помочь учителям создать мыслящие сообщества в своих классах математики. Вместо того, чтобы обучать алгебре процедурно, мы предлагаем вам помочь вашему ученику меньше сосредотачиваться на том, что он должен делать дальше, и больше на активном осмыслении математики. Использование сложных математических задач — это одна из стратегий, которую преподаватели алгебры могут реализовать, чтобы привлечь учащихся и сформировать в классе культуру мышления, которая фокусируется на алгебраических рассуждениях и осмыслении.
Вместо того, чтобы обучать алгебре процедурно, мы предлагаем вам помочь вашему ученику меньше сосредотачиваться на том, что он должен делать дальше, и больше на активном осмыслении математики. Использование сложных математических задач — это одна из стратегий, которую преподаватели алгебры могут реализовать, чтобы привлечь учащихся и сформировать в классе культуру мышления, которая фокусируется на алгебраических рассуждениях и осмыслении.
Богатые задачи: развитие глубоких математических рассуждений у учащихся
Богатые математические задания вовлекают учащихся в изучение, наблюдение, обсуждение, предположение, объяснение, обобщение, убеждение и настойчивость. Студенты сосредотачиваются на математике, в то время как учитель сосредотачивается на наблюдении и поддержке учащихся в их собственных открытиях. Сама по себе сложная задача небогата, если только классная культура не является такой, в которой учащиеся не являются пассивными получателями знаний, а скорее являются любопытными, рефлексивными конструкторами своего собственного понимания.
Заданий по богатой математике:
- Доступно для всех учащихся («низкий пол, высокий потолок»)
- Задача или приложение из реальной жизни
- Множественные подходы и представления
- Сотрудничество и обсуждение
- Вовлеченность, любопытство и творчество
- Установление связей внутри и / или между темами и областями [Булер, «Математическое мышление»]
- Возможности расширения
Предложения по реализации сложных задач
- Студенты работают с партнером
- Задача представлена студентам, и студентам дается время, чтобы они разобрались в проблеме.
- Какие нормы необходимо установить, чтобы учащиеся чувствовали себя в безопасности при попытках?
- Каким образом студенты будут постоянно участвовать в обучении?
- Учащимся дается время для работы над заданием, а учитель вращается по группам, задавая вопросы и поощряя продуктивную борьбу.
 Учитель не указывает дальнейшие шаги и не дает ответов.
Учитель не указывает дальнейшие шаги и не дает ответов.- Какие ободряющие / вызывающие / полезные (но не директивные) ответы могут быть у учителя, когда ученики застревают?
- Смогут ли все учащиеся участвовать в осмысленном изучении математики? Могут ли ученики прятаться или игнорироваться?
- Студенческим парам предлагается исследовать и генерировать уникальные решения. Они также должны обосновать свои аргументы в пользу своего выбора.
- Каким образом студенты будут приглашены для объяснения своего мышления?
- Каким образом учащимся будет предоставлена возможность с уважением бросить вызов другим или отстаивать свою точку зрения?
- Учитель использует задание как возможность для формирующего оценивания.
- Как инструкция будет реагировать на идеи студентов?
- Какие возможности будут у студентов для демонстрации своего обучения?
- Учитель организует заключительное обсуждение всего класса, подчеркивая различные математические связи и мыслительные процессы, которые использовались при решении задачи.
- Каким образом мышление учащихся будет включено в обсуждения в классе?
- Какие возможности будут у студентов для объяснения своих идей? Каким образом их идеи будут опираться на другие?
Пример расширенных задач
Другие источники для сложных задач алгебры
Учебные программы
Примеры уроков
Статья: Джеймс У.Стиглер и Джеймс Хиберт
Статья: «Урок подобен стремительной реке» Кэтрин К. Льюис и Инеко Цучида
Глава книги: Мощное решение проблем: упражнения для осмысления с помощью математических практик Макс Рэй
Статья: «Обдумывание урока: успешное выполнение задач высокого уровня» Маргарет С. Смит, Виктория Билл и Элизабет К. Хьюз
Статья: «Привычки ума: Организационный принцип для учебной программы математики» Аль Куоко, Э. Пол Голденберг и Джун Марк
Пол Голденберг и Джун Марк
Использование проблем и сложных задач — Ipu Kererū
Джуди Бейли, Университет Вайкато
За последний год ряд международных учителей математики и исследователей посетили Новую Зеландию, чтобы поработать с учителями над использованием сложных задач и решением математических задач. Совсем недавно профессор Джо Булер исследовал концепции математической свободы и разнообразных задач с примерно 500 учителями на однодневном семинаре в Гамильтоне.
Эти подходы к обучению математике вызывают большой интерес, но могут быть и реальные проблемы. Преподавание математики с использованием сложных заданий или математических задач может означать значительный сдвиг в практике (и мышлении!) Для учителей, которые часто лично сталкивались с математикой как с довольно сухой дисциплиной, включающей в себя набор процедур изучения. Может быть трудно изменить свою практику, когда ваш собственный опыт и убеждения по предмету отличаются от тех, которые предлагаются (или даже требуются) национальной учебной программой. В этом сообщении в блоге исследуются некоторые ключевые изменения, связанные с обучением посредством сложных задач и решения проблем, а также представлены некоторые практические советы и ресурсы для учителей, которые только начинают или уже находятся в этом пути.
Что такое математика? Если вы учитель математики (начальной или средней) и думаете об адаптации своей практики, полезно подумать о том, что вы думаете о природе математики — , что такое на самом деле? Спросите нескольких людей: «Что такое математика?», И вы, вероятно, получите комментарии о том, что математика (а) связана с числами и (б) что-то, «в чем они не разбираются».Люди могут делиться своими воспоминаниями о выполнении многих и, по-видимому, бессмысленных упражнений из школьного учебника. Такой опыт и идеи могут привести к тому, что математика будет рассматриваться как совокупность знаний, содержащих истины, касающиеся количества, закономерностей, формы, пространства и случайности. Для учителей, придерживающихся этой веры, преподавание и изучение математики, вероятно, связано с передачей «правил» и попыткой передать и / или понять заранее определенные, фиксированные идеи. Такие уроки могут быть тем, что Фостер (2013) назвал «тройными» уроками, где учитель ex plain, а затем ученики выполняют ex amples и ex ercises.
Для учителей, придерживающихся этой веры, преподавание и изучение математики, вероятно, связано с передачей «правил» и попыткой передать и / или понять заранее определенные, фиксированные идеи. Такие уроки могут быть тем, что Фостер (2013) назвал «тройными» уроками, где учитель ex plain, а затем ученики выполняют ex amples и ex ercises.
Другой способ думать о математике — это рассматривать математику как конструктивную, творческую, социальную деятельность . Когда учителя придерживаются этой веры, ожидается, что учащиеся будут сами исследовать и находить идеи. Мало кто (за исключением, возможно, тех, кто еще не достиг школьного возраста!), Рассматривал бы идеи творчества, воображения и удивления в сочетании со словом «математика». Однако я вспоминаю случай с моим 22-месячным внуком. Мне нравилось наблюдать, как он почти час загружал фейхоа в двигатель своего трактора (была небольшая полость, в которую можно было положить вещи), перекладывал камни на верхнюю часть двигателя трактора (фейхоа теперь немного сдавливались!), А затем принимал камни и бросить их на лужайку! Он выслушал объяснение своей бабушки о том, что нельзя оставлять камни на лужайке, и ответил на них, поскольку это может повлиять на газонокосилку его родителей.Игра была творческой, сфокусированной, сконцентрированной, социальной и перемежалась с обучением управлению трактором, поскольку Нана услужливо обеспечивала мощность двигателя. Возможности для обучения включали пространственное осознание, объем, «больше» (любимое слово) и социальные конструкции, такие как мышление о других. Математические понятия (и другие) изучались творчески, творчески и в игровой форме. Чудесно!
Преподавание математики как творческое, творческое и прекрасное: важность подлинных задач Если идея о том, что математика является творческой, образной и замечательной для наших учеников (любого возраста), привлекает, может возникнуть вопрос: как мы можем преподавать математику таким образом? Мощный способ двигаться вперед встроен (хотя, возможно, его легко упустить из виду) в Новозеландский учебный план для школ с английским языком обучения в основе каждого набора целей по математике от уровней 1 до 8. На всех уровнях учебной программы эта основа гласит:
На всех уровнях учебной программы эта основа гласит:
«в ряде значимых контекстов учащиеся будут заниматься математическим и статистическим мышлением. Они будут решать проблемы [выделено мной] и моделировать ситуации, которые требуют от них:… ».
Для тех, кто помнит MiNZC, предыдущую учебную программу по математике, идея решения математических задач, лежащая в основе математики, не нова. Однако, никогда по-настоящему не испытав на себе радости (и проблем) реального решения проблем, я вспоминаю, как я (как классный учитель) относил « решение проблем » к случайному вечеру пятницы или окончанию урока — однажды якобы «настоящая» (читай «тройные уроки») математика была сделана.Оглядываясь назад, я теперь вижу проблемы с этим подходом: я все еще в основном говорил своим ученикам, что математика — это воспроизведение индивидуальных, несвязанных процедур, и, тратя минимум времени на решение задач, я не давал ученикам достаточной возможности для развития. их настоящие математические «мускулы».
Итак, если примеры и упражнения не проблема, то что? Главная особенность реальной проблемы состоит в том, что для решающего проблемы нет известных способов ее решения. Если учитель продемонстрировал процедуру на доске, на самом деле «проблемы» нет. Богатая задача имеет много общего с математическими задачами, в которых основное внимание уделяется исследованию, и есть несколько методов, путей и / или представлений, которые относятся к задаче. Богатая задача часто имеет «низкий пол» и «высокий потолок», что означает, что задача доступна для широкого круга учащихся.
Проблемное обучение в действии Как выглядит решение математических задач или использование сложных задач в действии? Это означает, что учащиеся, скорее всего, не сразу поймут, что им делать, и что мы, как учителя, должны научиться сначала отступать и доверять учащимся творческие способности, творческие способности и решение проблемы или задачи.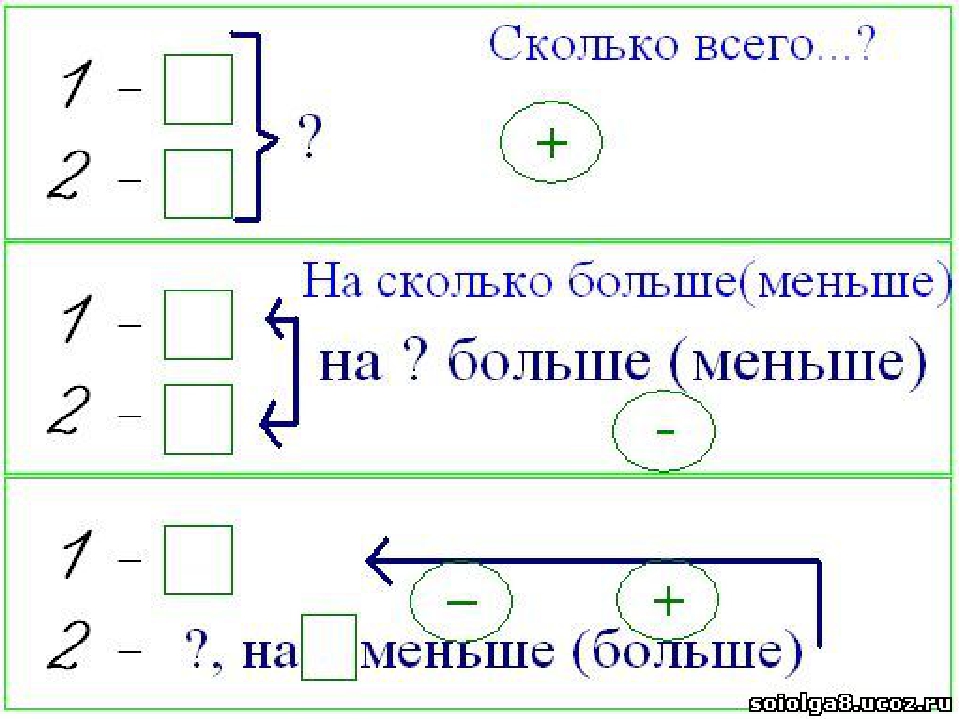 Сначала, конечно, нам придется обучать наших учеников этому новому опыту и устанавливать новые нормы для нашего класса математики — например, помогать ученикам понять, что это нормально — не сразу знать, как решить задачу; что мы будем работать вместе, чтобы увидеть, какого прогресса мы можем добиться; что мы будем ценить вклад друг друга в этот процесс; и что учитель не «спасет» их, как только они попросят о помощи. Существуют полезные рамки для поддержки учителей в обучении, чтобы облегчить такие уроки — e.грамм. см. здесь и здесь.
Сначала, конечно, нам придется обучать наших учеников этому новому опыту и устанавливать новые нормы для нашего класса математики — например, помогать ученикам понять, что это нормально — не сразу знать, как решить задачу; что мы будем работать вместе, чтобы увидеть, какого прогресса мы можем добиться; что мы будем ценить вклад друг друга в этот процесс; и что учитель не «спасет» их, как только они попросят о помощи. Существуют полезные рамки для поддержки учителей в обучении, чтобы облегчить такие уроки — e.грамм. см. здесь и здесь.
Международные исследования, примеры передовой практики здесь, в Аотеароа, Новая Зеландия, а также мой собственный опыт и исследования в различных классах Новой Зеландии — все это показывает, что проблемно-ориентированное преподавание математики привлекает детей . Например, недавно я стал свидетелем этого в большой современной учебной среде, в которой участвовало 60 детей, из которых были заняты одной проблемой «низкий пол, высокий потолок». Задача, которая использовалась в этом уроке, воспроизводится ниже — многие учителя признают ее классической задачей по математике.
Такие задачи и задачи требуют времени (по крайней мере, целый урок или больше для одной проблемы / задачи) и вовлекают учащихся в игру с рядом идей (некоторые из которых не работают), индивидуальную работу и небольшие группы, общение с другие, оправдывая и объясняя ваше мышление, борьбу и настойчивость. Возможностей для связи с ключевыми компетенциями учебной программы Новой Зеландии, а также с устремлениями Те Мараутанга о Аотеароа предостаточно.
Как учителя могут научиться преподавать, используя задачи и сложные задания?Изменение вашего обучения может быть трудным и трудным, но при этом полезным и воодушевляющим.Итак, , как научиться преподавать математику таким образом? На ум приходят три вещи.
Во-первых, учителям полезно лично испытать решение проблем или участие в сложных задачах , то есть фактически самостоятельно заниматься решением математических задач. Это может означать поиск подходящих возможностей профессионального развития, где вы не только расскажете о этих педагогических методиках, но и получите возможность взять на себя роль учеников и испытать их изнутри.
Это может означать поиск подходящих возможностей профессионального развития, где вы не только расскажете о этих педагогических методиках, но и получите возможность взять на себя роль учеников и испытать их изнутри.
Во-вторых, исследования показывают, что , работая совместно с другими учителями , является эффективным способом узнать и осмыслить свое преподавание. Это говорит о том, что следующим шагом может быть поиск заинтересованного коллеги по преподаванию, определение подлинной проблемы для вас обоих (попробуйте поискать здесь, здесь или здесь) и начать работу. После успешного решения проблемы (обратитесь за помощью, если вы застряли — это все), подумайте, что этот опыт может означать для преподавания и изучения математики.
В-третьих, обучение математике как творческое занятие требует, чтобы мы доверяли детям и считали их способными и компетентными в решении задач. К сожалению, некоторые дети уже укоренились в бесполезных представлениях о математике — например, что математика — это внешняя совокупность заранее определенных, фиксированных и сложных идей или что математика — это способность быстро получать правильные ответы. Чтобы преодолеть эти убеждения, с нашей стороны может потребоваться некоторое умышленное бездействие и настойчивость.Недавние работы по развитию математического мышления и установлению положительных убеждений в математике могут быть здесь полезны, побуждая студентов познать себя как способных и компетентных математиков.
Восемнадцать месяцев назад мы стали свидетелями прекращения обязательного использования национальных стандартов и освобождения от связанного с этим давления, которое эта политика оказывала на учащихся, родителей, учителей и школы. Это изменение дало нам возможность пересмотреть наши математические программы.Учителя, с которыми я разговаривал, выразили удовлетворение отменой обязательных требований национальных стандартов, объяснив, что они видят в этом возможность предложить учащимся более творческий математический и интегрированный учебный план.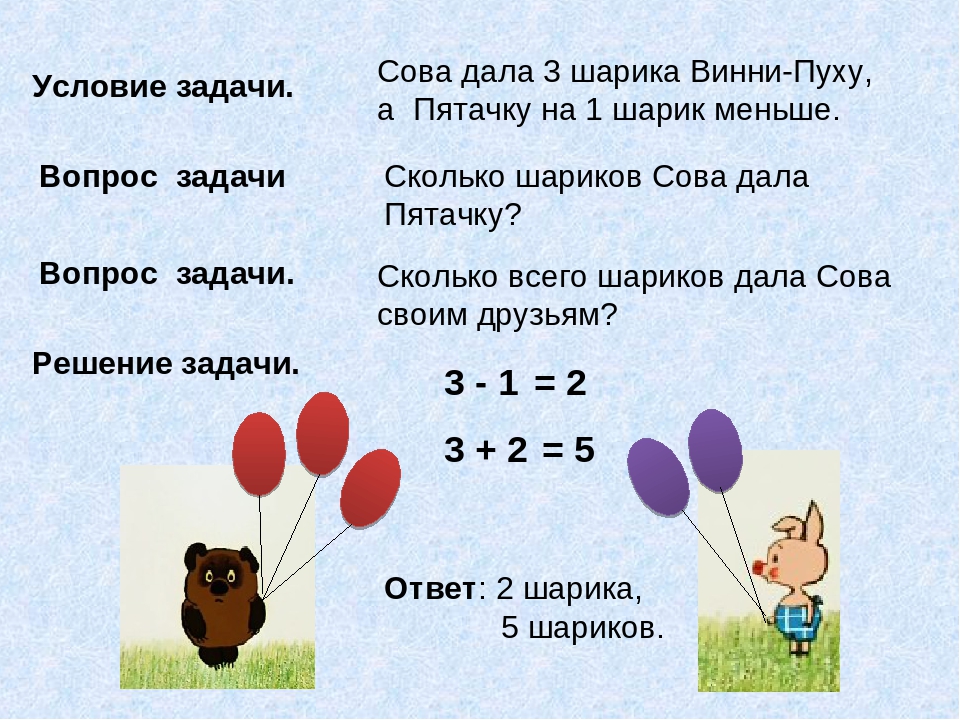
 В нашем курсе мы много внимания уделим именно записи решений. В каждом письменном конспекте приведены примеры оформления решений. Если в качестве решения контрольной работы присылать только ответы, то оценка будет низкой.
В нашем курсе мы много внимания уделим именно записи решений. В каждом письменном конспекте приведены примеры оформления решений. Если в качестве решения контрольной работы присылать только ответы, то оценка будет низкой. Небольшой минус — тесты часто получаются похожими друг на друга.
Небольшой минус — тесты часто получаются похожими друг на друга. Например, математика, имеющая связь с литературой, может быть очень интересной и увлекательной для учащихся, несмотря на то, что исследуемые сценарии нельзя назвать «действительно реальными». Помните, что цель состоит в том, чтобы представить задания, которые интересны и могут помочь учащимся понять, что концепции, которые они изучают в своих классах математики, не полностью отделены от их жизни вне класса. Не подавляйте свое творчество, налагая ложные ограничения на то, что является «реальным» приложением.Студенты будут вовлечены в проблемы, которые возникают из литературы, из других предметных областей и из их воображения, а также из их «действительно реальной» жизни!
Например, математика, имеющая связь с литературой, может быть очень интересной и увлекательной для учащихся, несмотря на то, что исследуемые сценарии нельзя назвать «действительно реальными». Помните, что цель состоит в том, чтобы представить задания, которые интересны и могут помочь учащимся понять, что концепции, которые они изучают в своих классах математики, не полностью отделены от их жизни вне класса. Не подавляйте свое творчество, налагая ложные ограничения на то, что является «реальным» приложением.Студенты будут вовлечены в проблемы, которые возникают из литературы, из других предметных областей и из их воображения, а также из их «действительно реальной» жизни!
 (NCTM 2000, стр. 19).
(NCTM 2000, стр. 19). nctm.org/uploadedFiles/Research_News_and_Advocacy/Research/Clips_and_Briefs/Research_brief_14_-_Problem_Solving.pdf. Загружено 30 декабря 2012 г.
nctm.org/uploadedFiles/Research_News_and_Advocacy/Research/Clips_and_Briefs/Research_brief_14_-_Problem_Solving.pdf. Загружено 30 декабря 2012 г. Учитель не указывает дальнейшие шаги и не дает ответов.
Учитель не указывает дальнейшие шаги и не дает ответов.