ВСЕ ОСНОВНЫЕ ВИДЫ И ТИПЫ ЗАДАЧ. Сайт О. Узоровой
Методика Узоровой — Нефедовой по решению всех видов составных задач
Все основные виды и типы задач по математике всех Федеральных программ начальной школы
Части любой задачи для любого класса
Выучить и знать всегда
ЦЕПОЧКА РАССУЖДЕНИЙ
После нахождения опорных слов, составления краткой записи или чертежа мы настоятельно рекомендуем ЛЮБУЮ задачу начинать решать С КОНЦА, то есть с ВОПРОСА. Эта СИСТЕМАТИЧЕСКАЯ ЦЕПОЧКА РАССУЖДЕНИЙ приведет ребёнка к правильному решению ЛЮБОЙ ЗАДАЧИ.
В приведённых ниже разборах задач ЦЕПОЧКА РАССУЖДЕНИЙ сначала идёт после слов: Рассуждай так.
Потом ЦЕПОЧКА РАССУЖДЕНИЙ превращается в схему типа:
Осталось Ушло
Как составлялась эта схема? Была задача:
Во дворе гуляли 16 ребят. Сначала домой ушли 6 девочек, а потом 3 мальчика. Сколько ребят осталось во дворе?
Пошаговый образец рассуждения вслух ребёнка
Решаем с конца, с вопроса.
— что спрашивается в задаче?
— сколько ребят осталось.
— значит, первое слово в цепочке пишем — осталось.
Осталось
— чтобы узнать, сколько осталось, надо знать, сколько БЫЛО и сколько УШЛО. Сколько БЫЛО, мы знаем, сколько УШЛО – не знаем, значит, в цепочке дописываем слово «ушло».
Осталось Ушло
— так как в цепочке ДВА СЛОВА, то в задаче ДВА ДЕЙСТВИЯ.
РЕШАЕМ ЗАДАЧУ, РАСКРУЧИВАЕМ ЦЕПОЧКУ С КОНЦА.
— Первое слово с конца – УШЛО, значит, сначала узнаем, сколько ребят УШЛО:
6 + 3 = 9 (р)
— Второе слово в цепочке – «осталось». Значит, вторым действием мы отвечаем на главный вопрос задачи и узнаём, сколько ребят осталось.
16 – 9 = 7 (р)
Почему так важна ЦЕПОЧКА РАССУЖДЕНИЙ, которая пишется слева направо,
а раскручивается с конца, справа налево при решении КАЖДОЙ ЗАДАЧИ?
- Потому что ТОЛЬКО при ТАКОМ систематическом ПОДХОДЕ ваш ребёнок сможет решать ЛЮБУЮ ЗАДАЧУ в начальной и средней школе, экономя вам лично время, силы и нервы.
- Потому что это развивает логику ребёнка
- Потому что такая ЦЕПОЧКА РАССУЖДЕНИЙ развивает ВСЕГО ребёнка по ВСЕМ НАПРАВЛЕНИЯМ.
P.
Вы можете скачать
- условия задач,
- их решения,
- правильное оформление,
- краткую запись и чертежи БЕСПЛАТНО.
Справочный материал «Классификация задач по математике»
КЛАССИФИКАЦИЯ ЗАДАЧ
В зависимости от того, описывается в задаче жизненная ситуация или нет, математические задачи делятся на сюжетные (текстовые) и бессюжетные
Текстовые задачи, в зависимости от того, во сколько действий решаются, бывают простыми и составными. Простые задачи решаются в одно действие, а составные в два и более действий.
Рассмотрим разные классификации простых задач.
В зависимости от структуры М.И. Моро и А.М. Пышкало выделяют следующие группы простых задач:
Первая группа задач – задачи, направленные на раскрытие конкретного смысла арифметических действий (сложение, вычитание, умножение и деление). Таких задач – 5 видов:
— на нахождение суммы;
— на нахождение остатка;
— на нахождение суммы одинаковых слагаемых;
— на деление по содержанию;
— на деление на равные части.
Вторая группа – задачи, раскрывающие различные отношения между числами. Их 10 видов:
– на увеличение (уменьшение) числа на несколько единиц, прямая форма;
— на увеличение (уменьшение) числа на несколько единиц косвенная форма;
на увеличение (уменьшение) числа в несколько раз, прямая форма;
на увеличение (уменьшение) числа в несколько раз, косвенная форма;
на разностное сравнение;
на кратное сравнение.
Третья группа – задачи, раскрывающие связи между компонентами и результатами арифметических действий. Сюда входят 6 видов простых задач:
на нахождение неизвестного слагаемого;
на нахождение неизвестного уменьшаемого;
на нахождение неизвестного вычитаемого;
на нахождение неизвестного множителя;
на нахождение неизвестного делимого.
Четвёртая группа — задачи на сравнение.
Для удобства восприятия эти виды задач расположены в таблице (приводится ниже).
Группы задач | Задачи на усвоение конкретного смысла действий | Задачи на нахождение неизвестных компонентов действий | Задачи на увеличение (уменьшение) числа на несколько единиц (в несколько раз) | Задачи на сравнение |
Задачи на сложение |
? II п. — 4 кн. (задача на нахождение суммы) | Было – ? Убрали — 4 кн. Осталось — 5 кн. (задача на нахождение неизвестного уменьшаемого по известным вычитаемому и разности) | I полка -14 кн., II полка -?, на 2 кн. больше (Задача на увеличение числа на несколько единиц, прямая форма) I п. -14 кн., это на 2 кн. меньше II п. — ? (Задача на увеличение числа на несколько единиц, косвенная форма) | |
Задачи на вычитание | Было — 9 кн, Убрали — 4 кн. Осталось — ? (Задача на нахождение остатка) | Было – 9 кн. Убрали — ? Осталось — 5 кн. (Задача на нахождение неизвестного вычитаемого по известным уменьшаемому и разности)
? II п. — 4 кн. (задача на нахождение неизвестного слагаемого по известным сумме и другому слагаемому) | I полка — 14 кн, II полка — ?, на 2 книги меньше ( Задача на уменьшение числа на несколько единиц, прямая форма) I полка — 14 кн., это на 2 книги больше II полка — ? (Задача на уменьшение числа на несколько единиц, косвенная форма) | I п. -14 кн. на ? II п. –28кн
(Задача на разностное сравнение) |
Задачи на умножение | Сколько колес у трех двухколесных велосипедов? (Задача на нахождение суммы одинаковых слагаемых) | Неизвестное число разделили на 5. Получили 3. Найти неизвестное число. (Задача на нахождение неизвестного делимого по известным делителю и частному) | I полка -14 кн. II полка – ?, в 2 раза больше (Задача на увеличение числа в несколько раз, прямая форма) 1полка — 14 кн., это в 2 раза меньше II полка — ? (Задача на увеличение числа в несколько раз, косвенная форма) | |
Задачи на деление | 15 морковок разделили нескольким кроликам по 5 морковок. Сколько кроликов получили морковки? (Задача на деление по содержанию) 15 морковок разделили 3 кроликам поровну. По сколько морковок получил каждый кролик? (Задача на деление на равные части) | Неизвестное число умножили на 5. Получили 15. Найти неизвестное число. (Задача на нахождение неизвестного множителя) Число 15 разделили на неизвестное число и получили 3. Найти неизвестное число. ( Задача на нахождение неизвестного делителя) | 1полка -14 кн. II полка — ?, в 2 раза меньше (Задача на уменьшение числа в несколько раз, прямая форма) 1полка — 14 кн., это в 2 раза больше II полка — ? (Задача на уменьшение числа в несколько раз, косвенная форма) | Iп. -14 кн. Во? IIп. –28кн. (Задача на кратное сравнение) |
Приведенная классификация удобна. Она позволяет выбирать способ решения задачи в зависимости от ее структуры, то есть, характера взаимосвязи между данными и искомыми задачи и на этой основе строго обосновывать выбор решения.
Классификации текстовых задач по математике.
Если говорить о классификации задач, то необходимо для начала определить, из каких компонентов она состоит и на какие этапы можно разделить процесс решения задачи.
В методике преподавания математике процесс решения текстовых задач делят на четыре типа:
1)Понимание условия задачи.
Это самый главный этап в решении задачи, так как учащиеся должны понимать, что дано в условии и что требуется в задаче. Они должны осмыслить отдельные элементы условия, после этого они производят поиск необходимой информации в своей памяти, и сопоставить с известной информацией условие и заключение задачи.
2) Составление плана решения.
Учащимся необходимо разработать целенаправленные действия всевозможных сочетаний из данных и искомых, довести задачу к известному типу, выбрать для решения самый оптимальный метод и наметить для себя план решения.
3)Реализация плана решения.
В этом этапе учащиеся почти выполняют план решения, с последовательной корректировкой через взаимоотношения с условием и выбранным методом, выбирают подходящий способ для оформления решения и оформляют его.
4) Исследование найденного решения.
Учащиеся делают акцент на конечном результате решения задачи, анализируют его, по необходимости проводят исследование особых и частных случаев.
В педагогической литературе имеются разнообразные подходы к классификации задач (по Ю.М. Колягину, Г.В. Дорофееву и др.). Разберём некоторые из них:
Ю.М. Колягин выделяет следующие задачи по количеству неизвестных компонентов в структуре задачи:
а) Задачи обучающие (в этих задачах содержится один неизвестный компонент).
Эти задачи он еще делит:
с неизвестными первоначальными данными (например: известны корни квадратного уравнения, и нужно найти само уравнение).
с неизвестными теоретическими данными (например: нужно найти ошибку в решении задачи).
с неизвестными алгоритмом самого решения (например: в записи 1*2* 5* 4* 3 заменить вместо звездочек знаки и расставить скобки так, что бы получилось выражение, значение которого равно 9)
с неизвестным конечным результатом (например: найти значение выражения).
б) Задачи поискового вида (это те задачи, в которых неизвестно два компонента).
в) Проблемные задачи (это задачи, в которых неизвестно три компонента).
Если рассматривать, как задачи относятся к теории то можно выделить стандартные и нестандартные задачи.
Рассмотрим на примере стандартные задачи:
1. Первый мотоциклист за 3 часа проехал на 36км больше, чем второй за 2 часа. Найдите скорость каждого, если скорость второго мотоциклиста на 25 км/ч меньше скорости первого.
2. Для детей 10 лет наиболее полноценным является питание, если пища содержит 10% животных белков, 5% растительных белков, 17% животного жира, 3% растительного жира и 64% углеводов. По этим данным построить круговую диаграмму.
Рассмотрим на примере нестандартные задачи:
1. Три друга – Максим, Илья, Саша, преподают различные предметы (математику, русский язык, историю) в школах Ялты, Симферополя и Евпатории. Известно, что Максим преподает не в Ялте, а Илья не в Симферополе. Ялтинец преподаёт не историю, а тот, кто работает в Симферополе, преподает математику, Илья преподает не русский язык. Какой предмет, и в каком городе преподаёт каждый из товарищей?
Сравнение задач с компонентами учебно-познавательной деятельности приводит к такой классификации:
задачи, которые стимулируют учебно-познавательную деятельность школьников;
задачи, которые организуют и реализовывают учебно-познавательную деятельность;
задачи, при выполнении которых исполняется проверка и самопроверка результативности учебно-познавательной деятельности.
По своему математическому содержанию, соответствующей специфике той или другой математической дисциплины, задачи можно разделить на: алгебраические, арифметические, геометрические, аналитические.
По содержанию задачи группируют на:
задачи на движение,
задачи на части,
задачи на проценты и так далее,
внутри каждого образа в зависимости от логической структуры задачи разделяют следующие виды задач:
задачи на встречное движение в одну сторону и в противоположные стороны,
задачи на нахождение части целого и целого по его части,
задачи на нахождение соотношения чисел,
задачи на нахождение процента от числа и числа по его проценту,
задачи на нахождения процентного соотношения или выражение частного в процентах.
(Методика работы над задачами подобной классификации будет рассмотрена ниже).
По характеру различают следующий вид задач:
1)На вычисление (это задачи, в которых необходимо выразить неизвестные величины (площади, отрезки, углы и т.д.) через известные, которые могут быть даны, как через числовые значениями, так и в общем виде),
2)На построение (это такие задачи для решения, которых необходимо построить геометрическую фигуру, удовлетворяющую условием задачи, при этом использовать можно только циркуль и линейку без деления),
3)На доказательство (эти задачи обладают определенной целью доказать, что то или иное утверждение верно или неверно, в заключение, должны получить окончательный ответ, в котором должно быть указано справедливость утверждения или его ошибочность),
4)На исследование (это задачи для решения, которых необходимо выбрать путь или средства для достижения определённой цели в соответствии с выделенной гипотезой),
5)На моделирование (это такие задачи, при решении которых необходимо выразить модель упрощённого подобия реального объекта, процесса или явления).
6)текстовые задачи,
7)задачи комбинированного характера.
Пример задачи на вычисление:
Среди людей 5% левшей и 9% людей, не подверженных морской болезни. В школе учится 1300 учащихся. Сколько среди них левшей и те которые не подверженны морской болезни?
Пример задачи на построение:
Построить с помощью транспортира угол в 120 градусов.
Пример задачи на доказательство:
Докажите, что сумма углов треугольника равна 180 градусов.
Пример задачи текстовой:
За 10 часов по течению реки теплоход «Паустовский» проходит тот же путь, что за 11 часов против течения. Найдите собственную скорость теплохода «Паустовский», если скорость течения реки 3 км/ч.
Пример задачи комбинированного характера:
Постройте треугольник по стороне и двум прилежащим углам и вычислите его площадь.
Г.В. Дорофеев делит задачи на два типа:
а) задачи, в которых описываются реальные жизненные ситуации;
б) задачи возможного характера, для которых жизненную ситуацию необходимо сконструировать, смоделировать, и выяснить условия, при которых она реализована.
Мы привели те классификации задач, с помощью которых учителю будет легче представить себе проблемы, которые связанны с методикой преподавания решению задач.
Классификация математических задач, классификация задач математического программирования
Виды математических задач, основанные на понятии стратегии обучения.
А.А. Столяр выделяет 3 вида задач.
1. Задача стандартная, способ решения которой знаком учащимся. Стратегия состоит в том, что мы обучаем распознаванию соответствующего вида задач и применению уже известного способа.
2. задача стандартная, но способ решения еще не знаком учащимся. Стратегия ориентируется на открытие учащимися способа решения таких задач: используются общие вопросы на этапе поиска решения, помогаем обнаружить учащимся способ, а на итогах просим составить алгоритм или схему решения.
3. Задача нестандартная. Стратегия ориентируется на обучение учащимися поиска способа решения ( Дж. Пойа «Как научиться решать задачу», Л. М. Фридман. Методы решения нестандартных задач).
Виды задач, основанные на понятии требования задач.
1. Задачи на нахождение искомого:
— задачи на вычисление,
— решение уравнений и неравенств,
— задачи, где требуется определить форму фигуры.
2. Задачи на доказательство или объяснение ( задачи со словами «доказать», «проверить», «ответить на вопрос почему?»).
3. Задачи на преобразование или построение.
Виды задач, основанные на понятии участвующие величины.
Задачи на движение, работу, на объем, стоимость, нахождение площади, задачи на проценты и т. д.
Виды задач, основанные на понятии полнота данных.
— Задачи с полным набором данных,
— задачи с недостающими данными,
— задачи с избыточными данными.
Отдельно выделяются задачи с противоречивыми данными. Например, решите задачу: из пункта А в пункт С. Из пункта В в С выезжают 2 велосипедиста, скорость первого 12 км/ч, скорость второго 15 км/ч. Когда второй прибыл в С первому оставалось ехать 12 км. Первый находился в точке Д отрезка АВ, что треугольник ВДС был равносторонним. Найдите расстояние между пунктом А и В, если треугольник АВС – прямоугольный (угол В=90).
Основания для подбора задач системы школьного курса математики.
Выделяют 2 основания:
1. Дидактическая цель, в соответствии с дидактической целью конструируется соответствующая система упражнений или задач.
Выделяют следующие цели.
— Подготовка к изучению теоретических вопросов математики (для актуализации знаний или для мотивации изучения).
— Усвоение новых знаний.
— Формирование умений и навыков (закрепление изученного, совершенствование опыта).
— Иллюстрация приложений.
— Повторение изученного.
— Контроль.
2. Способ деятельности. В соответствии с определенным способом деятельности выстраивается система упражнений. Способ деятельности может быть математическим (например, применение метода координат) и учебным (например, планирование своей деятельности).
При составлении той или иной системы упражнений желательно учитывать закономерности, которые могут привести к ошибочным действиям учащихся.
ВИДЫ ЗАДАЧ В МАТЕМАТИКЕ
|
Логические и математические задачи с собеседований
Разомнем мозг! В этой статье собраны логические и математические задачи, которые нередко встречаются на собеседованиях и могут попасться вам.
Основные проблемы, которые часто возникают в процессе интервью, не в отсутствии опыта или подготовки. Даже по-настоящему опытный разработчик может легко «споткнуться» о решение какой-нибудь хитро скроенной задачки. Поэтому мы поговорим не о том, как составлять резюме и выгодно презентовать себя. Фокусируемся на решении нетривиальных задач, которые включают в себя решение логического и/или математического характера.
Помните загадку из третьего фильма? Если нет, то вспоминайте, так как этим вопросом любят потчевать в Microsoft.
Задача:
Есть 2 пустых ведра: первое объемом 5 л, второе — 3 л. Как с их помощью отмерить 4 литра воды?
[spoiler title=’Ответ:’ collapse_link=’true’]Сперва наполните пятилитровое ведро. Далее перелейте из него воду в трехлитровое так, чтобы в пятилитровом осталось 2 л воды (полностью заполнив трехлитровое). Вылейте из меньшего ведра всю воду и перелейте в него оставшиеся в большем 2 л. Снова наполните пятилитровое и перелейте один литр в трехлитровое (оно как раз заполнится): так в большем ведре останется 4 л воды.[/spoiler]
Задача:
Есть двадцать баночек с таблетками. Почти во всех таблетки весят по 1 г, и только в одной — по 1,1 г. У нас есть точные весы, с помощью которых нужно определить баночку, каждая таблетка которой весит 1,1 г. Как это сделать, если можно взвесить только 1 раз?
[spoiler title=’Ответ:’ collapse_link=’true’]Давайте абстрагируемся и представим, что у нас 2 баночки, в одной из которых таблетки более тяжелые. Даже если мы поставим их обе на весы, мы ничего не узнаем. Но если мы достанем из одной баночки 1 таблетку, из другой — 2 и положим их на весы — вот тогда-то и откроется истина 🙂 В данном случае вес будет 2,1 или 2,2 (в зависимости от того, сколько каких таблеток мы взяли). Так и определяем нашу баночку.
Вернемся к задаче. Из каждой баночки нужно доставать разное количество таблеток. То есть из первой баночки 1 таблетку, из второй — 2, из третьей — 3 и так далее. Если бы каждая таблетка весила по 1 г, общий вес составил бы 210 г. Но поскольку в одной из баночек таблетки тяжелее, вес будет больше. Для определения нужной баночки просто воспользуемся формулой:
№ тяжелой баночки = (вес - 210) * 10[/spoiler]
Но на этом интересные логические и математические задачи не заканчиваются. Идем дальше!
Задача:
Парень и девушка договорились встретиться ровно в 21:00. Проблема в том, что у обоих часы идут неправильно. У девушки часы спешат на 2 мин., но она думает, что они на 3 мин. отстают. У парня же часы отстают на 3 мин., но он считает, что они на 2 мин. спешат. Кто из пары опоздает на свидание?
[spoiler title=’Ответ:’ collapse_link=’true’]Ничего сложного: чистая математика. Если у девушки часы спешат, а она думает, что они отстают, то поторопится и придет на 5 мин. раньше. Парень, наоборот, посчитает, что у него еще 5 минут времени в запасе, отчего на эти самые 5 мин. опоздает.[/spoiler]
Задача:
Длина курицы при измерении от головы до хвоста составит 45 см, а вот от хвоста до головы (если измерять вдоль брюха) — 53 см. По статистике плотность курицы на единицу боковой проекции составляет 8 г/см2. Усредненная высота курицы, если мерить ее вдоль боковой поверхности, — 21 см. Сколько весит килограмм курицы?
[spoiler title=’Ответ:’ collapse_link=’true’]Килограмм курицы весит 1 килограмм.[/spoiler]
Да, математические задачи с подвохом тоже встречаются 🙂
Задача:
Книга содержит N страниц, которые пронумерованы стандартно: от 1 до N. Если сложить количество цифр (не сами числа), что содержатся в каждом номере страницы, выйдет 1095. Так сколько в книге страниц?
[spoiler title=’Ответ:’ collapse_link=’true’]Каждый номер страницы имеет цифру на месте единицы, так что есть N цифр, расположенных на месте единицы. А вот после 9 начинаются двухзначные числа, и нам нужно добавить N-9 цифр. То же самое с трехзначными, которые начинаются после 99: добавляем N-99 цифр. Продолжать нет смысла, так как сумма не предполагает более 999 страниц. Получаем следующую формулу:
N + (N-9) + (N-99) = 1095
Далее просто решаем:
3N - 108 = 1095
3N = 1203
N = 401
Итого 401 страница.[/spoiler]
Задача:
Математические задачи на собеседованиях бывают и довольно простыми, но зачастую только на первый взгляд. Попробуйте в уме разделить 30 на 1/2 и прибавить 10. Каким будет результат?
[spoiler title=’Ответ:’ collapse_link=’true’]Первое решение, которое обычно приходит на ум, ошибочно:
30/2 + 10 = 25
Если мы делим на дробь, ее нужно переворачивать и производить умножение:
30*2 + 10 = 70[/spoiler]
Задача:
Сколько целых чисел в диапазоне 1-1000 вмещают в себя цифру 3? При подсчете нельзя пользоваться компьютером.
[spoiler title=’Ответ:’ collapse_link=’true’]Запомните, что нам нужно учесть просто факт содержания в числе тройки. Если, например, это 33 — мы не считаем цифру 2 раза. В числе должна быть по крайней мере одна тройка, чтобы его учесть. Например, числа в диапазоне 300-399 дают нам сразу 100 чисел. Еще 10 мы получаем от 30-39. То же касается 130-139, 230-239, etc. Десяток этих чисел уже был учтен при подсчете 330-339, так что убираем его и получаем:
100 + 90 = 190
А еще есть группа чисел (их 100), которые заканчиваются на тройку: 2-993. Мы исключаем из нее такие 10 чисел, как 303, 313 … 393 (они учтены ранее). Получаем еще +90 чисел. У 1/10 из этих 90 на месте десяток также расположилась тройка: 33, 133 … 933. Убираем еще 9, оставляя 81 число. Дальше простая математика:
100 + 90 + 81 = 271
А вот более изящное решение данной задачи. Сперва мы считаем, сколько чисел не включает в себя тройку (на каждое из 3-х мест ставится 9 цифр, которые не тройки):
9 * 9 * 9 = 729
1000 - 729 = 271[/spoiler]
Ну что, размялись? Надеемся, вам понравились собранные логические и математические задачи. Если этого мало, можете заглянуть сюда + ниже вы найдете еще больше задач, специально подобранных Библиотекой программиста 🙂
Поиск высококачественных заданий по математике для начальных классов в Интернете
Интернет может быть отличным ресурсом для поиска заданий по математике на любом уровне познавательных способностей. В то время как учащиеся начальной школы нуждаются в ознакомлении с задачами на всех уровнях — как более низком, так и более высоком — следует делать упор на более высоких уровнях. Это означает, что нам нужны навыки для оценки того, что является когнитивным требованием, а что нет.
Чтобы определить качество онлайн-активности, мы с моими партнерами по исследованиям использовали Руководство по анализу задач (TAG) Маргарет Шван Смит и Мэри Кей Штайн 1998 года, которое состоит из четырех различных уровней когнитивных требований: запоминание, процедуры без связей, процедуры со связями, и занимаюсь математикой.
При запоминании нет необходимости в критическом мышлении, не делается никаких связей с пониманием того, почему ответ работает, и процедуры игнорируются. Этот тип задач может выглядеть как напоминание фактов. Процедуры без соединений являются алгоритмическими; учащиеся придумывают ответ, не связываясь с другими математическими концепциями, и от них не требуется объяснять свою работу. Проблемы, связанные с простыми процедурами, например, требующие добавления стандартного алгоритма США, подпадают под эту категорию.Запоминание и процедуры без связей — это задачи с низкой когнитивной нагрузкой, потому что они не требуют много размышлений.
Учителя часто представляют визуальные диаграммы или манипуляторы, такие как кубы Unifix или блоки с базой 10, для решения математических задач, которые являются процедурами со связями, которые позволяют ученикам подходить к проблеме с разных сторон. В этих задачах используются процедуры, такие как алгоритм частичного произведения для умножения, чтобы помочь учащимся понять, почему ответ работает, а не только знание того, как найти ответ.
Задачи самого высокого уровня, связанные с математикой, требуют неалгоритмического мышления, требуют самоконтроля и позволяют использовать несколько стратегий — на этом этапе студенты изучают математические концепции.
Процедуры со связями и выполнение математических задач являются задачами с высоким когнитивным спросом, поскольку учащимся необходимо устанавливать связи, анализировать информацию и делать выводы для их решения, согласно Смиту и Стейну.
Задачи по математике, которые нужно выбирать критически
Для того, чтобы ставить ученикам начальных классов проблемы на всех когнитивных уровнях, учителя должны критически относиться к доступным ресурсам.Следующие пункты нашего исследования помогли мне и моим коллегам оценить когнитивную потребность и качество онлайн-задач.
Возраст имеет значение. Уровень познавательной потребности может меняться в зависимости от возраста детей, для которых была создана проблема. Например, заполнение рабочего листа основных задач сложения одной цифры будет закодировано как запоминание для четвероклассника, который, как ожидается, запомнит их (тем более, если ученик рассчитывает время), но это будет считаться выполнением процедур без соединения для детских садов, которые только узнают, что значит сложить две части, чтобы сделать одно целое.
Если вы ищете задачи с высоким когнитивным спросом, ресурс, отвечающий любому из следующих критериев, можно рассматривать как процедуру со связями; чтобы классифицировать как занимающегося математикой, должно быть несколько способов решения задачи:
- Проблема обычно связана с манипуляциями (например, 10 кадров, блоки с основанием 10, числовые линии, числовые сетки).
- Есть указания, в которых учащимся предлагается объяснить, как они нашли ответ (с помощью моделей, слов или того и другого).
- Требуется высокий уровень критического мышления. Например, учащиеся решают, как решить проблему, которую можно решить более чем одним способом, устанавливать реальные связи с математикой или объяснять свое математическое мышление.
Оценивая математическое задание, учителя также должны оценивать любые изображения, сопровождающие его. Включено ли изображение исключительно в декоративных целях или оно играет функциональную роль в решении проблемы? Изображения с функциональными ролями включают циферблаты, 10 кадров и графики.Если у деятельности есть декоративный образ, это, скорее всего, задача с низким уровнем когнитивных требований; если у него есть функциональное изображение, гораздо больше шансов, что он будет закодирован на высоком уровне когнитивных требований. Хотя занятие может быть популярным из-за его декоративных, милых изображений, его внешняя привлекательность никак не связана с высоким уровнем когнитивных потребностей. Важно сосредоточиться на содержании, а не на искусстве.
Где найти интеллектуальные математические задания
У вас значительно больше шансов найти математические задания с высоким уровнем когнитивного спроса на веб-сайтах, ресурсы которых просматриваются перед публикацией, в отличие от таких сайтов, как Teachers Pay Teachers или Pinterest, где любой может публиковать сообщения.Следующие сайты публикуют рецензируемые ресурсы:
- Иллюстративная математика позволяет учителям искать задания на основе стандартов содержания по предметной области или классу для K – 12 (бесплатно).
- EngageNY — это набор программ обучения английскому языку по искусству и математике от дошкольного до 8-го класса, разработанный Департаментом образования штата Нью-Йорк. Здесь также есть учебные программы по математике для старших классов — алгебра I и II, геометрия, предварительное вычисление и выше (бесплатно).
- NRICH, управляемый Кембриджским университетом в Англии, предоставляет библиотеку ресурсов и документов с картированием учебных программ для учащихся от 3 до 18 лет (бесплатно).
- youcubed, основанный профессором математического образования Стэнфордского университета Джо Боулером, предоставляет высококачественные математические задания, которые можно искать по классам (K – 12) или по теме. Некоторые задачи были созданы исследователями, которые запускают youcubed, а другие взяты с различных сайтов, включая NRICH (бесплатно).
- Illuminations — это онлайн-ресурс, доступный через Национальный совет учителей математики (NCTM), который предоставляет материалы, основанные как на стандартах NCTM, так и на Общих государственных стандартах для классов от pre-K до 12.Для доступа требуется членство в NCTM (стоимость: от 49 до 139 долларов в год).
Что такое математика? | Живая наука
Математика — это наука, которая занимается логикой формы, количества и расположения. Математика окружает нас повсюду, во всем, что мы делаем. Это строительный материал для всего в нашей повседневной жизни, включая мобильные устройства, архитектуру (древнюю и современную), искусство, деньги, инженерное дело и даже спорт.
С самого начала записанной истории математические открытия были в авангарде каждого цивилизованного общества и использовались даже в самых примитивных культурах.Потребности в математике возникли на основе потребностей общества. Чем сложнее общество, тем сложнее математические потребности. Первобытным племенам требовалось немного больше, чем умение считать, но они также полагались на математику для расчета положения солнца и физики охоты.
История математики
Несколько цивилизаций — в Китае, Индии, Египте, Центральной Америке и Месопотамии — внесли свой вклад в математику, которую мы знаем сегодня. Шумеры были первыми, кто разработал систему счета.Математики разработали арифметику, которая включает в себя основные операции, умножение, дроби и квадратные корни. Система шумеров перешла через Аккадскую империю к вавилонянам около 300 г. до н. Э. Шестьсот лет спустя в Америке майя разработали сложные календарные системы и были опытными астрономами. Примерно в это же время была разработана концепция нуля.
По мере развития цивилизаций математики начали работать с геометрией, которая вычисляет площади и объемы для выполнения угловых измерений и имеет множество практических приложений.Геометрия используется во всем: от домашнего строительства до моды и дизайна интерьера.
Геометрия идет рука об руку с алгеброй, изобретенной в девятом веке персидским математиком Мухаммедом ибн-Мусой аль-Ховаризми. Он также разработал быстрые методы умножения и погружения чисел, которые известны как алгоритмы — искажение его имени.
Алгебра предложила цивилизациям способ делить наследство и распределять ресурсы. Изучение алгебры означало, что математики решали линейные уравнения и системы, а также квадратики и копались в положительных и отрицательных решениях.Математики в древности тоже начали интересоваться теорией чисел. У истоков построения формы теория чисел изучает фигуральные числа, характеризацию чисел и теоремы.
Математика и греки
Изучение математики в рамках ранних цивилизаций было строительным материалом для математики греков, которые разработали модель абстрактной математики через геометрию. Греция с ее невероятной архитектурой и сложной системой управления была образцом математических достижений до наших дней.Греческие математики были разделены на несколько школ:
- Ионическая школа , основанная Фалесом, которому часто приписывают первые дедуктивные доказательства и разработку пяти основных теорем плоской геометрии.
- Школа Пифагора , основанная Пифагором, который изучал пропорции, плоскую и твердотельную геометрию, а также теорию чисел.
- Элейская школа , в которую входил Зенон Элейский, известный своими четырьмя парадоксами.
- Школа софистов известна как высшее образование в развитых греческих городах.Софисты давали инструкции по публичным дебатам, используя абстрактные рассуждения.
- Платоническая школа , основанная Платоном, который поощрял исследования в области математики в среде, очень похожей на современный университет.
- Школа Евдокса , основанная Евдоксом, который разработал теорию пропорций и величин и произвел множество теорем в плоской геометрии
- Школа Аристотеля , также известная как Лицей, была основана Аристотелем и последовала за ней. Платоническая школа.
Помимо перечисленных выше греческих математиков, многие греки оставили неизгладимый след в истории математики. Архимед, Аполлоний, Диофант, Папп и Евклид пришли из этой эпохи. Чтобы лучше понять последовательность и то, как эти математики влияли друг на друга, посетите эту временную шкалу.
В это время математики начали работать с тригонометрией. Вычислительная природа тригонометрии требует измерения углов и вычисления тригонометрических функций, которые включают синус, косинус, тангенс и их обратные величины.Тригонометрия основана на синтетической геометрии, разработанной греческими математиками, такими как Евклид. Например, теорема Птолемея дает правила для хорд суммы и разности углов, которые соответствуют формулам суммы и разности для синусов и косинусов. В прошлых культурах тригонометрия применялась к астрономии и вычислению углов небесной сферы.
После падения Рима развитие математики взяли на себя арабы, а затем европейцы. Фибоначчи был одним из первых европейских математиков и прославился своими теориями по арифметике, алгебре и геометрии.Эпоха Возрождения привела к достижениям, которые включали десятичные дроби, логарифмы и проективную геометрию. Теория чисел была значительно расширена, а теории вероятностей и аналитическая геометрия открыли новую эру математики с расчетом на переднем крае.
Развитие математики
В 17 веке Исаак Ньютон и Готфрид Лейбниц независимо друг от друга разработали основы математического анализа. Развитие математического анализа прошло три периода: ожидание, развитие и упорядочение.На этапе ожидания математики пытались использовать методы, включающие бесконечные процессы, чтобы найти области под кривыми или максимизировать определенные качества. На стадии разработки Ньютон и Лейбниц объединили эти методы через производную и интеграл. Хотя их методы не всегда были логически правильными, математики в 18 веке начали этап ригоризации и смогли обосновать их и создать заключительный этап исчисления. Сегодня мы определяем производную и интеграл в терминах пределов.
В отличие от исчисления, которое представляет собой тип непрерывной математики, другие математики придерживаются более теоретического подхода. Дискретная математика — это раздел математики, который имеет дело с объектами, которые могут принимать только отдельные, отдельные значения. Дискретные объекты можно охарактеризовать целыми числами, тогда как непрерывные объекты требуют вещественных чисел. Дискретная математика — это математический язык информатики, поскольку он включает изучение алгоритмов. Сферы дискретной математики включают комбинаторику, теорию графов и теорию вычислений.
Люди часто задаются вопросом, чем сегодня служат релевантные математики. В современном мире математика, такая как прикладная математика, не только актуальна, но и крайне важна. Прикладная математика — это разделы математики, которые занимаются изучением физического, биологического или социологического мира. Идея прикладной математики заключается в создании группы методов, решающих научные задачи. Современные области прикладной математики включают математическую физику, математическую биологию, теорию управления, аэрокосмическую инженерию и математические финансы.Прикладная математика не только решает задачи, но также открывает новые проблемы или развивает новые инженерные дисциплины. Прикладным математикам требуется опыт во многих областях математики и естественных наук, физической интуиции, здравого смысла и сотрудничества. Обычный подход в прикладной математике — построить математическую модель явления, решить модель и разработать рекомендации по повышению производительности.
Хотя чистая математика не обязательно противоположна прикладной математике, ее движут абстрактные проблемы, а не проблемы реального мира.Многое из того, чем занимаются чистые математики, может иметь свои корни в конкретных физических проблемах, но более глубокое понимание этих явлений порождает проблемы и технические детали. Эти абстрактные проблемы и технические детали и есть то, что пытается решить чистая математика, и эти попытки привели к крупным открытиям для человечества, включая универсальную машину Тьюринга, теоретизированную Аланом Тьюрингом в 1937 году. Универсальная машина Тьюринга, которая зародилась как абстрактная идея, позже заложил основу для развития современного компьютера.Чистая математика абстрактна и теоретически основана, и поэтому не ограничена физическим миром.
По словам одного чистого математика, чистые математики доказывают теоремы, а прикладные математики строят теории. Чистое и прикладное не исключают друг друга, но они уходят корнями в разные области математики и решения задач. Хотя сложная математика, используемая в чистой и прикладной математике, находится за пределами понимания большинства средних американцев, решения, выработанные на основе этих процессов, повлияли на жизнь всех и улучшили ее.
.4 Оценивание для поддержки изучения математики | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
обычно путем подсчета количества вопросов, на которые даны правильные ответы, и сравнения баллов одного человека с баллами другого на основании их относительного процентильного ранга. Так называемые оценки с привязкой к норме уже много лет беспокоят педагогов. Несмотря на то, что высказывались различные критические замечания по поводу ссылок на нормы, основная проблема образования заключается в том, что такая информация недостаточно полезна для улучшения обучения и обучения и может, фактически, иметь контрпродуктивные образовательные последствия.В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут использоваться вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.
Программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и что они думают о математике. |
Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, что будет преподаваться. Таким образом, программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и что они думают о математике. Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания учащимся, а не только баллов вне контекста.
Чтобы обучение было эффективным, результаты оценки должны быть своевременными. 35 Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после того, как классы заканчиваются в течение года и учащиеся ушли, ни учителя, которые уделяют слишком много времени выставлению оценок. В частности, необходимо найти новые способы, чтобы дать учителям и ученикам более непосредственные знания об успеваемости учеников по оценкам, предписанным внешними властями, чтобы эти оценки, а также собственные оценки учителя могли использоваться для улучшения обучения.Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять учащимся и учителям отчеты об их успеваемости. Школьное время дорого. Когда учащимся не сообщают об их ошибках и заблуждениях, не говоря уже о том, чтобы помочь их исправить, оценка может как усилить недопонимание, так и потратить драгоценное учебное время впустую.
Когда форма оценивания незнакома, учителя несут особую ответственность перед своими учениками, чтобы сообщить им заранее.
.6 Оценка аттестата по математике | Измерение того, что имеет значение: концептуальное руководство для оценки по математике
П OSTSCRIPT
Три предложенных здесь принципа — содержание, обучение и равенство — функционируют как гироскоп для реформы математического оценивания, который поможет продолжить реформу математики и привести к новым оценкам, которые отражают важную математику, поддерживают хорошее обучение и продвигают возможности каждого учащегося. учиться.
Система наведения этого гироскопа является мощным инструментом на пути к реформе системы оценивания. Однако это всего лишь инструмент, сам по себе недостаточный для решения поставленной задачи. Не менее важны пригодность судна для рейса, экипаж, способный внести необходимые поправки на середине курса, и подробная навигационная карта, показывающая желаемый порт.
Сосудом реформы является общенациональный акцент на системных изменениях: скоординированный ответ всех основных компонентов образовательной системы (учебная программа, преподавание, оценка, управление, педагогическое образование, школьная организация и т. Д.)). По математике судно особенно прочно и хорошо спущено на воду. Уже доступны описания задачи (Все на счету), цели того, что студенты должны изучать (Учебный план и стандарты оценки), и методы обучения, необходимые для поддержки этого обучения (Профессиональные стандарты преподавания математики). NCTM сейчас разрабатывает третий из серии томов стандартов, на этот раз по оценке. В этом томе, который планируется выпустить весной 1995 года, будут изложены стандарты оценивания, которые служат целому ряду целей — от обучения в классе до политики, оценки программ, планирования и распределения студентов.Три компонента стандартов — учебная программа, педагогика и оценивание — обеспечивают основу для обновления педагогического образования, переосмысления школьной организации, активизации реализации реформ и содействия диалогу о системных изменениях между многими заинтересованными сторонами в математическом образовании.
Резервы на рейс обеспечиваются материальными ресурсами, что стимулирует широкое участие в реформе оценивания. Эти ресурсы предоставляют богатый набор примеров высококачественного оценивания, созвучного видению математики и математического образования, выраженному в Стандартах .Некоторые из них предоставляют конкретные примеры, иллюстрирующие всеобъемлющие идеи (например, Mathematics Assess —
.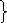 I п. — 5 кн.
I п. — 5 кн.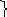 Iп. — 5 кн.
Iп. — 5 кн.