Урок 38. решение задач. часть 2. — Математика — 2 класс
Математика, 2 класс
Урок № 38. Решение задач
Перечень вопросов, рассматриваемых в теме:
— решение текстовых задач арифметическим способом, представление текста задачи в виде модели.
Глоссарий по теме:
Задача — упражнение, которое выполняется посредством умозаключения, вычисления.
Простая задача — задача, которая решается при помощи одного действия.
Составная задача — задача, в решении которой используют два или более действий.
Основная и дополнительная литература по теме урока:
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.17.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций.
Теоретический материал для самостоятельного изучения
Приступая к решению любой задачи, необходимо знать её составные части.
Части задачи: условие, вопрос, решение, ответ.
Давайте выясним, который текст будет являться задачей.
Первый текст:
Дети нашли 9 грибов. Игорь нашёл 7 грибов, а Миша 2 гриба.
Второй текст:
Игорь нашёл 7 грибов, а Миша 2 гриба. Сколько грибов нашли дети?
Мы уже знаем, что в задаче должны быть обязательно условие и вопрос.
Разберемся, какие составные части можно выделить в этих текстах.
Первый текст: дети нашли 9 грибов. Игорь нашёл 7 грибов, а Миша 2 гриба-не содержит вопроса. Значит, он не может быть задачей.
Второй текст:
Игорь нашёл 7 грибов, а Миша 2 гриба. Сколько грибов нашли дети? -состоит из двух частей.
Игорь нашёл 7 грибов, а Миша 2 гриба — это условие нашей задачи.
Сколько всего грибов нашли дети?- это вопрос задачи.
Условие и вопрос задачи можно представить в виде схемы. Для этого изобразим грибы, которые находили дети, отрезками.
Игорь — 7 грибов, Миша — 2 гриба
М. 2 гр
В вопросе спрашивалось, сколько всего грибов нашли дети. Слово «всего» мы передадим в схеме при помощи фигурной скобки. Поставим знак вопроса.
И. 7гр
М. 2 гр ?
Решим эту задачу. Рассуждаем: в задаче неизвестно целое, поэтому для нахождения целого мы выполним действие сложения.
7 + 2 = 9 (гр.)
Мы узнали, что дети нашли 9 грибов. Теперь необходимо записать ответ. Вопрос был: «Сколько всего грибов нашли дети?»
Ответ: 9 грибов.
После решения проверим, все ли элементы записаны. Мы записали краткое условие и вопрос в виде схемы, решение задачи и ответ.
Сделаем вывод.
Чтобы решить задачу, нужно:
1) Прочитать ее условие.
2) Подумать, с помощью какого действия вы ответите на вопрос задачи.
3) Решить задачу по действиям или выражением.
4) Правильно записать ответ.
Тренировочные задания.
1. Решите задачу: В корзине лежало 36 лимонов. Продали 20 лимонов. Сколько лимонов осталось?
Правильный ответ: 36 — 20 = 16 (л)
2. Решите задачу: С одной берёзы упало 10 листиков, а с другой 7 листиков. Сколько всего листиков упало с двух берёз?
Правильный ответ: 10 + 7 = 17 (л)
| 1. |
Запиши выражение и найди его значение (вычитание и сложение)
Сложность: лёгкое |
2 |
2.
|
Запиши выражение и найди его значение (два вычитания)
Сложность: лёгкое |
|
| 3. |
Сравни выражения
Сложность: лёгкое |
1 |
4.
|
Найди общее количество человек в двух автобусах
Сложность: среднее | 2 |
| 5. |
Количество шаров
Сложность: среднее |
|
6.
|
Сколько французских монет?
Сложность: среднее | 2 |
| 7. |
Число карасей
Сложность: среднее |
2 |
8.
|
Хватит ли денег на покупку?
Сложность: сложное | 3 |
| 9. |
Число перин у госпожи Метелицы
Сложность: сложное |
3 |
10.
|
Количество бензина в баке
Сложность: сложное |
3 |
| 11. |
Выбери правильный ответ
Сложность: сложное |
3 |
ГДЗ по Математике 2 класс Моро, Бантова учебник Решебник
Здесь представлен учебник по математике для самых маленьких школьников (2 класс) с готовыми ответами и правильными алгоритмами решения. Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Авторами выступили известные методисты М.И. Моро, М.А. Бантова, Г.В. Бельтюкова, С.И. Волкова и С.В. Степанова. Готовые домашние задания (ГДЗ) облегчают задачу вхождения в учебный процесс и помогают быстрее приступить к конструктивному познанию основ этого важного и занимательного предмета. Изданием учебно-методического комплекса является «Школа России». На нашем сайте представлены только актуальные задания из указанного источника и правильные ответы к ним.
Почему решебник по математике Моро нужен каждому второкласснику?
ГДЗ помогают ребенку мотивировать себя, чтобы заниматься самостоятельно, а также постоянно контролировать достигнутый уровень личного прогресса посредством решения проверочных упражнений. Со сборником по математике Моро, Бантовой, Бельтюковой, который полностью соответствуют ФГОС и повсеместно используются в рабочих программах педагогов, легко и удобно заниматься. Верные ответы онлайн имеют следующие преимущества перед иными видами пособий:
- наличие независимых вариантов выполнения многих примеров;
- примеры снабжены ценными методическими указаниями;
- сайт работает с персонального компьютера, ноутбука, планшета и смартфона;
- таблица номерных указателей позволяет быстро находить нужное задание.

С онлайн-решебником можно успешно готовиться к контрольным, проверочным, самостоятельным, и диагностическим работам, выполнять тесты и проходить внешнее независимое тестирование в конце учебного года.
Чем ГДЗ Моро, Бантовой превосходит другие учебники для 2 класса?
Чтобы хорошо успевать по математике и приносить домой исключительно отличные отметки, нужно приучить себя к систематической и тщательной работе. Это касается как отработки устного счета, так и формирования четкого понимания способов решения задач на одно и два действия. Во втором классе общеобразовательной школы ученики знакомятся лишь с самыми простыми понятия, но именно они станут залогом будущих успехов при изучении точных дисциплин. Ни в коем случае нельзя запускать предмет, а возникающие пробелы в знаниях, умениях и навыках необходимо ликвидировать в кратчайшие сроки. Сборник способен оказать значительную помощь в достижении следующих целей:
- повышение текущей успеваемости и степени уверенности в собственных силах на уроках;
- отработка практических навыков в области арифметики;
- формирование самостоятельности при подготовке к урокам;
- расширение кругозора и формирования навыков логического мышления.

Математика относится к тем предметам, которые непременно пригодятся будущему взрослому члену общества. Уметь произвести те или иные практически важные и полезные вычисления необходимо повсеместно. Поэтому пособие Моро для 2 класса рекомендовано наиболее широким массам учащихся, а также их неравнодушным родителям, которые хотели бы держать под контролем учебный прогресс своего сына или дочери.
Задачи для 1 — 2 класса
Примеры решения задач по математике
Задача №1
В шкафу стояло 39 книг. Когда на полку переставили несколько книжек, их там осталось 25.
Сколько книг переставили на полку?Решение:
39 — 25 = 14 (кн.)Ответ: на полку переставили 14 книг.
Задача №2
Когда со стоянки уехало 4 машины, там осталось ещё 26.
Сколько машин было на стоянке?Решение:
26 + 4 = 30 (маш.)
Ответ: на стоянке было 30 машин.
Задача №3
У Олега было 15 почтовых марок. 5 марок он использовал.
Сколько марок осталось у Олега?Решение:
15 — 5 = 10 (мар.)Ответ: у Олега осталось 10 марок.
Задача №4
На элеватор привезли 45 т ржи, а пшеницы 15 т.
Сколько всего зерна привезли на элеватор?Решение:
45 + 15 = 60 (т)Ответ: на элеватор привезли 60 тонн зерна.
Задача №5
Петя собрал по теме «Космос» 25 марок, а по теме «Флот» только 9.
Сколько всего марок в Петиной коллекции?Решение:
25 + 9 = 31 (мар.)Ответ: в Петиной коллекции 31 марка.
Задача №6
В ларёк привезли 15 ящиков яблок и 8 ящиков слив.
Сколько всего привезли ящиков с фруктами?Решение:
15 + 8 = 23 (ящ.)Ответ: в ларёк привезли 23 ящика с фруктами.
Задача №7
Бабушка посадила 16 кустиков клубники, а внучка 5.
Сколько всего кустиков клубники они посадили?Решение:
16 + 5 = 21 (кус.)Ответ: они посадили 21 куст клубники.
Задача №8
В школьную столовую привезли 15 кг картофеля, через 2 дня ещё 10 кг.
Сколько всего килограммов картофеля привезли?Решение:
15 + 10 = 25 (кг)Ответ: всего привезли 25 кг картофеля.
Задача №9
На стройку привезли 5 ящиков больших гвоздей и 8 ящиков маленьких.

Сколько всего привезли ящиков с гвоздями?Решение:
5 + 8 = 13 (ящ.)Ответ: на стройку привезли 13 ящиков с гвоздями.
Задача №10
Дедушка налил в бочку 18 вёдер воды и привёз в сад. Из бочки, под кусты, вылили 7 вёдер воды.
Сколько вёдер воды осталось бочке?Решение:
18 — 7 = 11 (вёд.)Ответ: в бочке осталось 11 вёдер воды.
Домашнее задание
Чтобы легко и быстро решать аналогичные задачи нужно закрепить знания выполнив несколько заданий самостоятельно. Реши задачу и дай ответ.
Пример 1
На праздник 9 Мая дети читали стихи. Девочки прочитали 7 стихов, а мальчики 9. Сколько всего прочитали стихотворений?
Пример 2
Оля помогала маме мыть посуду.
Мама помыла 6 тарелок, а Оля помыла 3 чашки. Сколько всего вымыто посуды?
Пример 3
К новогоднему празднику ученики украсили школьный класс. Девочки вырезали из бумаги 15 снежинок, а мальчики 20 хлопушек. Сколько всего украшений сделали ученики?
Пример 4
В классе на подоконниках окнон стоят 36 горшков с цветками. На первом подоконнике стоят 12 горшков, на втором 14. Сколько горшков на третьем подоконнике?
Пример 5
У Коли в аквариуме 18 рыбок – 9 скалярий и 11 барбусов. Коля подарил Ване 4 скалярия, а Пете 4 барбуса. Сколько рыбок каждой породы осталось у Коли?
Если заметили ошибку, выделите фрагмент текста и нажмите Ctrl+Enter
ГДЗ по математике 2 класс Моро учебник
ГДЗ по математике – залог успеха второклассника!
Второклассникам приходится считать много и постоянно! Еще бы, ведь содержание курса математики включает в себя не только сухие примеры. В теме «Рубль. Копейка» ребятам предстоит считать деньги. В темах, посвященных нумерации, они переводят метры в миллиметры. Часам и секундам тоже нашлась специальная тема. А ведь при этом приходится еще делать вычисления с переходом за десяток, учиться выполнять действия в скобках, разбираться, откуда в уравнениях взялись буквы и что они обозначают, выполнять множество других заданий. Задача учителя и родителей – сформировать прочные навыки выполнения арифметических действий, без которых невозможно успешное изучение большинства школьных наук. Для поиска требуемого задания или упражнения по математике для второго класса необходимо выбрать соответствующую часть: первую или вторую, найти искомый номер страницы из учебника, перейти по ссылке на страницу с решением и найти искомый ответ на номер своего примера или задачи.
В теме «Рубль. Копейка» ребятам предстоит считать деньги. В темах, посвященных нумерации, они переводят метры в миллиметры. Часам и секундам тоже нашлась специальная тема. А ведь при этом приходится еще делать вычисления с переходом за десяток, учиться выполнять действия в скобках, разбираться, откуда в уравнениях взялись буквы и что они обозначают, выполнять множество других заданий. Задача учителя и родителей – сформировать прочные навыки выполнения арифметических действий, без которых невозможно успешное изучение большинства школьных наук. Для поиска требуемого задания или упражнения по математике для второго класса необходимо выбрать соответствующую часть: первую или вторую, найти искомый номер страницы из учебника, перейти по ссылке на страницу с решением и найти искомый ответ на номер своего примера или задачи.
Учебник часть 1 (страницы)
4567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495Учебник часть 2 (страницы)
456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111Смотреть ГДЗ к рабочей тетради по математике за 2 класс Моро
Почему второкласснику трудно дается математика
Школьник тоже осознает необходимость серьезного отношения к важному предмету. И очень хочет, чтобы у него все получалось. Но путь к желанному результату для многих детей оказывается довольно сложным.
И очень хочет, чтобы у него все получалось. Но путь к желанному результату для многих детей оказывается довольно сложным.
Не все ребята сформировали навыки абстрактного мышления, не каждый в дошкольном детстве подготовил свою память и внимание к усвоению большого количества информации.
Родители могут помочь ребенку. Ведь они, как никто другой, заинтересованы в успехах собственного чада. Но мамы и папы не знают современных подходов к обучению в младшей школе, им неизвестны требования к оформлению практических работ разного вида.
ГДЗ поможет всем!
Проблему снимает обращение к дополнительному образовательному ресурсу – готовым заданиям по математике, специально составленным к учебнику М.И.Моро.
Здесь собраны все те работы, которые включены в 1 и 2 части учебного пособия. Но если в учебнике они представлены в виде пособий, то в решебнике под каждым номером содержится правильный ответ, подробное решение, грамотное оформление работы.
Теперь при любом затруднении ученика он сможет увидеть, как работать со схемой или рисунком, как решить уравнение и задачу, как представить ответ в виде чертежа и дать к нему объяснения. Наглядный пример очень важен для детей, у которых еще не полностью сформировано абстрактное мышление.
Наглядный пример очень важен для детей, у которых еще не полностью сформировано абстрактное мышление.
Взрослые тоже не могут обойтись без ГДЗ. Если малыш не разберется в задаче самостоятельно, он придет к маме. Ей понадобится пара минут, чтобы с помощью решебника понять логику поиска ответа.
Педагог, вооружив родителей готовыми домашними заданиями, получает армию консультантов, которые восполнят нехватку времени на уроке.
ГДЗ по математике – залог успеха второклассника!
Математика 2 класс: учебники, решебники, примеры
Математика 2 классПравила и упражнения по математике для 2 класса0
Главный герой математической серии «Мудрая Сова» предлагает второклассникам дружбу и сотрудничество. Задания, которые школьник найдет на страницах тетради
Математика 2 класс3000 примеров по математике для 2 класса. Табличное умножение и деление0
Три тысячи примеров от практикующего педагога Узоровой О. помогут второклассникам выучить математику «на отлично». Всевозможные случаи деления и умножения
Математика 2 классТренажер по математике для 2 класса0
Тренажеры по математике рекомендованы тем учителям и родителям, которые понимают важность быстрого счета для успешного усвоения математическими навыками.
Математика 2 классСамостоятельные и контрольные работы по математике для 2 класса к учебнику Петерсон Л.Г.0
Контрольные и предшествующие им самостоятельные работы направлены на подготовку второклассника к серьезному испытанию – итоговому уроку.
Математика 2 классРабочая тетрадь по математике для 2 класса к учебнику Моро М.И.0
Тетради с печатной основой входят в комплект к учебным сборникам Моро для второго класса. Они значительно повышают насыщенность и продуктивность урока.
Они значительно повышают насыщенность и продуктивность урока.
0
В математике, как и в любой другой точной науке, важное значение имеют интенсивные дополнительные занятия. Они позволяют довести важнейшие математические
Математика 2 классКарточки по математике для 2 класса0
Индивидуальная работа на уроках математики позволяет педагогу дать ученикам именно ту нагрузку, в которой они нуждаются. Таким образом, с помощью индивидуальных
Математика 2 классСборник задач по математике для 2 класса0
Планируя урок, для решения всевозможных задач учитель отводит половину урочного времени. Задачи – это прекрасный способ связать и конкретизировать математические
Математика 2 классУпражнения по математике для 2 класса0
Для полноценного усвоения математических приемов счета и терминологии, второклассникам необходимо постоянно упражняться. Ведь ничто так не способствует
Математика 2 классОлимпиада по математике для 2 класса. Кенгуру – 2013. Задания и ответы0
«Кенгуру» – большая международная олимпиада по математике. В ней могут участвовать все школьники, начиная со второго класса. Олимпиадные задания предыдущих
Математика 2 классСборник тестов по математике для 2 класса0
Математические задания-тесты, предлагаемые в данном сборнике, рекомендованы для диагностики знаний на проверочных уроках, для самопроверки и индивидуальных работ.
Математика 2 классЗадачи по математике для 2 класса на умножение и деление0
Задачи во втором классе становятся заметно сложнее. Каждый этап в обучении для ученика начальной школы значителен. И если в знаниях ребенка допущен пробел
Каждый этап в обучении для ученика начальной школы значителен. И если в знаниях ребенка допущен пробел
0
Логика – верная спутница математики и наука, совсем недавно получившая отдельные часы в школьной программе (как правило, факультативы).
Математика 2 классЗадания по математике для 2 класса0
Все вопросы, связанные с закреплением математических знаний решаются с помощью дополнительных заданий. Ведь многие математические правила, логические понятия
Математика 2 классЗадачи для 2 класса по математике в 2 действия0
Начальный и основной этап подготовки к решению самых разнообразных задач в средней школе дети проходят в первом-четвертом классах. Это значит, что школьники
Математика 2 классЛогические задачи для 2 класса0
Логика, как самостоятельный предмет пришла в школы совсем недавно. Поэтому качественная учебная литература, направленная на развитие мыслительных операций
Математика 2 классОлимпиадные задания по математике для 2 класса0
Для детей, развитие которых превышает стандартный уровень, государственные образовательные структуры проводят математические конкурсы (олимпиады разных уровней).
Математика 2 классЗанимательная математика для 2 класса0
Веселые логико-математические задания для второклассников относятся к разновидности дополнительных математических материалов. Не смотря на то, что многие
Математика 2 класс3000 примеров по математике для 2 класса. Узорова О.В. Нефедова Е.А.0
Определяющим показателем навыков счета методисты называют скорость, с которой дети решают пример. Сборники заданий для 2 класса, направленных на автоматизацию
Сборники заданий для 2 класса, направленных на автоматизацию
0
Серия индивидуальных математических учебников от Узоровой О. и Нефедовой Н. предлагает сборники практических заданий для учеников вторых классов.
Математика 2 классРешебник по математике для 2 класса к учебнику Петерсон Л.Г.0
Обучение во втором классе усложняется новыми приемами счета, как письменного, так и устного. Задача взрослых – контролировать качество усвоения материала
Математика 2 классРешебник по математике для 2 класса к учебнику Моро М.И.0
Основная задача такого пособия, как решебник, — контроль знаний и определение недостатков в системе ЗУН ученика. Так как сейчас педагоги имеют право выбирать
Математика 2 классУчебник по математике для 2 класса. Моро М.И.
Моро М.И.0
Учебники Моро М.И. принадлежат к самым востребованным обучающим пособиям для второклассников. Книга, составленная коллективом педагогов-практиков и опытных
Математика 2 классУчебник по математике для 2 класса. Петерсон Л.Г.0
Учебник – это главное средство обучения, как на уроках, так и дома. Поэтому важно, чтобы учитель любил и понимал программу того автора, которого он выбрал
Математика. 2 класс
Задачи:
1. Развитие умений решать задачи и составлять обратные, сравнивать величины, находить неизвестный множитель, познакомить с таблицей умножения на два.
2. Развитие логического мышления, внимания, памяти.
3. Воспитание интереса к математике, стремление использовать математические знания в повседневной жизни.
4. Повышение интереса к изучению ПДД через проведение интегрированного урока.
5. Повторение дорожных знаков.
Оборудование: стенды модульного кабинета ПДД, дорожные знаки, карточки, магнитофон.
Ход урока
1. ОРГМОМЕНТ
Приветствие, знакомство учащихся с целями и задачами урока.
2. СООБЩЕНИЕ ТЕМЫ
— Сегодня на уроке математики мы будем работать над таблицей умножения на два, решать и составлять обратные задачи, решать уравнения, находить сторону квадрата по известному периметру, а также повторим дорожные знаки, вспомним, что они обозначают.
(Класс сидит по группам.)
— Группы наши превращаются в экипажи машин дорожно-патрульной службы, а командиры будут штурманами. Штурман — это человек, который руководит всем движением.
Двигаться мы будем по городу. Городские дороги — это ваши тетради, в которых вы должны писать красиво, грамотно и аккуратно.
Откройте тетради, запишите дату.
Сядьте правильно, пристегнитесь ремнём безопасности.
Как вы думаете, зачем это необходимо сделать?
(Дети отвечают, поднимая руку. Добившись полного, правильного ответа, продолжаем.)
— Итак, мы отправляемся в путь! Будьте внимательны! Поехали!
3. УСТНАЯ РАБОТА
— Поехали и вдруг видим: на проезжей части дороги стоит человек. Кто это? Отгадайте?
(Учитель читает стихотворение.)
Кто-то запросто-непросто
Встал на нашем перекрёстке!
Быстро руку протянул,
Ловко палочкой взмахнул.
Вы видали?
Вы видали?
Все машины сразу встали!
Дружно встали в три ряда
И не едут никуда.
Ребята, кого мы увидели?
(Инспектора ГИБДД.)
Откройте конверт № 1.
(В конверте вопрос: «Как называется предмет, которым регулировщик управляет движением?».)
Для ответа слушайте задание. Вам надо решить выражения и значения расположить в порядке возрастания.
Вам надо решить выражения и значения расположить в порядке возрастания.
Какое слово у вас получилось? (Жезл.)
Задание в конверте:
83-67=15 (Е)
52-44=8 (Ж)
36+29=65 (З)
72+28=100 (Л)
Давайте вспомним, что обозначают сигналы регулировщика?
(Дети отвечают: если он стоит лицом или спиной с опущенными или вытянутыми в сторону руками — движение для транспорта и пешеходов запрещено. Если правая рука вытянута вперёд — путь пешеходам открыт за спиной регулировщика. Если рука поднята вверх — внимание! Движение всех запрещено!)
Справились! Молодцы!
(Регулировщик показывает: путь открыт. Едем дальше.)
Ребята, что за знак впереди? («Жилая зона».)
Как надо ехать? Почему? (Ответы детей: медленно, осторожно.)
Смотрите! На проезжую часть выбежал футболист. Найдите, под каким номером этот футболист. (Карточка № 1, в которой изображены геометрические фигуры. )
)
Как вы думаете, правильно ли поступил мальчик?
Почему?
А вы, водители, поступаете правильно? Молодцы!
4. РАБОТА НАД НОВЫМ МАТЕРИАЛОМ
Решение выражений
— Чтобы с вами не произошло таких историй, мы сейчас повторим знаки дорожного движения. Будьте внимательны! (Учитель показывает дорожные знаки, на которых записаны выражения. Дети пишут в тетрадях эти выражения и находят их значения.)
2*2= 3*2= 4*2=
5*2= 6*2= 7*2= 8*2=
Что обозначает этот знак?
Хорошо, вы вспомнили знаки, а сейчас включим музыку и постараемся запомнить слова, которые услышим в песне.
(Звучит песня «Таблица умножения».)
— Ребята, какие знаки вы знаете?
Что обозначает этот знак? (Звуковой сигнал запрещён.)
Геометрический материал
— Как называются геометрические фигуры, форму которых имеют знаки? (Треугольник, квадрат, круг, прямоугольник.)
Почему они разные?
(Знаки принадлежат к разным группам: предупреждающие, запрещающие, предписывающие, знаки приоритета, сервиса, информационо-указательные, знаки особых предписаний. )
)
— Назовите разрешающий знак, в котором есть буква?
Что это за буква? (Р)
Что обозначает этот знак? (Место стоянки.)
А в математике что обозначает эта буква? (Периметр.)
Нахождение периметра
— Что называется периметром?
Как найти периметр?
В какой геометрической фигуре находится эта буква? (В квадрате.)
Что вы знаете о квадрате?
Как найти периметр квадрата?
Откройте конверт № 2.
Найдите периметр квадрата.
Если дан периметр квадрата, как найти его сторону?
Запишите в тетрадях эту задачу. Чей экипаж справится с заданием, штурман поднимет руку.
Р=2+2+2+2 Р=8 см
а=8 см а=2 см
Устали? Поехали на парковку. Вышли из машин.
Физминутка.
Решение задач
— На этом стенде находятся машинки. Сосчитайте их и составьте условие задачи, которая решалась бы умножением.
(3*2= 6 машин. )
)
— Составьте обратные задачи (6:3=2; 6:2=3), запишите их в тетрадях.
Закончили? Садимся в машины.
К какому виду транспорта относятся ваши машины? (Специальный.)
Как передвигается спецтранспорт? (Едет с включённым звуковым сигналом, ему должны уступить дорогу даже на красный свет.)
Решение уравнений
Читает ученик:
— Эй, водитель, осторожно!
Ехать быстро невозможно,
Знают люди все на свете:
В этом месте ходят… дети.
Учитель:
— Найдите этот знак. Где его можно встретить?
(Дети отвечают: знак устанавливается около школ и предупреждает водителей, что в этом месте могут появиться на дороге дети. Но этот знак не разрешает переходить дорогу в том месте, где он установлен. Для перехода нужно поискать пешеходный переход, который обозначается знаком — синим квадратом с нарисованным внутри человечком.)
Учитель:
— Нашли карточку с легковой машинкой в круге с красным ободом?
Что означает этот знак?
(Дети отвечают. )
)
Как называются компоненты при умножении?
Как найти неизвестный множитель?
Решите уравнение, сделайте проверку. (а*9=18)
Сравнение выражений
— Отгадайте загадку:
Этот конь не ест овса,
Вместо ног — два колеса,
Сядь верхом и мчись на нём,
Только лучше правь рулём. (Велосипед.)
Кто знает, в каком году изобрели велосипед? Кто изобрёл?
(Первый прототип велосипеда был предложен великим итальянским учёным Леонардо да Винчи в 1495 году: показать иллюстрации.)
У кого из вас есть велосипед?
Какие правила для велосипедистов вы знаете?
Покажите предписывающий знак для велосипедиста.
И запрещающий. В чём их различие? (Дети отвечают устно.)
Выполним следующее задание. Сравните величины.
Вспомните, сколько сантиметров в 1 дециметре? А сколько миллиметров в 1 сантиметре?
(Дети записывают ответы в тетрадях. )
)
Чей экипаж справился с этим заданием? Молодцы!
5. ДОМАШНЕЕ ЗАДАНИЕ
Придумать разрешающий знак.
6. ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП УРОКА
Самый дружный, самый быстрый экипаж — это… (учитель называет лучшую группу). Молодцы!
Что нового узнали на уроке? Что запомнили?
Послушайте стихотворение
Читает ученик:
Правил дорожных
На свете немало,
Все бы их выучить
Нам не мешало,
Но основное из правил движения
Знать как таблицу
Должны умножения.
На проезжей части не шалить,
Не играть,
Не кататься,
Если хочешь целым быть
И живым остаться!
Учитель начальных классов, отличник народного просвещения Л.В. ШАШКОВА, МОУ Средняя общеобразовательная школа № 32, г. Красноярск
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать. Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер.Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
- Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.
 Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути. - Завершите: Просканируйте текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблем.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Рабочих листов всего три, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и научиться словесным методам решения проблем в расслабленном темпе. В печатных материалах содержатся термины, которые будут знакомы молодым учащимся, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: если вы вычеркнете слова, это будут простые задачи на сложение и умножение, где ответ на первый вопрос будет следующим: 12 робинов + 7 робинов = 19 робинов; а ответ на второй: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. РасселЭта последняя распечатка из набора содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если ученики не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда проблема превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если ученики не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда проблема превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Реальный мир Решение задач по математике для второго класса
Edgewood Magnet School в Нью-Хейвене, штат Коннектикут, — это школа-магнит, которая объединяет искусство в учебную программу. Студентам в этой среде рекомендуется использовать стратегии наблюдения, интерпретации и анализа, чтобы улучшить свои навыки мышления по каждому предмету. С этой миссией и учителя, и ученики используют уникальные и захватывающие подходы к «основам» и работают вместе, чтобы обеспечить включение всех учащихся.
Для большинства второклассников начало года — время освежить знания и навыки первого класса. Лето вдали от прямого обучения и возможностей для практики и руководства иногда означает потерю твердого понимания изученных концепций математики. Этот трех-четырехнедельный блок предназначен для обзора и формирования нового понимания одноэтапного решения словесных задач с использованием сложения и вычитания по мере того, как учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года.Учащиеся с помощью серии математических сценариев будут использовать типы задач, указанные в Таблице 1 Общего базового математического глоссария, который охватывает сложение и вычитание. 1
Этот трех-четырехнедельный блок предназначен для обзора и формирования нового понимания одноэтапного решения словесных задач с использованием сложения и вычитания по мере того, как учащиеся развивают навыки и стратегии, которые они будут использовать в течение всего года.Учащиеся с помощью серии математических сценариев будут использовать типы задач, указанные в Таблице 1 Общего базового математического глоссария, который охватывает сложение и вычитание. 1
Common Core концентрируется на четком наборе математических навыков и концепций. Учащиеся изучают концепции организованным образом в течение учебного года, а также в разных классах. Стандарты побуждают студентов решать реальные проблемы. 2
Common Core требует больше внимания к математике.Вместо того, чтобы стремиться охватить множество тем в учебной программе шириной в милю и глубиной в дюйм, стандарты просят учителей математики значительно сузить и углубить то, как время и энергия тратятся в классе. Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает концепции, навыки и решение проблем, связанных с сложением и вычитанием.
Это означает четкое сосредоточение внимания на основной работе каждого класса, которая для классов от детского сада до второго класса включает концепции, навыки и решение проблем, связанных с сложением и вычитанием.
В округе государственных школ Нью-Хейвена используется сингапурский подход Math in Focus, — учебная программа на основе Common Core для учащихся от детского сада до пятого класса.Учебники и рабочие тетради для учащихся следуют учебному плану, который включает изучение концепций и навыков посредством наглядных уроков и инструкций учителя для понимания того, как и почему; объединение концепций и навыков посредством практики, занятий и математических журналов для глубокого понимания математики, практической работы в парах и в небольших группах; и, , применение концепций и навыков посредством обширной практики решения проблем и задач для создания специалистов по решению проблем в реальном мире. 3
Этот подход включает решение проблем на протяжении каждого урока и поощряет частую практику как в вычислениях, так и в решении проблем.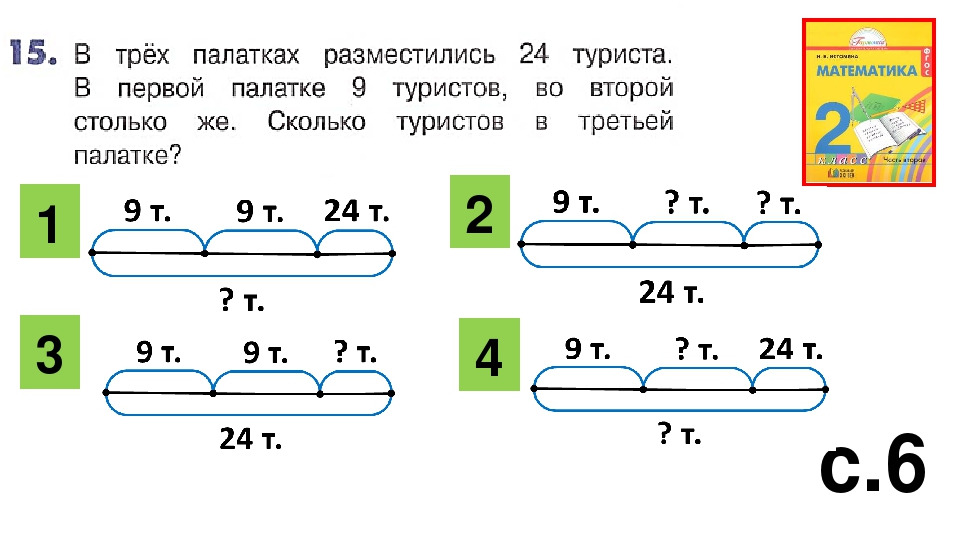 Словесные задачи появляются в каждой главе и переходят от 1 шага к 2 шагам и многоступенчатым. Каждая глава завершается сложной задачей или набором задач, требующих от студентов решения некоторых нестандартных вопросов. Чтобы решить эти проблемы, учащимся необходимо использовать свои глубокие предыдущие знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочение, идентификацию частей и целого, выявление закономерностей и отношений, индукция и дедукция и пространственная визуализация.
Словесные задачи появляются в каждой главе и переходят от 1 шага к 2 шагам и многоступенчатым. Каждая глава завершается сложной задачей или набором задач, требующих от студентов решения некоторых нестандартных вопросов. Чтобы решить эти проблемы, учащимся необходимо использовать свои глубокие предыдущие знания, а также недавно приобретенные концепции и навыки, сочетая стратегии решения проблем с навыками критического мышления, включая классификацию, сравнение, упорядочение, идентификацию частей и целого, выявление закономерностей и отношений, индукция и дедукция и пространственная визуализация.
Текст для второго класса начинается с цифр до 1000. Учащиеся начинают с выражения чисел в стандартной форме (231), развернутой форме (200 + 30 + 1) и словарной форме (двести тридцать один). Это сопровождается конкретными представлениями с помощью базовых десяти блоков, а для двухзначных чисел и нескольких трехзначных чисел — представление цепочкой стержней длиной 1, 10 и 100. Эта начальная глава также включает в себя последовательность чисел и сравнение с использованием большего, чем и меньше терминологии, а затем сразу переходя к сложению и вычитанию двух- и трехзначных чисел.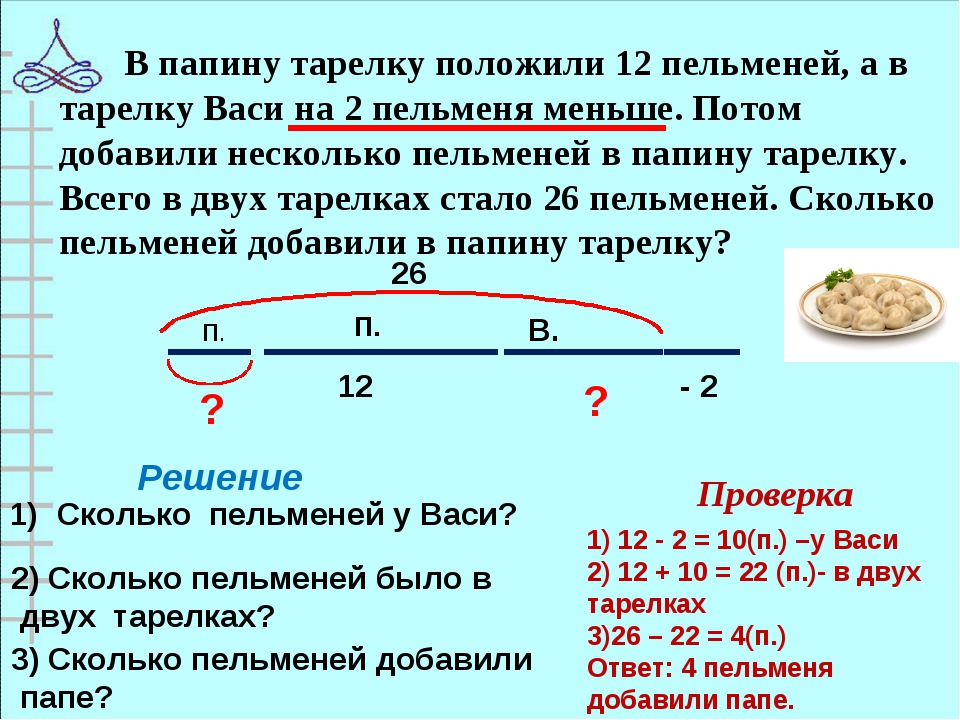 Здесь должен быть вывод, если у вас еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.
Здесь должен быть вывод, если у вас еще сотни, десятки и единицы не имеют никакого / большого значения; и если у вас столько же сотен, но больше десятков, то единицы не имеют большого значения. Большинство моих учеников (если не все) борются с самого начала! Похоже, у них нет прочного основания для понимания чисел до 100 или концепции разряда в целом. Этот модуль разработан для того, чтобы опередить разочарование, которое студенты испытывают, когда их слишком быстро подталкивают, прежде чем они получат твердое представление о принципах позиционной ценности и свойствах операций.
Этот модуль открывает учебный год с одноступенчатых задач на сложение и вычитание всех типов с использованием чисел до 10. Цель состоит в том, чтобы потратить время на отработку основных вычислений с числами, с которыми ученик сможет комфортно работать, прежде чем сразу перейти к школьной программе. Как только будет достигнут уровень понимания этих наборов задач (числа до 10), учащиеся перейдут к решению одноэтапных задач, используя числа для подростков, а затем к числам до 100. Большинство задач учебной программы в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро перейдут к задачам с числами до 100 и будут готовы работать по обычной учебной программе.
Большинство задач учебной программы в начале года требуют добавления и вычитание 3-значных чисел.Некоторые учащиеся быстро перейдут к задачам с числами до 100 и будут готовы работать по обычной учебной программе.
На протяжении всего курса основное внимание будет уделяться решению, а затем и составлению набора словесных задач, обеспечивающих надежную и сбалансированную практику. Наборы задач будут основаны на сценарии, который раскрывает суть истории. Каждый сценарий позволит нам решить несколько проблем, изменив числа и убедившись, что каждый набор чисел представляет собой разумную проблему.Эта идея выглядит следующим образом: У Джона в коробке 8 мелков. Он делит 3 с Сэмом. Сколько мелков осталось у Джона в коробке? В коробке у Джона есть мелки. Он делит 3 с Сэмом. У Джона осталось 5 мелков в коробке. Со скольких мелков Джон начал? У Джона 5 цветных карандашей. У Сэма на 2 меньше, чем у Джона. Сколько мелков у Сэма? Джон и Сэм делятся мелками. У Джона их 5, а у Сэма 3. Сколько карандашей у друзей вместе? Два ученика участвуют в нескольких рассказах, связанных с обменом карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и прямолинейны, а другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. 4
Сколько карандашей у друзей вместе? Два ученика участвуют в нескольких рассказах, связанных с обменом карандашами, в которых используется один и тот же набор чисел, но в немного разных ситуациях.Некоторые ситуации более очевидны и прямолинейны, а другие требуют больше размышлений. Важно предоставить учащимся возможность работать и решать различные типы задач, которые можно создать из одного набора чисел. 4
Таксономия типов задач на сложение и вычитание, определенная в Глоссарии общих основных государственных стандартов математики, представляет собой структуру, которая разделяет одноэтапные задачи на три широких класса: изменить , сравнение и частично-частично-целое .Затем каждый из трех классов разделяется на 14 типов задач, отсортированных следующим образом: изменение , в котором некоторое количество либо добавляется к другому количеству, либо отнимается от него с течением времени; сравнение , в котором одна сумма описывается как больше или меньше другой суммы; и частично-частично-целое , в котором сумма состоит из двух частей. 5
5
В группе проблем изменения есть две подгруппы: изменение-увеличение , в которой количество добавляется к начальной сумме, и изменение-уменьшение , в которой количество берется из начальной суммы.Мы можем узнать эти подгруппы более привычно как «добавить к» или «взять от». Кроме того, в каждой из этих подгрупп существует три возможных неизвестных величины. Один сценарий, показывающий изменение-увеличение : 2 котенка играли с пряжей. К ним присоединяются еще 3 котенка. Сейчас 5 котят играют с пряжей. Используя эти количества, неизвестное может быть результатом (2 + 3 =?), Неизвестной величиной изменения (2 +? = 5) или неизвестной начальной суммой (? + 3 = 5). В подгруппе «изменение-уменьшение» снова есть три возможных неизвестных.Сценарий для этого примера: на ветке сидят 5 птиц. 2 улетают. Теперь на ветке сидят 3 птицы. Здесь ученики снова могут решить окончательную сумму (5 — 2 =?), Сумму сдачи (5 -? = 3) или начальную сумму (? — 2 = 3). Это дает все шесть типов проблем с изменениями.
Это дает все шесть типов проблем с изменениями.
Аналогично сравнение проблемы также можно разделить на две подгруппы: сравнение-больше , в котором одна величина описывается как больше или больше, чем другая, и -меньше сравнения, , в которой одна величина описывается как меньше или меньше. чем другой.Здесь снова каждая из этих двух подгрупп имеет три возможных неизвестных, всего 6 типов. У Сэма 6 шариков. У Джеймса 8 шариков. У Джеймса на 2 шарика больше, чем у Сэма. Неизвестным количеством может быть меньшее количество (? + 2 = 8), неизвестное большее количество
(6 + 2 =?), Или неизвестная разница (8-6 =?), Одна величина больше и одна меньше. Используя этот же сценарий для набора задач без сравнения, язык необходимо изменить с «больше чем» на «меньше чем».Вот как можно представить этот набор с настройкой языка: у Сэма 6 шариков. У Джеймса 8 шариков. У Сэма на 2 шарика меньше, чем у Джеймса.
Часть-часть-целое Задачи — это набор двух величин, частей, которые вместе составляют целое количество.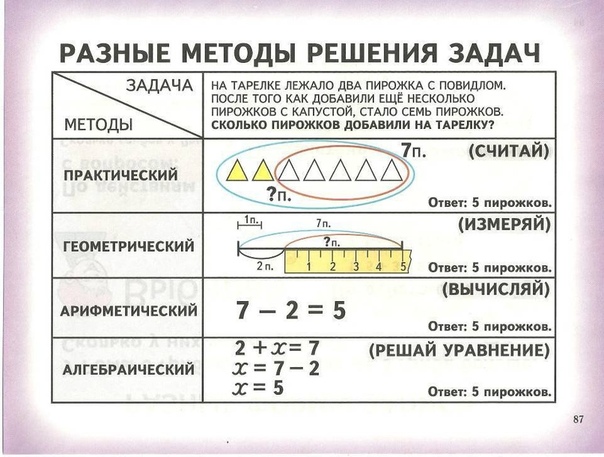 Этот тип проблемы кажется очень похожим на , изменяющий категорию , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо все неизвестно.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе проблем всего 2 типа.
Этот тип проблемы кажется очень похожим на , изменяющий категорию , но в этом типе проблемы нет никаких изменений с течением времени. Две части играют эквивалентные роли, что позволяет использовать только две возможные неизвестные категории: либо часть неизвестна, либо все неизвестно.Есть 4 большие собаки и 3 маленькие собаки. Всего 7 собак. Одна из частей может быть неизвестной (4 +? = 7 или? + 3 = 7) или неизвестным может быть размер целого (4 + 3 =?). Поскольку детали взаимозаменяемы, в этом классе проблем всего 2 типа.
На следующей диаграмме эти классы и категории сортируются по структуре. В Приложении A к этому модулю приведен набор примеров проблем, иллюстрирующих каждый из этих 14 типов.
Тип проблемы | Сумма неизвестна | ||||
Изменение | Увеличение Дополнение к | Начальный | Изменение | Финал | |
Уменьшение Вычесть из | Начальный | Изменение | Финал | ||
Сравнение | Большой / Подробнее | Меньший | Большой | Разница | |
Меньше / Меньше | Меньший | Большой | Разница | ||
Частично-частично-целое | Часть | Всего | |||
Сценарии проблем
Для второклассников школьная жизнь — это большая часть их мира. Большинство моих учеников приехали в Эджвуд на год детского сада и остались до первого класса, так что год во втором классе, по сути, стал третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут в базовом понимании контекста.
Большинство моих учеников приехали в Эджвуд на год детского сада и остались до первого класса, так что год во втором классе, по сути, стал третьим годом в той же школе. Им комфортно в здании, и они знают многих других студентов. Они станут активными участниками математических историй, которые мы будем строить вместе. Действия, которые происходят в классе, в кафетерии, на детской площадке и в автобусе, кажутся узнаваемыми ситуациями, которые помогут в базовом понимании контекста.
Кроме того, у учащихся есть возможность включить темы и изучить другие предметы, такие как наука, общественные науки, грамотность, искусство, музыка и, в нашей школе, танцы и драма. Одним из примеров может быть создание набора задач-рассказов, посвященных жизненному циклу бабочки, единице изучения каждый год во втором классе. Обладая общими знаниями, которые получат студенты, этот контент может стать сценарием текстовых задач. Примером может быть: Семь гусениц поднялись по ветке и образовали куколки. Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе как класс, может дать персонажей новый набор задач. У Любопытного Джорджа была связка бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При установленном сценарии ученики будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.
Позже в тот же день еще три гусеницы поднялись по ветке и образовали куколки. Сколько кукол свешивается с ветки? Точно так же использование персонажей в книге, прочитанной вместе как класс, может дать персонажей новый набор задач. У Любопытного Джорджа была связка бананов. Он съел 4 из них. Теперь у него 3. Сколько бананов начал любопытный Джордж? Использование общего или тематического контента не только объединит все мышление и практику, но и предоставит осязаемые и реальные ситуации.При установленном сценарии ученики будут работать с набором чисел, определяя неизвестное в рамках каждого типа задач.
Создание проблем
Вопрос, на который часто задают предположение: «Что мы должны сделать, чтобы ответить на вопрос, чтобы решить проблему со словом?» Фундаментальное понимание того, что задают, не очевидно для студентов, что делает решение недоступным. Большинство первоклассников, поступающих во второй класс, имеют базовое понимание, когда история (проблема) классифицируется как окончательное неизвестное или целиком неизвестное , но большинство других компонентов таксономии им незнакомы или слишком сложны для декодирования. Чтобы помочь им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие базовые материалы в классе — карандаши, блокноты, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.
Чтобы помочь им в их мышлении, они будут использовать конкретные модели, такие как они сами (2 ребенка сидят за столом для чтения, еще 4 присоединяются к ним), разыгрывая сценарии. Многие базовые материалы в классе — карандаши, блокноты, папки, мелки — можно использовать для создания и разработки сценариев с учетом каждого типа проблемы.
Решение проблем
Следуя общему плану программы Singapore Math, студенты будут решать задачи, используя конкретный, графический и абстрактный подход.Поскольку это стандартный подход к обучению математике в нашем округе в течение года, учащиеся начнут с этого набора стратегий для решения наборов задач.
Задачи со словами написаны в виде рассказов и сценариев, поэтому язык необходимо учитывать при составлении задач для начинающих второклассников. Задачи со словами связаны с языком и чтением не меньше, чем с математикой. Если история непонятна, как студенты могут начать понимать, что им делать с числами, которые им дали, и заданным вопросом? Таким образом, слова и словарный запас должны быть подходящими и полезными для различных уровней чтения поступающих студентов. Структура словесных задач должна быть понятной и ясной, доступной как языком, так и цифрами. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы он был знаком всем учащимся.
Структура словесных задач должна быть понятной и ясной, доступной как языком, так и цифрами. Кроме того, следует обсудить язык, особенно слова, которые выражают взаимосвязь между задействованными величинами, чтобы он был знаком всем учащимся.
Это явная интеграция языковых искусств и математики и метода, с помощью которого учащиеся могут связать математику с реальным миром, в данном случае, посредством занятий, которыми они занимаются в школе. Навыки чтения и вычисления сочетаются даже с простейшими задачами со словами.
Структура коллекции задач
Введение в содержание этого раздела включает в себя определенную последовательность и основы, которые помогут студентам решить 14 типов задач. Чтобы начать раздел, учащиеся будут работать только с числами до 10. Это важная отправная точка для обеспечения понимания. Большинство моих второклассников умеют складывать и вычитать до 10, но не очень хорошо владеют языком проблемных слов. Итак, во-первых, ученикам будет больше интересна язык, чем арифметика. Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегии и уверенность!
Студенты будут практиковаться в выяснении того, что именно задают проблемы, с проблемами, с которыми они знакомы, прежде чем перейти к новому этапу. Выполнение всех типов задач улучшит и увеличит стратегии и уверенность!
Когда освоено сложение и вычитание в пределах 10, следующая фаза единицы переходит к числам до 20. Ключевым моментом является продолжение сценариев, которые очевидны и повторяются по мере введения новых чисел. Примером этого перехода могут быть следующие параллельные задачи:
На первой остановке в автобус сели 6 студентов.На второй остановке в автобус сели 3 студента. Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 3 студента. Сейчас в автобусе 9 студентов. Сколько студентов сели на первую остановку? ( изменение-увеличение, изначально неизвестно)
Теперь они становятся:
На первой остановке в автобус сели 11 студентов. На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
На второй остановке в автобус сели 7 студентов.Сколько студентов в автобусе после второй остановки? ( изменение-увеличение, окончательное неизвестно)
Некоторые студенты сели в автобус на первой остановке. На второй остановке в автобус сели 7 студентов. Сейчас в автобусе 18 студентов. Сколько студентов сели на первую остановку? ( изменение-увеличение, изначально неизвестно)
При работе с числами до 20 важно, чтобы учащиеся понимали, что «подростковые» числа (11-19) на самом деле равны 10 и некоторым единицам. Студенты должны работать с числами в пределах 20, составляя уравнения, используя свои знания и умение составлять первую десятку.В случае 7 + 6 создание новой десятки выглядит так:
7 + 6 = 7 + 3 + 3 = 10 + 3 = 13
Поскольку 7 требует 3, чтобы получить десять, а 6 состоит из 3 + 3, это уравнение показывает последовательность создания 10 и некоторых других. Практика этого метода с использованием двух десятков фреймов наглядно демонстрирует процесс.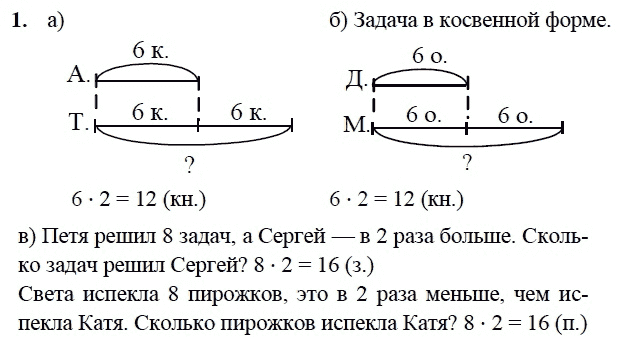 В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.
В приведенном выше примере учащиеся используют десять кадров, чтобы показать 7 и 6 отдельно. Чтобы получить новые 10, ученики переместят 3 из 6, которые теперь показывают 10 и еще 3 или 13.
Как упоминалось ранее, очевидно, что наиболее доступными типами задач для учеников, поступающих во второй класс, являются изменение-увеличение или изменение-уменьшение, результат неизвестен и частично-частично-целое, целое неизвестно. Общая стратегия решения задачи со словами, кажется, состоит в том, чтобы просто взять два числа, которые вы видите, и сложить их или, возможно, вычесть их, но часто студенты просто не уверены. Похоже, что это наиболее часто используемые типы задач, что оставляет учащихся без сбалансированного опыта работы со всеми 14 типами и, в конечном итоге, без некоторых стратегий, которые можно использовать при решении задач.Студенты должны увидеть широкий круг задач, чтобы получить четкое представление о том, как используются сложение и вычитание и как они связаны друг с другом. Понятие достаточности примеров означает, что учащимся следует ознакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Понятие достаточности примеров означает, что учащимся следует ознакомиться с широким спектром примеров, чтобы обеспечить всестороннюю практику с концепцией. 6
Подходы к данной учебной программе различаются в зависимости от стиля обучения всех учащихся.
Общий формат основан на модели мастерской. Концепции и навыки преподаются с помощью серии мини-уроков, ориентированных на достижение цели, с использованием следующих методов:
Практическое обучение: Большинству молодых студентов необходимо начинать с практического обучения.Использование конкретных моделей для разработки математических рассказов позволяет учащимся увидеть проблему и манипулировать элементами по мере развития рассказа. Этот тип обучения — важный первый шаг.
Дифференцированное обучение: уроки и упражнения будут нацелены на максимальное обучение. Студенты будут использовать различные подходы, работая иногда индивидуально, а иногда в небольших группах, в зависимости от сложности работы. Некоторые студенты будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Некоторые студенты будут двигаться быстрее по мере овладения навыками, а некоторым потребуется больше возможностей для практики.
Совместное обучение: ученикам будет предоставлена возможность работать в совместных группах над созданием математических рассказов для представления классу. Эта стратегия позволит студентам работать совместно, выполняя различные роли, необходимые для завершения работы, с акцентом на успех для всех.
Задание 1: Упорядоченные типы проблем — Проблемы до 10
Вводная (и обзорная) часть модуля охватывает все типы проблем, но в определенной последовательности. Цель состоит в том, чтобы студенты прочитали и интерпретировали словесную задачу с помощью инструкций, а затем самостоятельно попрактиковались.Из-за множества типов задач эта часть займет несколько дней повторения и практики, прежде чем учащиеся научатся писать собственные наборы задач. В зависимости от потребностей учащихся и темпа понимания, я ожидаю, что этот раздел будет продолжаться от четырех до шести дней, а при необходимости и больше.
Последовательность следующая: часть-часть-целое ; изменение-увеличение и изменение-уменьшение ; и, наконец, сравните больше и сравните меньше .Следующие вводные занятия разработаны как групповое мероприятие, когда ученики либо сидят за партами, либо собираются на ковре рядом с доской или мольбертом. Вся групповая часть должна составлять максимум 20 минут. В конце каждого занятия я предлагаю студентам решить от 5 до 10 похожих задач. Более способные студенты могут начать создавать свои собственные проблемы во время самостоятельной работы.
Начало с основ дает хорошую возможность познакомиться с навыками студентов, что помогает при подготовке дифференцированной работы и создании групп,
На этом уроке учащиеся будут интерпретировать проблемы реального мира и с помощью манипуляторов и картинок решать истории частично-частично-целиком, используя сложение и вычитание.
Играют 6 девочек
С ними играют 3 мальчика.
Сколько всего детей играет?
Начните рассказ с всего неизвестного, как в этом примере. Этот тип историй идеально подходит для того, чтобы ученики разыгрывали прямо в классе. Напишите рассказ на доске или листе с диаграммами и попросите учащихся выступить в качестве актеров. Когда ученики решат задачу, напишите математическое предложение, чтобы показать, что произошло: 6 + 3 = 9 учеников. Объясните, что две части (мальчики и девочки) составили единое целое (детей).Пока студенты все еще находятся в актерской позиции, представьте новый подход к этому сценарию:
Играют 9 учеников.
Из них 6 девочек.
Сколько мальчиков играет?
На этом наглядном примере ученики должны сразу увидеть, сколько. Важная концепция, которую следует продемонстрировать, заключается в том, что части могут быть определены, когда известны целое и одна часть, в этом случае 9 известно как целое, а 6 как одна часть. Опять же, напишите математическое предложение, чтобы показать этот расчет: 6 +? = 9 и включите стратегию начала с целого, чтобы определить недостающую часть как предложение вычитания 9-6 = 3. Практика обоих подходов к решению поможет учащимся соединить сложение и вычитание и понять, как они используются вместе.
Практика обоих подходов к решению поможет учащимся соединить сложение и вычитание и понять, как они используются вместе.
Поскольку на этом уроке учащиеся должны читать задачи-рассказы, я объединю беглых читателей с теми, кто не владеет свободно, предоставлю счетчики тем, кто их хочет, и позволю партнерам работать вместе для решения проблем и поделиться стратегиями, которые они использовали.
Я воспользуюсь еще двумя примерами, подобными приведенным ниже, для демонстрации, не забывая писать на доске слово «задача», а также математическое предложение.Я также перефразирую проблемы, чтобы часть была неизвестной.
У Ханны 5 красных маркеров.
У нее 3 синих маркера
Сколько всего маркеров у Ханны?
7 учеников рисуют мелками.
2 ученика рисуют цветными карандашами.
Сколько учеников рисуют?
Продолжая эту же идею, следующий набор типов задач включает изменение-увеличение и изменение-уменьшение . Хотя часть-часть-целое — это язык, который учащиеся могут усвоить и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменение больше подходит для студентов, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из начальной суммы.
Хотя часть-часть-целое — это язык, который учащиеся могут усвоить и использовать при обсуждении своей работы, язык изменение-увеличение и изменение уменьшение немного сложнее. Использование слова изменение больше подходит для студентов, чтобы продемонстрировать, что некоторая сумма была либо добавлена, либо вычтена из начальной суммы.
Введите слово «проблема» ниже, которое является примером неизвестного результата в категории «изменение-увеличение».
У Джейсона в начале дня было 8 наклеек с надписью «поймал себя на хорошем счету».
За школьный день он заработал еще 2 стикера.
Сколько наклеек у Джейсона на графике в конце дня?
Студент может решить задачу, как написано, и, используя тот же сценарий, предложить им создать историю без изменений и начальную неизвестную историю . Один из примеров:
У Джейсона на графике
было несколько наклеек «пойманный на хорошем». начало дня.
За школьный день он заработал еще 2 стикера.
В итоге у него 10 наклеек.
Сколько наклеек было у Джейсона в начале дня?
Это устное задание, в котором я напишу скорректированную версию по всем направлениям, поместив математическое предложение внизу. Важно позволить учащимся поработать над составлением задачи, чтобы они могли начать видеть взаимосвязь между проблемами и тем, что они задают.
Результат Неизвестно Версия 8 + 2 =? | Изменение Неизвестно Версия 8+? = 10 | Начальный Неизвестно Версия ? + 2 = 10 |
Цель состоит в том, чтобы учащиеся поняли, а не просто решили.Я могу неформально оценить во время обсуждения переписывания текста слово «проблема», с более формальной оценкой позже в разделе.
Следующая категория, которую мы представим, — это типов задач «изменение-уменьшение» . Следуя тому же формату, что и раньше, я представлю результат неизвестно, заменим неизвестное , а затем начальное неизвестное.
Следуя тому же формату, что и раньше, я представлю результат неизвестно, заменим неизвестное , а затем начальное неизвестное.
Кристалл собрала 7 листов для своего проекта.
2 листа унесло ветром.
Сколько листьев у Кристалл осталось для своего проекта?
Результат Неизвестно 7 — 2 =? | Изменение Неизвестно 7 -? = 5 | Начальный Неизвестно ? — 2 = 5 |
Опять же, цель состоит в том, чтобы учащиеся понимали, а не просто решали.
Третий широкий класс, сравните, сложнее для моих 2 и учеников. Это требует, чтобы текст словесных задач был очень простым. Студенты не должны путаться, когда они учатся извлекать данные из задачи. Помните, что использование точной терминологии — это не цель, а, скорее, понимание сути проблемы. Вот три способа, которыми я представлю сценарий, который показывает типы проблем сравнение-больше , и три способа показать без сравнения. Студенты должны быть знакомы и иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе с диаграммами и вывешиваю их в классе, ученики могут начать видеть и сравнивать и противопоставлять их, поскольку один сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере введения и работы над набором задач. Моя роль здесь — позволить ученикам начать замечать тонкие различия в формулировках и том, как они меняют мышление.Лучше начать с простого!
Студенты должны быть знакомы и иметь возможность практиковать все типы. Конечно, не все эти примеры следует использовать одновременно. Когда я записываю задачи на листе с диаграммами и вывешиваю их в классе, ученики могут начать видеть и сравнивать и противопоставлять их, поскольку один сценарий объясняется по-разному. Использование слов «больше» и «меньше» должно быть выделено и объяснено по мере введения и работы над набором задач. Моя роль здесь — позволить ученикам начать замечать тонкие различия в формулировках и том, как они меняют мышление.Лучше начать с простого!
У Оливии на 4 ластика больше, чем у Джона. У Джона 2 ластика. Сколько ластиков у Оливии? (сравнение-больше, большее неизвестно) 2 + 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Джона 2 ластика. Сколько ластиков у Оливии? (без сравнения, большее неизвестно) 4 + 2 =? |
У Оливии на 4 ластика больше, чем у Джона. У Оливии 6 ластиков. Сколько ластиков у Джона? (сравнение больше, меньше неизвестно) 6 — 4 =? | У Джона на 4 ластика меньше, чем у Оливии. У Оливии 6 ластиков. Сколько ластиков у Джона? (без сравнения, меньше неизвестно) 6 — 4 =? |
У Оливии 6 ластиков. У Джона 2 ластика. На сколько ластиков у Оливии больше, чем у Иоанна (сравнение-подробнее, разница неизвестна 6 — 2 =? 2+? = 6 | У Джона 2 ластика. У Оливии 6 ластиков. На сколько ластиков у Джона меньше, чем у Оливии? (без сравнения, разница неизвестна) 6 — 2 =? |
На протяжении этих вводных занятий мы со студентами будем обсуждать сценарии, которые в конечном итоге можно будет использовать в собственных текстовых задачах.Идеи должны генерироваться на основе школьных занятий и материалов, побуждая учащихся задуматься о том, что ученики могут фактически использовать для манипуляций или, как в первом сценарии, уметь действовать, чтобы решить. Сохраняя список идей на бумаге с диаграммами в качестве справочного материала, учащиеся не будут бороться со словарным запасом или подходящими сценариями; им предстоит решить свои проблемы. Этот список подготовит студентов ко второй части раздела.
Сохраняя список идей на бумаге с диаграммами в качестве справочного материала, учащиеся не будут бороться со словарным запасом или подходящими сценариями; им предстоит решить свои проблемы. Этот список подготовит студентов ко второй части раздела.
Мероприятие 2: Классные / школьные сценарии
Как было сказано ранее, слова и словарный запас должны быть доступны для учащихся, а не должны быть проблемой или препятствием.Цель состоит в том, чтобы продумать истории и использовать информацию, собранную во время мозгового штурма. Чтобы начать эту часть, просмотрите диаграммы и добавьте больше, если у учащихся появятся новые идеи. При составлении задач со словами может быть полезно иметь информацию в категориях, например:
Используемые нами материалы
Классы, которые мы посещаем
Занятия в школе
Имена одноклассников
Я создам группы из двух или трех учеников, чтобы они написали свои собственные задачи и поделились с классом.Поскольку этот урок требует, чтобы учащиеся читали и писали задачи-рассказы, опять же, беглые читатели и писатели с теми, кто не владеет свободно, предоставляют счетчики тем, кто их хочет, и позволяют партнерам работать вместе над решением проблем и делиться стратегиями, которые они использовали. .
.
Цель в этот период времени — предложить учащимся написать ту же задачу, но попробовать по-другому, выбрать другой тип, когда они рассказывают историю. Время для совместной работы групп студентов будет во время прибытия в качестве утренней работы и во время части математического семинара во время обучения математике.Это позволит учащимся работать со своими партнерами по 30 минут в день над созданием математических рассказов.
Подчеркну, что важно хранить их коллекцию вместе, поскольку большая часть их работы станет частью рабочей тетради, которую они создадут в конце этого раздела. Папки и математические журналы могут быть полезны, или мой ежедневный сбор незавершенной работы — еще один вариант.
Мероприятие 3: Научные сценарии
Первым разделом науки 2 и является исследование жизненного цикла бабочки.Студенты получают гусениц в начале семестра и наблюдают и записывают изменения в жизни гусениц. Работа, которую студенты выполняют на уроках естествознания, может стать информацией и сценариями, которые они могут использовать для составления текстовых задач.
Используя все типы задач, мы напишем несколько вместе как класс. Это дополнительная возможность очень конкретно интегрировать математику в наши научные исследования и работу. Студентам важно осознавать, что, хотя их обучение было разделено на предметные области, по сути, невозможно разделить все это на категории.Таким образом, в этой части модуля используются математика, естественные науки и чтение, чтобы помочь учащимся узнать о жизненном цикле бабочки (а также других животных).
Учащиеся будут создавать наборы задач, используя свой ежедневный опыт отслеживания своих гусениц. У каждого ученика есть 2-3 гусеницы, за которыми нужно наблюдать и записывать информацию, что может стать началом словесных задач. Примеры для начала: если в таблице 3 8 гусениц и 2 гусеницы присоединяются к этой группе, сколько гусениц наблюдается в таблице 3? В классе 28 учеников.Каждому ученику требуется одна чашка еды для гусениц. Есть 30 чашек корма для гусениц. На сколько чашек еды больше, чем у студентов?
Часто встречаются студенты, которые проявляют большой интерес к другим областям науки. Это область, которую следует поощрять, если учащиеся хотят поделиться своими знаниями. Некоторые студенты будут более склонны использовать единицу обучения, проводимую в классе, но на протяжении дня, посвященного грамотности, учащиеся знакомятся с большим количеством научно-популярной литературы или информационного текста, который, безусловно, может обогатить наши научные задачи. .
Это область, которую следует поощрять, если учащиеся хотят поделиться своими знаниями. Некоторые студенты будут более склонны использовать единицу обучения, проводимую в классе, но на протяжении дня, посвященного грамотности, учащиеся знакомятся с большим количеством научно-популярной литературы или информационного текста, который, безусловно, может обогатить наши научные задачи. .
На протяжении всего раздела по естествознанию студенты будут продолжать писать текстовые задачи различных типов, чтобы в конечном итоге включить их в наш последний проект — рабочую тетрадь. Эти задачи можно писать во время утренней рабочей сессии, во время семинара по математике и в конце урока естествознания. К концу раздела у каждого студента должно быть две задачи, которые нужно добавить в раздел «Наука» в учебном пособии.
Мероприятие 4: Создание Рабочей тетради / Празднование публикации
Целью этой части модуля является сортировка словесных задач по «главам» и создание рабочей тетради для публикации на праздновании публикации. Главы будут названы по предметам или категориям, в зависимости от выбора ученика и предложения учителя. Идеи включают в себя рассказы для начинающих, занятия в классе, развлечения на детской площадке, науку и математику и связи с общественными исследованиями. Пусть студенты творчески подходят к названиям!
Главы будут названы по предметам или категориям, в зависимости от выбора ученика и предложения учителя. Идеи включают в себя рассказы для начинающих, занятия в классе, развлечения на детской площадке, науку и математику и связи с общественными исследованиями. Пусть студенты творчески подходят к названиям!
Студенты представят свои работы, которые будут включать как минимум одно словесное задание для каждой главы. Они также должны представить решения своих проблем, чтобы их можно было включить в ключ ответа. В каждой главе будет не менее 25 задач с примерами всех типов и с разным уровнем сложности.Задачи со словами могут быть напечатаны или написаны от руки для окончательной рабочей тетради, в зависимости от того, что учащиеся решат в классе. Для празднования необходимо будет скопировать и каким-либо образом переплести одну рабочую тетрадь на каждого учащегося.
За две недели до Праздника публикации студенты создадут приглашение, чтобы передать его семье и друзьям, приглашая их прийти на «Праздник решения проблем». Родители и другие VIP-гости потратят некоторое время на работу над задачами со словами, перемещаясь по комнате, навещая многих студентов.Студенты поделятся с гостями своей собственной работой (словесные задачи, которые они сами создали) и «помогут» посетителям найти ответы.
Родители и другие VIP-гости потратят некоторое время на работу над задачами со словами, перемещаясь по комнате, навещая многих студентов.Студенты поделятся с гостями своей собственной работой (словесные задачи, которые они сами создали) и «помогут» посетителям найти ответы.
У каждого студента будет лист «Комментарии», который гости смогут подписать и оставить комментарии о своем опыте работы со студентом. Я рекомендую посетителям остановиться, чтобы поговорить с каждым студентом или с любым другим студентом во время их посещения.
Кроме того, это возможность предложить студентам работать редакторами и издателями.Создание рабочей книги потребует времени на просмотр и сборку, и эти задачи могут быть делегированы заинтересованным учащимся и разделены ими.
Общие государственные стандарты по математике,
http://www.corestandards.org/the-standards/mat Mathematics.
Фонг, Хо Кхеонг. Математика в фокусе Сингапурская математика Маршалла Кавендиша . Итоговая ред. Сингапур: Marshall Cavendish Education, 2015.
Итоговая ред. Сингапур: Marshall Cavendish Education, 2015.
Фусон, Карен К. Математические выражения . Издание 2011 г. Орландо, Флорида: Houghton Mifflin Harcourt;, 2011.
Хау, Роджер. Три столпа математики для первого класса и не только
Howe, Roger, Самое важное для вашего ребенка в арифметике
Хау, Роджер и Гарольд Рейтер, Пять ступеней определения стоимости
Ma, L. Знание и преподавание элементарной математики , Erlbaum Associates, Махва, Нью-Джерси, 1999.
Пазлы «Москва»: 359 математических увлечений . Нью-Йорк: Dover Publications, 1992.
Поля, Георгий. Как решить: новый аспект математического метода . Издание Новой Принстонской научной библиотеки, 2014.
Изменение Увеличение / Результат Неизвестен
На занятиях 7 учеников. К ним присоединяются еще 2 студента. Сколько учеников сейчас в классе?
К ним присоединяются еще 2 студента. Сколько учеников сейчас в классе?
Изменение Увеличение / Изменение Неизвестно
На занятиях 7 учеников.К ним присоединяются еще несколько студентов. Тогда было 9 студентов. Сколько студентов попадают в первые 7?
Увеличение изменений / начальное значение неизвестно
Некоторые ученики на занятиях. К ним присоединились еще 2 студента. Тогда было 9 студентов. Сколько учеников было в классе вначале?
Изменение Уменьшение / Результат Неизвестен
На занятиях находилось 9 учеников. 2 студента ушли домой. Сколько учеников сейчас в классе?
Изменение Уменьшение / Изменение Неизвестно
На занятиях находилось 9 учеников.Некоторые студенты разошлись по домам. Сейчас здесь 7 студентов. Сколько студентов ушли домой?
Изменение Уменьшение / Исходное значение Неизвестно
Некоторые ученики были в классе. 2 студента ушли домой. Тогда в классе было 7 учеников. Сколько учеников было в классе вначале?
Сравнить больше / Разница неизвестна
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько больше у Сэма, чем у Эмили?
У Эмили 6 картошек фри. Насколько больше у Сэма, чем у Эмили?
Сравнить Больше / Больше неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили.У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Сравнить Больше / Меньше Неизвестно
У Сэма на 4 картофеля фри больше, чем у Эмили. У Сэма 10 картошек фри. Сколько картофеля фри у Эмили?
Сравнить Меньше / Разница неизвестна
У Сэма 10 картошек фри. У Эмили 6 картошек фри. Насколько у Эмили меньше, чем у Сэма?
Сравнить Меньше / Меньше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Сэма 10 картошек фри.Сколько картофеля фри у Эмили?
Сравнить Меньше / больше Неизвестно
У Эмили на 4 картофеля фри меньше, чем у Сэма. У Эмили 6 картошек фри. Сколько картофеля фри у Сэма?
Частично-Частично-Целое / Целое Неизвестно
У Сэма 4 печенья на обед. У него еще 2 на ужин. Сколько файлов cookie у Сэма?
Частично-Частично-Целое / Целое Неизвестно
Сэм сегодня съел 6 печенек. У него было 4 штуки на обед. Сколько он ел на обед?
У него было 4 штуки на обед. Сколько он ел на обед?
Этот модуль, естественно, объединяет грамотность и математику.Как чтение, так и письмо являются неотъемлемой частью способности учащихся решать словесные задачи, включая сложение и вычитание.
Учащиеся будут работать в соответствии с Общим основным государственным стандартом по математике, 2.OA.A.1, который гласит, что второклассники должны к концу года уметь «представлять и решать задачи, включающие сложение и вычитание в пределах 100». для решения одноэтапных задач со словами, включающих ситуации сложения, взятия из, объединения, разборки и сравнения с неизвестными во всех позициях.Во время этого раздела учащиеся начнут решать и составлять словесные задачи с числами до 10, переходить к числам до 20 и переходить к 100 и до 1000 по мере того, как они усваивают концепцию значения места.
В этом разделе также рассматриваются Общие основные государственные стандарты чтения информационного текста, RI.2.1, в которых учащиеся работают над поиском ключевых идей и деталей, задавая и отвечая на такие вопросы, как кто, что, где, когда, почему и как продемонстрировать понимание ключевых деталей текста. На протяжении этого раздела, посвященного задачам со словами, учащиеся будут работать, задавая эти вопросы, чтобы определить, какую информацию дает математический рассказ. Когда они начнут писать свои собственные текстовые задачи, им нужно будет рассмотреть эти вопросы, чтобы составить содержательный рассказ для текста своей проблемы.
На протяжении этого раздела, посвященного задачам со словами, учащиеся будут работать, задавая эти вопросы, чтобы определить, какую информацию дает математический рассказ. Когда они начнут писать свои собственные текстовые задачи, им нужно будет рассмотреть эти вопросы, чтобы составить содержательный рассказ для текста своей проблемы.
- Общие основные государственные стандарты по математике, http://www.corestandards.org/the-standards/mat Mathematics.
- Общие основные государственные стандарты по математике
- Хо Кхеонг Фонг, Математика в фокусе Сингапура Математика Маршалла Кавендиша , 8.
- Роджер Хоу, Три столпа математики для первого класса и не только, 2 .
- Роджер Хоу, Три столпа математики для первого класса и не только, 1 . Общие основные государственные стандарты по математике
- Роджер Хоу, Три столпа математики для первого класса и не только, 2
Mathwire.
 com | Решение проблем: Gr. К-2 Главная |
Список от А до Я |
Стандарты |
Темы
com | Решение проблем: Gr. К-2 Главная |
Список от А до Я |
Стандарты |
Темы Ресурсы по решению проблем: K-2
Решение задач: классы К-2
Эти задачи предназначены для учащихся классов K-2:
- Пазлы на сотнях квадратов: Учащиеся школы Порт-Монмут-Роуд в Кинсбурге, штат Нью-Джерси, используют шаблоны для сборки сотен головоломок.& nbsp Учителя создают головоломки, которые различаются как по количеству, так и по размеру частей, чтобы дифференцировать это задание и наилучшим образом удовлетворить разнообразные потребности учащихся в классе.
- Задачи о животных просят учащихся решать задачи о домашних и животных.

- Проблемы с едой: ученики решают задачи, связанные с едой, рисуя, чтобы выяснить, сколько всего было съедено печенья, пиццы, кексов.
- Задачи «Зимние забавы» используют снеговиков, чтобы вовлечь детский сад в решение задач.
- Самая большая сумма предлагает учащимся расположить заданные цифры, чтобы получить наибольшую сумму.
- Наименьшая сумма предлагает учащимся расположить заданные цифры так, чтобы получить наименьшую сумму.
- Наибольшая разница — бросает вызов учащимся, чтобы расположить указанные цифры так, чтобы получить наибольшую разницу.
- Наименьшая разница предлагает учащимся расположить указанные цифры так, чтобы разница была наименьшей.
- Bean Bags оценивает понимание учащимися значения разряда с использованием длинных чисел и кубов с основанием десять.
- Digit Game — 1 предлагает студентам составить как можно большее число, используя три цифры, которые вытащил каждый игрок. & nbsp Учащиеся должны определить победителя игры и объяснить, как они решили, кто победил.

- Digit Game — 2 похожа на Digit Game -2 и может использоваться для дополнительной практики.
- Ice Cream Treat касается комбинаций монет и внесения сдачи. Код
- Pizza Treat предназначен для совмещения монет и внесения сдачи.
- Quilt Square Challenge : Первоклассники школы Флинн в Перт-Амбой, штат Нью-Джерси, использовали блоки для квилтинга и коврики для квилтинга, чтобы воссоздать образцы блоков лоскутного одеяла 4×4 и 9×9. & nbsp См. «Quilt Square Challenge» на веб-странице Quilts, чтобы получить дополнительную информацию об этом упражнении и загрузить блоки и маты для учащихся.
- Образцы фигур: образцы фигур, которые заставляют учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.
- Class Gardens измеряет понимание учащимися территории и периметра.
- Модели роста рыб: Первоклассники школы Флинн в Перт-Амбой, штат Нью-Джерси, искали закономерности в растущей рыбе из книги Мэрилин Бернс по алгебраическому мышлению.
 & nbsp Учащиеся использовали блоки шаблонов для создания рыбок каждого возраста, организовали данные в виде Т-диаграммы, а затем на основе найденных ими шаблонов предсказали, что хотят более старые рыбы.
& nbsp Учащиеся использовали блоки шаблонов для создания рыбок каждого возраста, организовали данные в виде Т-диаграммы, а затем на основе найденных ими шаблонов предсказали, что хотят более старые рыбы. - Bay Street требует от учащихся проанализировать структуру номеров домов на Bay Street.Учащиеся записывают узор, который они видят, и используют этот числовой узор для записи отсутствующих номеров домов.
- King Street требует от учащихся проанализировать структуру номеров домов на King Street. Учащиеся записывают узор, который они видят, и используют этот числовой узор для записи отсутствующих номеров домов.
- Задачи по шаблонам: визуальные шаблоны, требующие от учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.
- Образцы фигур: образцы фигур, которые заставляют учащихся рисовать то, что будет дальше. & nbsp Учителя должны попросить учащихся объяснить, откуда они знают, что будет дальше, чтобы у учащихся развивалась способность объяснять свое мышление.

- «Зимние выкройки» для изучения выкройки используются снеговики, санки и рукавицы.
- Счет за минуту: Первоклассники в школе Флинн в Перте, Амбой, штат Нью-Джерси, использовали стикеры, чтобы нарисовать линейный график того, насколько высоко они могут считать за минуту.Затем учащиеся проанализировали данные, чтобы решить, насколько высоко может рассчитывать большинство первоклассников.
- Дни рождения требует, чтобы учащиеся интерпретировали данные в виде гистограммы.
- Fair Game оценивает понимание учащимися вероятности с помощью спиннеров.
- Четно-нечетная игра требует от учащихся интерпретировать данные в виде таблицы.
- «Любимые домашние животные» требует от учащихся проанализировать информацию в таблице подсчета любимых домашних животных.
- Любимое мороженое требует от учащихся проанализировать информацию в таблице подсчетов о шоколаде и ванильном мороженом.
- Pet Survey требует, чтобы учащиеся использовали данные в таблице частот, чтобы построить гистограмму и ответить на вопросы о ней.

- Сбор данных орла и решки требует от учащихся решить, является ли игра с подбрасыванием двух монет справедливой или нет, если один игрок выигрывает, если совпадают монеты (обе орла или оба решки), а другой игрок выигрывает, если монеты не совпадают (одна решка и одна решка).
- Конусы для мороженого: Учителя первого класса в школе Флинн в г. Перт-Амбой, штат Нью-Джерси, попросили учеников выяснить, сколько различных 3-мерных рожков мороженого они могут приготовить из шоколада, ванили и клубничного мороженого.Пары учащихся использовали вырезы из конусов и совков для сборки, а затем записали различные комбинации.
- Светофоры требуют от учащихся использовать метод упорядоченного подсчета, чтобы определить, сколько разных светофоров можно сделать, используя комбинацию красных, зеленых и желтых блоков. & nbsp Учащиеся могут использовать соединяющие кубы для моделирования светофоров и записывать комбинации, раскрашивая лист соответствующим образом.

Copyright © 2006-2010 — Терри Кавас — Все права защищены.
9 советов и приемов для решения задач со словами
Привет! Я Джо-Эллен из Love Believe Teach с Джо-Эллен Фуди, и я рада быть приглашенным блогером для Рэйчел Линетт.
Давайте поговорим о… проблемах со словами. Я могу начать с того, что скажу вам, что люблю учить детей решать словесные задачи, но не буду. Проблемы со словом сложны. Двухэтапные задачи со словами еще сложнее, и научить их решать, возможно, будет самым сложным навыком, которому вы обучаете в течение всего года. Хуже всего то, что вы ничего не можете с этим поделать. Неа! Нада! Задачи со словами есть в каждой математической программе, в каждом классе, в каждом стандартизированном математическом тесте, и они являются важным навыком, которым ученики должны овладеть, чтобы выжить в нашем мире.И это наша главная цель, верно?
Итак, вот что я обнаружил как наиболее полезный и наименее болезненный для учащихся способы научиться решать сложные словесные задачи.
Не ожидайте 100% мастерства после одного урока. Этого просто не произойдет. Я знаю, что это может быть трудно понять, но этот навык требует ВРЕМЕНИ и очень много. К сожалению, от этого никуда не деться.
Признайте, что задачи со словами сложны и вашим ученикам потребуется много практики с ними.По какой-то причине, сказав это вслух, весь процесс станет немного менее пугающим.
Используйте много, много, много форм практики. Я не могу этого достаточно подчеркнуть. Если у вас нет ученика, обладающего сверхспособностью решать задачи с чудодейственным словом, вашим ученикам понадобится ОЧЕНЬ много практики. Студентам нужны непосредственные инструкции всего класса, время с партнером, самостоятельные занятия для практики, веселые игры «вставай и двигайся», центры карточек с заданиями и домашние задания. Да, вам нужно привлечь родителей ваших учеников к тому, чтобы помочь их детям справиться с этими трудными проблемами.Разнообразие важно для того, чтобы ваши ученики продолжали практиковаться и улучшали свои навыки.
Обучайте, переучивайте, а затем, по прошествии некоторого времени, переучивайте снова. Иногда детям нужно время, чтобы усвоить все трюки, которым вы их научили. Поэтому после первого вводного урока подождите немного и повторите его с помощью короткого мини-урока, чтобы освежить их сознание. Повторяйте мини-уроки столько раз, сколько нужно.
Ох, ох! Я сказал это. И да, я имел это в виду.От этого никуда не деться. Судя по моему опыту (да, у меня его уже более 18 лет), студентам нужно много-много практики, чтобы справиться с задачами со словом. Иногда, просто иногда, может помочь решить проблему за проблемой. Вы можете мне не поверить, но для детей они действительно воспринимают это как вызов. Поверьте мне!
Вот как я это делаю: сначала я раздаю лист №1 с одной или двумя задачами. Я даю студентам время закончить, и как только они заканчивают, они проверяют его.Если они все поймут правильно, я немедленно даю им страницу №2. Затем я повторяю процесс снова и снова, пока не почувствую, что они устают. Вы узнаете, когда ваш класс достигнет дневного максимума. Они начнут отказываться от задания, работать не так усердно, «веселье» больше не витает в воздухе, и тогда я понимаю, что пора переходить к следующему занятию.
Вы узнаете, когда ваш класс достигнет дневного максимума. Они начнут отказываться от задания, работать не так усердно, «веселье» больше не витает в воздухе, и тогда я понимаю, что пора переходить к следующему занятию.
Другой способ попрактиковаться — превратить его в игру, чтобы увидеть, сколько задач класс может правильно решить за x минут. Начните со слов: «Мы собираемся отработать столько задач, сколько сможем за пять минут.На твоей отметке, готовься, ИДТИ! Ваш класс будет думать, что они играют в игру, а не решают сложные задачи со словами. Вы можете легко отслеживать, сколько задач класс решил правильно в установленные сроки. Если вы повторите эту игру несколько раз, вы увидите, что их общее количество становится все выше и выше по мере роста их навыков. Затем посмотрите, как ваш класс отмечает свои достижения. Они это заслужили!
Вот задача из двух слов БЕСПЛАТНО, чтобы помочь вашим ученикам начать практиковаться и практиковаться.Я считаю, что наиболее эффективно начинать с одной проблемы на странице, а учащиеся работают над тремя задачами на странице.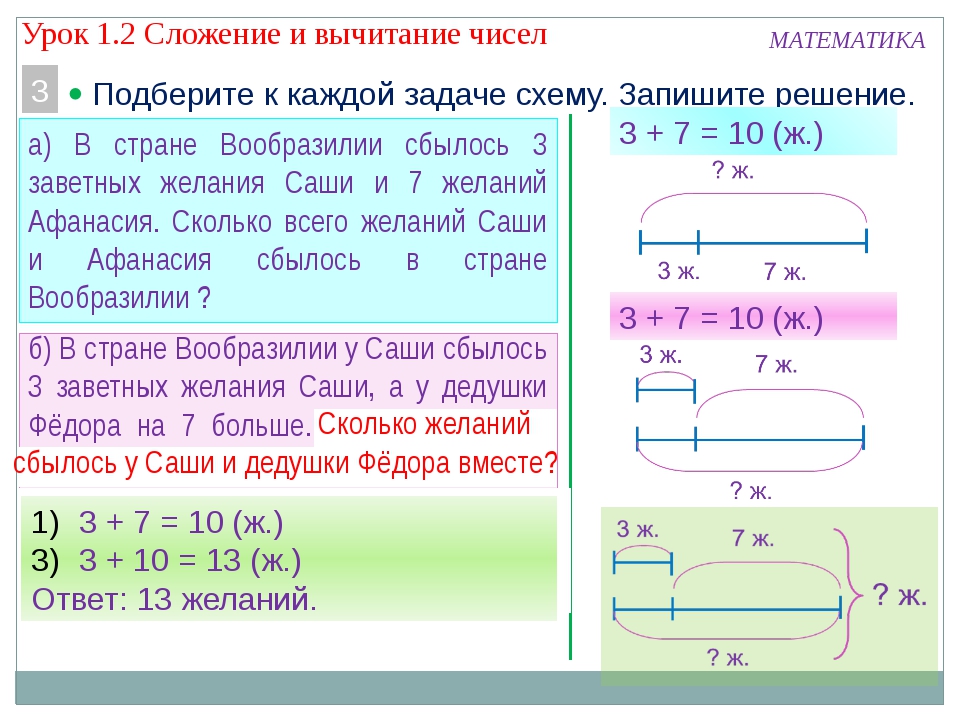
Да, некоторым детям они нужны. Им нужна система, которой нужно следовать. Я обнаружил, что дать студентам одну простую и понятную стратегию — лучший способ помочь этим студентам. Для них это просто не так запутанно. Убедитесь, что вы выбрали удачную стратегию!
Вот слово «план атаки», которое я использую со своими второклассниками:
- Шаг 1. Прочтите проблему и подумайте: «В чем проблема?»
- Шаг 2. Перечитайте проблему и подумайте: «В чем проблема?»
- Шаг 3. Спланируйте свою «атаку» и подумайте: «Как лучше всего решить эту проблему?»
- Шаг 4. Решите проблему и подумайте: «Какую операцию мне следует использовать?»
- Шаг 5: Проверьте свой ответ и подумайте: «Имеет ли мой ответ смысл? Моя математика верна? »
Да, мы учителя, и мы должны учить, но иногда дети просто не понимают, что мы говорим или как мы что-то объясняем.Это не делает нас плохими учителями; считайте это тайной юного ума. Все, что вам нужно сделать, это разделить на пары студентов, которые борются с кем-то, кто пытается справиться с проблемами. Прежде чем вы это узнаете, каждый с легкостью справится с этими проблемами со словами!
Прежде чем вы это узнаете, каждый с легкостью справится с этими проблемами со словами!
Попросите учащихся написать свои собственные задачи со словами, а затем попросите друга решить их. Как только ваши ученики научатся решать задачи со словами, вы увидите, как их понимание их будет расти.
Поговорите о том, что существует много разных способов решить проблему со словом, и что на 100% нормально решать проблему с помощью стратегии, отличной от другой.Примите эту идею и скажите своим ученикам, что все наши умы уникальны и решение этих проблем просто должно иметь смысл для вас.
Итак, вот и все. Я искренне надеюсь, что вы сможете найти несколько идей, которые сможете сразу же реализовать в своем собственном классе. Для большинства студентов проблемы со словами являются сложной задачей, но они никуда не денутся. Итак, давайте просто сделаем их чем-то, над чем мы будем работать вместе. Если у вас есть какие-либо советы и рекомендации, которые помогли вашим ученикам, я хотел бы услышать о них в комментариях ниже.
Джо-Эллен Фуди преподает более 18 лет в классах K-3. Она замужем, у нее двое маленьких мальчиков. Джо-Эллен увлечена мотивацией студентов выходить за рамки того, что они считали возможным. Ее магазин Teachers Pay Teachers называется Love Believe Teach with Jo-Ellen Foody и специализируется на классе K-3. Вы можете найти ее в Facebook, Instagram, Pinterest, Twitter или по электронной почте.
Урок второго класса Подсчет до решения задач
В начале урока я снова ввожу пустую числовую строку.Я даю каждому студенту пустую числовую строку на полосе предложений. Прошу сделать отметку прямо у левого края. Затем я приказываю им положить 2 пальца и сделать еще одну отметку. Я прошу их повторять это до тех пор, пока числовая строка не будет отмечена четными пробелами.
Затем я прошу их поставить цветную фишку на отметку у левого края. Я предлагаю им представить, что этот знак — число 18. Я прошу их использовать числовую линию, чтобы сосчитать 10 и найти на 10 больше, чем 18. Мы проверяем наши ответы. Теперь я прошу их переместить фишку на отметку в правом конце строки.Я прошу их представить, что это число 25. Я прошу их сосчитать 10 и найти 10 меньше 25.
Мы проверяем наши ответы. Теперь я прошу их переместить фишку на отметку в правом конце строки.Я прошу их представить, что это число 25. Я прошу их сосчитать 10 и найти 10 меньше 25.
Я повторяю это еще с несколькими числами. Я хочу усилить концепцию «на десять больше, на десять меньше» как способ понять сложение и вычитание десятков.
Затем я разбиваю класс на 3 группы, основываясь на их понимании числовой линии из неформальных оценок предыдущего урока.
Группе, которая может использовать числовую прямую для решения задач, выдается контрольный документ с задачами со словами, которые требуют сложения двухзначных чисел.Их просят работать вместе с партнерами или в одиночку, чтобы решать проблемы, используя свою цифровую линию, если это необходимо для поддержки их мышления.
Группа, которая имеет некоторое представление о числовой строке, но испытывает трудности с пустой строкой, будет работать с родителем, чтобы найти число в строке, а затем добавить к нему второе число. Здесь цель состоит в том, чтобы учащиеся поняли, что им не всегда нужно начинать с отметки на левом конце. Им нужно подумать о том, какое число они добавляют, то есть далеко ли оно от числа, с которого они начинают, или очень близко.Если он далеко, они должны считать по 2 или 10. Группа вместе примет некоторые решения об отправных точках, а затем решит проблемы.
Здесь цель состоит в том, чтобы учащиеся поняли, что им не всегда нужно начинать с отметки на левом конце. Им нужно подумать о том, какое число они добавляют, то есть далеко ли оно от числа, с которого они начинают, или очень близко.Если он далеко, они должны считать по 2 или 10. Группа вместе примет некоторые решения об отправных точках, а затем решит проблемы.
Группа, которая все еще не понимает, как работает числовая линия (они всегда хотят начинать с 1, даже если они ищут число 89), будет работать со мной, чтобы найти одно число относительно другого, считая единицы или Комбинации 2 и установка фишек на два числа. Если учащиеся овладеют этим навыком, мы попытаемся начать с однозначного числа и добавить второе однозначное число.
Задачи наслов для K-2 — Где происходит волшебство
Всем привет!
Обычно я получаю около 4 или 5 писем в неделю от учителей, которые купили мои ресурсы по задачам со словами для детского сада, 1-го и 2-го классов. Большинство вопросов, которые я получаю, связаны с учащимися, которым трудно понять, что им делать, когда они сталкиваются с ситуациями сложения и вычитания.
Большинство вопросов, которые я получаю, связаны с учащимися, которым трудно понять, что им делать, когда они сталкиваются с ситуациями сложения и вычитания.
Как я уже много раз говорил ранее, я не занимаюсь математикой. Собственно говоря, я был одним из тех студентов, которые ненавидели это из-за беспокойства по поводу математики.Я, однако, выполнил свою «домашнюю работу», не позволяя своим ученикам (и моим собственным мальчикам) дойти до этого момента, и сегодня я хочу предложить вам некоторое понимание.
Есть три основных уровня развития, когда дело доходит до решения проблем:
- Моделирование–> Прямое моделирование должно быть вашим шагом №1 в том, чтобы помочь вашим ученикам понять и развить чувство контекста и отношений при изучении того, как решать текстовые задачи. Я написал ЗДЕСЬ о том, как помочь студентам раскрыть взаимосвязь в задачах рассказа.Вы не можете ожидать, что ваши ученики будут использовать и применять какую-либо стратегию без предварительного моделирования.
 Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.
Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.
- Счетные стратегии -> Учащимся, которые используют счетные стратегии для решения сюжетных задач, вероятно, не нужно моделировать каждое число.Когда вы видите, что ваши ученики используют стратегии счета, они, вероятно, лучше осведомлены об отношениях в задаче рассказа. Некоторые из их стратегий подсчета можно придумать, а другие вам придется смоделировать в рамках своего руководства по стимуляции. Это несколько якорных диаграмм со стратегиями подсчета (сложение и вычитание), которые я составлял в прошлом со своими учениками.
- Полученные факты -> Хорошо, это этап, на котором ваши ученики действительно демонстрируют свои знания и беглость числовых фактов.
 Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.
Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.
Существует около 14-15 типов задач со словами. Некоторые из них труднее других, но к концу 2-го класса, когда дети познакомятся со всеми типами, они должны свободно владеть этими ситуациями сложения и вычитания.
На мой взгляд, сначала следует ввести словесные задачи «соединить» и «разделить». Их легче решить, потому что они включают реальные действия, которые дети могут смоделировать или разыграть.
Эти два типа задач со словами идеально подходят для введения и закрепления концепции «часть-часть-целое» с использованием числовых связей.
По опыту могу сказать: проблемы с неизвестным запуском и неизвестными изменениями всегда будут немного сложнее, чем другие. Это потому, что когда мои ученики готовятся к моделированию проблемы, они не знают, с чего начать… потому что начало неизвестно!
Задачи по части-части-целому — это очень весело. Я учил их, когда преподавал в первом классе пару лет назад, и мы обычно использовали их как возможность развить концептуальное понимание и составить комбинации.Также они идеально подходят для использования с Рекенрексом!
Самым сложным типом задач со словами для понимания для моих учеников было сравнение. Есть кое-что о формулировке и используемом языке:
- на
- меньше
- менее
- подробнее
- больше
- больше
Привет, словарь второго уровня!
Это особенно верно для изучающих английский язык и для студентов с плохим восприятием чисел и / или очень слабым языковым опытом.
Типовые задачи сравнения слов обеспечивают идеальный контекст для вас, чтобы представить и обучить стратегиям с использованием гистограмм. Я буду писать об этом позже.
Вы можете скачать шпаргалки по этим типам задач ЗДЕСЬ!
Пожалуйста, сделайте мне одолжение и не учите своих студентов решать задачи со словами, используя ключевые слова. Либо вы молодой учитель, либо опытный, не говорите своим ученикам, что «всего» означает прибавить, а «оставил» — вычесть. Я понимаю, что когда мы приближаемся к сезону тестирования, мы можем прибегнуть к этому, особенно если у нас есть ученики, которые все еще борются.Но, ради всего святого, это уводит от настоящего концептуального понимания, и мы лишь паршиво исправляем вещи.
Что он сказал.
Ключевые слова вводят в заблуждение… правда в том, что не во многих задачах-историях есть ключевые слова, и ваши ученики также не смогут решать многоступенчатые задачи со словами.
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ УЗНАТЬ О НАШИХ РЕСУРСАХ ПРОБЛЕМЫ WORD ДЛЯ ДЕТСКОГО САДА, ПЕРВОГО И ВТОРОГО КЛАССА.

Вы можете получить БЕСПЛАТНЫЙ образец моих задач со словом для первого и второго класса ЗДЕСЬ!
Вы также можете получить ПОЛНУЮ продукцию в моем магазине TPT.
Надеюсь, вам понравился этот пост, спасибо за внимание!
ТОРГОВЫЙ СПИСОК
Уровень 2 — Сводные данные по подразделениям
Раздел 1: монеты, числовые строки и задачи с рассказом (26 сеансов)Сложение, вычитание и система счисления 1
Этот модуль фокусируется на сложении и вычитании однозначных чисел, в частности, на сложении чисел в любом порядке; переход от счета по единицам к счету по группам, особенно по десяткам и единицам, что закладывает основу для работы учащихся с разметкой знаков и десятичной системой счисления; и разработка и уточнение стратегий для решения множества задач сложения и вычитания.Будучи первым блоком во 2-м классе, он также знакомит с математическими инструментами, процессами и способами работы, которые станут основой математического класса. В рамках этой работы студенты знакомятся с несколькими годичными учебными занятиями, которые предлагают регулярную практику по составлению и разложению чисел, разработке визуальных образов величин, фактов сложения и вычитания, определения времени, а также подсчета, сбора и анализа данных.
В рамках этой работы студенты знакомятся с несколькими годичными учебными занятиями, которые предлагают регулярную практику по составлению и разложению чисел, разработке визуальных образов величин, фактов сложения и вычитания, определения времени, а также подсчета, сбора и анализа данных.
- Исследование 1: Знакомство с математическими инструментами и рутинными занятиями (6 занятий)
- Расследование 2: Имеет ли значение порядок? (8 сеансов)
- Исследование 3: Сравнение количеств и подсчет по группам (7 сеансов)
- Исследование 4: Решение сюжетных задач (5 сеансов)
Геометрия и дроби
Основное внимание в этом модуле уделяется наблюдению и описанию определяющих атрибутов двумерных и трехмерных форм (например,g., количество и форма граней, количество и длина сторон, количество углов и вершин), а также использование этих атрибутов при сортировке, построении, рисовании и сравнении форм. Этот блок также развивает идеи о равных частях целого, уделяя особое внимание разделению и описанию половин, четвертей и третей одного целого и признавая, что одна и та же равная часть целого (например, одна половина квадрата) может иметь разные формы.
Этот блок также развивает идеи о равных частях целого, уделяя особое внимание разделению и описанию половин, четвертей и третей одного целого и признавая, что одна и та же равная часть целого (например, одна половина квадрата) может иметь разные формы.
- Исследование 1: Атрибуты двумерных и трехмерных фигур (5 сеансов)
- Исследование 2: Четырёхугольники, прямоугольники и квадраты (6 сеансов)
- Исследование 3: половины, четверти и трети (8 сеансов)
Этот блок фокусируется на разряде двухзначных чисел и работе с этими числами в пределах 100.Студенты приходят к выводу, что 100 — это десять десятков, а число, кратное 100, состоит из некоторого числа сотен. Они решают различные типы сюжетных задач (например, собрать / разобрать с одним или обоими неизвестными дополнениями, добавить и взять из с неизвестным результатом, проблемы с неизвестным изменением или неизвестным началом). Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операции.Студенты также определяют, читают и записывают числа до 500, а также мысленно складывают и вычитают 10 к числам в этом диапазоне.
Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операции.Студенты также определяют, читают и записывают числа до 500, а также мысленно складывают и вычитают 10 к числам в этом диапазоне.
- Исследование 1: Наклейка (8 сеансов)
- Исследование 2: Сложение и вычитание в течение 100 (9 сеансов)
- Исследование 3: Проблемы с неизвестным изменением или неизвестным началом (7 сеансов)
Моделирование с использованием данных
Этот модуль специализируется на сортировке и классификации категориальных данных; заказ числовых данных; и сбор и представление категориальных и числовых данных с использованием различных представлений: представления, созданные студентами, графические изображения, гистограммы, диаграммы Венна, кубические башни и линейные графики. Учащиеся описывают данные и обсуждают, что они говорят им об опрошенной группе. При этом учащиеся развивают способность моделировать на основе данных аспекты своего мира.
Учащиеся описывают данные и обсуждают, что они говорят им об опрошенной группе. При этом учащиеся развивают способность моделировать на основе данных аспекты своего мира.
- Исследование 1: Работа с категориальными данными (6 сеансов)
- Исследование 2: Работа с числовыми данными (6 сеансов)
Сложение, вычитание и система счисления 3
Этот блок фокусируется на разряде трехзначных чисел и оперирует числами в пределах 100.Студенты приходят к выводу, что 100 — это 10 десятков, а число, кратное 100, состоит из некоторого числа сотен. Они решают различные типы сюжетных задач (например, собрать / разобрать с одним или обоими неизвестными дополнениями, добавить и взять из с неизвестным результатом, проблемы с неизвестным изменением или неизвестным началом). Они играют в игры, в которых суммируются суммы, чтобы получить 100 или 1 доллар. Работа над быстрым сложением и вычитанием в пределах 100 продолжается с упором на использование известных фактов и знаний об операциях. Беглость с суммированием в пределах 100 является эталоном для этого устройства. Учащиеся также определяют, читают и записывают числа до 1000, а также складывают и вычитают 10 и 100 к числам в этом диапазоне.
Беглость с суммированием в пределах 100 является эталоном для этого устройства. Учащиеся также определяют, читают и записывают числа до 1000, а также складывают и вычитают 10 и 100 к числам в этом диапазоне.
- Исследование 1: 100 комбинаций (6 сеансов)
- Исследование 2: Сложение в пределах 100 и подсчет до 1000 (6 сеансов)
- Исследование 3: Свободное владение в пределах 100 (8 занятий)
Линейное измерение
Этот модуль специализируется на разработке стратегий точного измерения длины с помощью нестандартных и стандартных единиц (например,g., ремесленные палки, кубы, дюймы, футы, ярды, сантиметры и метры) и инструменты (например, измерительные инструменты для дюймового кирпича, линейки, мерки и метры), а также для рассмотрения взаимосвязи между различными единицами измерения и инструментами (например, , чем больше единица, тем меньше будет счетчик). Учащиеся представляют данные измерений на линейном графике, а также решают сюжетные задачи, которые включают сложение, вычитание и сравнение длин.
Учащиеся представляют данные измерений на линейном графике, а также решают сюжетные задачи, которые включают сложение, вычитание и сравнение длин.
- Исследование 1: Земля дюйма (6 сеансов)
- Исследование 2: две системы измерения (6 сеансов)
Основы умножения
Основное внимание в этом модуле уделяется работе с равными группами как основе умножения, исследуя четные и нечетные числа и представляя равные группы с помощью массивов и таблиц.
- Исследование 1: четное или нечетное? (4 сеанса)
- Исследование 2: Исследование равных групп (6 занятий)
Сложение, вычитание и система счисления 4
Этот блок фокусируется на развитии и достижении беглости с помощью вычитания в пределах 100, а также на достижении беглости с фактами сложения и вычитания в пределах 20, над которыми студенты работали в течение года.


 )
)

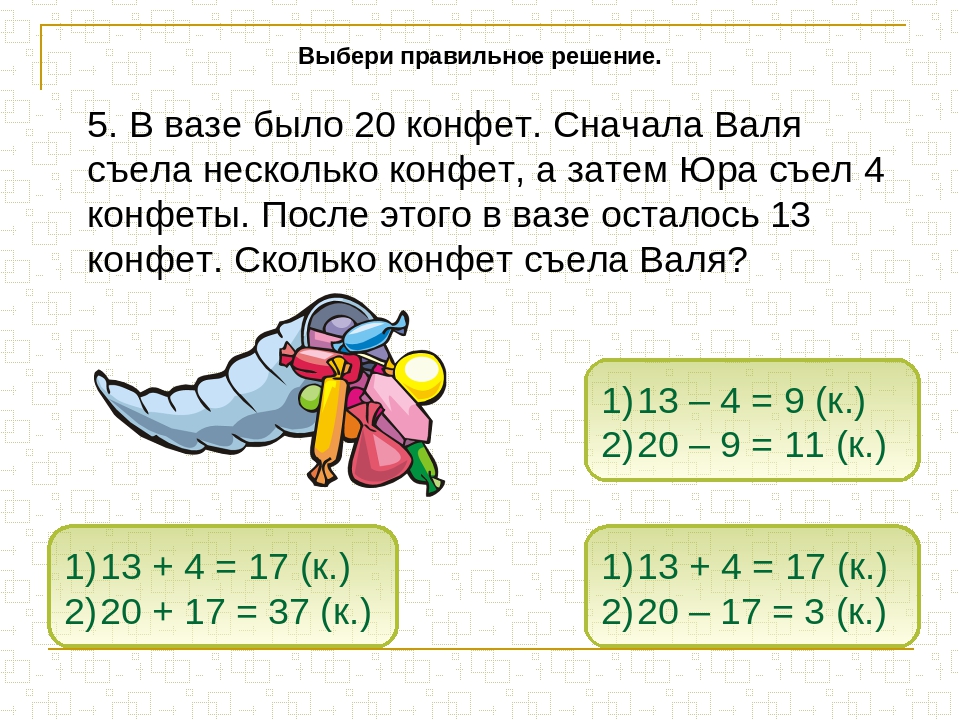 Мама помыла 6 тарелок, а Оля помыла 3 чашки. Сколько всего вымыто посуды?
Мама помыла 6 тарелок, а Оля помыла 3 чашки. Сколько всего вымыто посуды? Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
Определите, кажется ли ваш ответ разумным. Если возможно, сравните свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.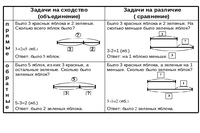


 & nbsp Учащиеся использовали блоки шаблонов для создания рыбок каждого возраста, организовали данные в виде Т-диаграммы, а затем на основе найденных ими шаблонов предсказали, что хотят более старые рыбы.
& nbsp Учащиеся использовали блоки шаблонов для создания рыбок каждого возраста, организовали данные в виде Т-диаграммы, а затем на основе найденных ими шаблонов предсказали, что хотят более старые рыбы.
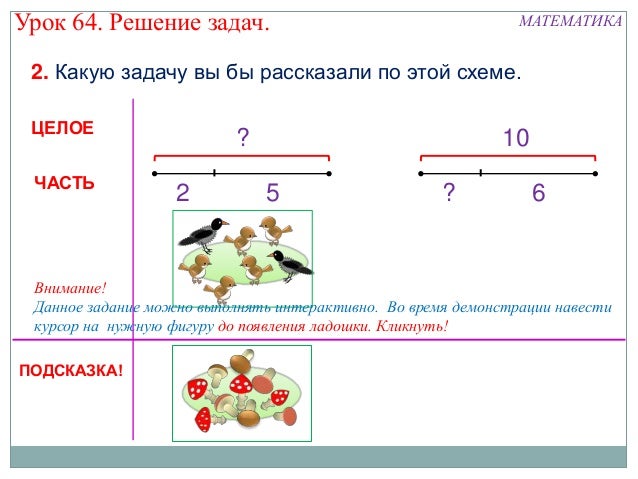

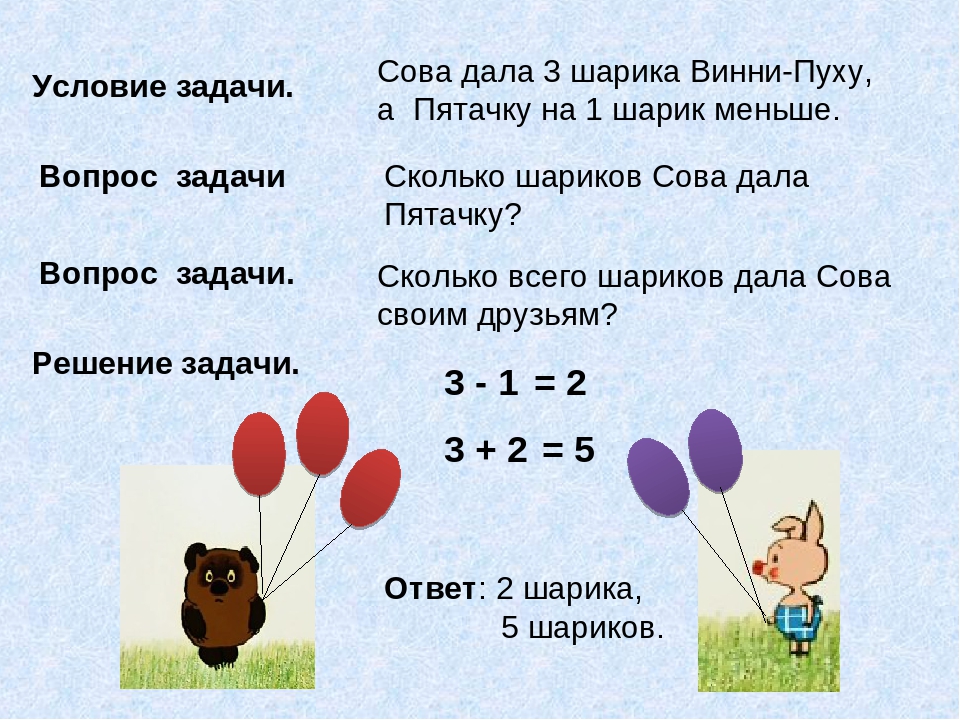 Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов.
Позвольте детям использовать свои пальцы, если они находятся в K или 1st, или даже если они недостаточно знакомы с ситуациями сложения и вычитания. Им понадобится МНОГО возможностей, чтобы взаимодействовать, слушать, терпеть неудачу и добиваться успеха. Некоторые стратегии моделирования: использование пальцев, рисунков или использование реальных объектов. Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.
Обычно я могу сказать, когда мои ученики составляют и раскладывают числа, компенсируют их, ищут способы использовать контрольные числа. и т.д. Я написал ЗДЕСЬ о контрольных цифрах. С другой стороны, на этом этапе студенты уже занимаются вычислениями. И с вычислениями приходит потребность решить. Иногда это стремление решать и вычислять может отвлекать наших студентов от осмысления и анализа проблемы рассказа. Когда вы начнете наблюдать это, вы можете попробовать убрать цифры из слов «проблемы». Таким образом, у них нет другого выбора, кроме как разобраться в контексте и отношениях.