Сложение и вычитание чисел от 1 до 10 — онлайн тренажер — Kid-mama
Для того, чтобы научиться быстро и правильно считать, нужно решать много примеров. И для этого одних занятий в школе и выполнения домашнего задания мало. Нужны дополнительные средства обучения.
К сожалению, приобрести или распечатать специальные рабочие тетради или книги не у всех есть возможность, а хороших бесплатных онлайн тренажеров в интернете найти практически невозможно.Поэтому мы создали для вас онлайн игру — математический тренажер для тренировки устного счета в пределах десяти. В этом тренажере 100 примеров, некоторые из которых повторяются несколько раз. Как правило это примеры на сложение и вычитание, наиболее часто вызывающие затруднения.
Благодаря работе с тренажером происходит автоматизация и повышается скорость счета. В данном тренажере примеры расположены от более простых к более сложным и разбиты на 4 группы. Решать все 100 примеров за один раз не нужно. Следующий раз вы сможете начать решать с 25, 50 или 75 примера.
Наш тренажер «Сложение и вычитание чисел от 1 до 10» рассчитан на первоклассников, но заниматься на нем могут и дошкольники. Удобство тренажера в том, что переход к следующему примеру происходит автоматически, сразу, как только вы нажмете правильный ответ, нет кнопок «Проверить» и «дальше», которые при большом количестве слайдов нажимать обычно утомительно. При этом происходит подсчет правильных и неправильных нажатий.
Еще одно преимущество нашего онлайн тренажера — кнопки расположены прямо на игровом поле, и не нужно уводить взгляд на клавиатуру. Мы надеемся, что с нашим онлайн тренажером занятия математикой превратятся в интересную и увлекательную игру.
Примеры в тренажере достаточно простые, если вам нужен тренажер посложнее, работайте с тренажером №2, в котором примеры немного сложнее.
При работе с математическими тренажерами не только повышается скорость счета, но и развивается внимание, усидчивость, улучшается оперативная память.
Перейти на страницу с тренажером
Учимся решать примеры до 10.
Ваш ребенок уже знает цифры, может отыскать названную вслух цифру, а также отвечает, как называется цифра, которую вы показываете? Не откладывайте обучение счету, решайте примеры вместе со своим малышом. Ниже несколько примеров в пределах 10.
Чтобы проверить, правильно ли ребенок соотносит цифру и количество предметов, которые она обозначает, попросим малыша выполнить задание.
Положите на стол 2 небольших предмета — например, пуговки. Спросите, сколько пуговок на столе? Попросите малыша показать столько пальчиков на руке, сколько предметов на столе, между делом потренируем и мелкую моторику. Добавьте 1 пуговку, спросите, сколько стало? Далее будем добавлять пуговки по одной в достаточно быстром темпе, проговаривая результат – фактически называя цифры по-порядку. Дойдя до десяти, начинаем убирать пуговки по одной. Здесь уже поможем малышу – будем называть результат вместе, одновременно изучая обратный счет. Поясните, что добавляя пуговки, мы совершаем действие – сложение, обозначаем это действие знаком плюс, а убирая – вычитание, и его обозначаем минусом. Знание прямого и обратного счета, умение посчитать от любого числа вперед и обратно, пригодится в решении примеров.
Наглядно прямой и обратный счет можно показать с помощью лесенки, она – наш помощник в счете.
Чтобы решить пример: 3 + 1, малышу надо пальчиком встать на третью ступеньку, а затем сделать 1 шаг вверх. Ответом на пример будет ступенька, на которой он окажется. Для решения примера 5 – 2 мы встаем на пятую ступеньку и делаем 2 шага вниз. Спросите у ребенка – если в примере знак плюс, надо подниматься или опускаться по нашей лесенке? Какой знак написан в примере, если я шагаю вниз? Если прибавляем или отнимаем ноль, надо ли делать шаги, или почему «шагнув на ноль ступенек вверх или вниз» мы остаемся на месте? Почаще играйте так с малышом, с опорой на зрительную память он хорошо запомнит лесенку. Совсем скоро он легко будет решать примеры, даже не имея подсказки-лесенки перед глазами.
Начните с простых шагов и обязательно занимайтесь регулярно, чтобы ребенок хорошенько усвоил принцип решения. Не забудьте выполнять упражения на сложение и вычитание на IQsha! Затем можно будет усложнять задания, предлагая решать простые примеры в уме.
Счет в пределах 10 для детей от 5-6 лет
Здесь мы подготовили для вас математические примеры — Счет в пределах 10 — для максимальной тренировки детей, готовящихся к поступлению в школу или уже учащихся в 1-2 классах. Скачайте примеры во вложениях, распечатайте все листы на принтере и попросите ребенка решить примеры, объяснив ему условия.
Математические примеры — Счет в пределах 10 на скорость:
Примеры нужно решать на скорость. Каждый лист поделен на 2 части — правая и левая половины. Для каждой части внизу даны пустые клетки, в которых нужно вписать время, за которое ребенок решил все примеры этой половины листа. Справа от клеток вы увидите оценку результатов ребенка. Если ребенок затратил на выполнение задания более 4 минут, то его оценка — грустный смайлик, если он успел правильно решить примеры менее, чем за 4 минуты — улыбающийся смайлик. Ну а если он справился менее, чем за 3 минуты — смайлик очень радостный — это высшая оценка!
Математические примеры — Счет в пределах 10 в количестве 8 страниц (то есть 16 заданий), находятся во вложениях внизу страницы.








Похожие задания, обучающие счету до 10, вы можете найти и в других материалах:
 Счет до 10 для детей дошкольного возраста
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.

Считаем до 20 с помощью веселых игровых заданий для распечатки! Все, что вам нужно — это выбрать любой набор задачек в картинках, скачать их во вложениях и распечатать на принтере.
 Устный счет в пределах 10 — Картинки с заданиями
Устный счет в пределах 10 — Картинки с заданиями
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
 Раскраски с заданиями на счет в пределах 10
Раскраски с заданиями на счет в пределах 10
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями. Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.

В этих интересных заданиях дети узнают, что такое порядковый счет до 10. А те, кто уже знакомы с этим понятием, могут показать свои знания с помощью данного упражнения.
 Счет до 5 — Картинки с заданиями для малышей
Счет до 5 — Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
 Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи
Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также в развивающих математических играх от лисенка Бибуши:
 Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
 Игра «Найди числа на картинке» для малышей от 4 лет
Игра «Найди числа на картинке» для малышей от 4 лет
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
 Математическая игра «Найди наибольшее и наименьшее число»
Математическая игра «Найди наибольшее и наименьшее число»
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое. После правильного ответа он услышит порядковый счет до этого числа.
 Игра «Сложение и вычитание до 10» — Задачки в картинках
Игра «Сложение и вычитание до 10» — Задачки в картинках
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши, в которой малыш сможет решить восемь новых задачек на счет до 10.
 Задачи-примеры для малышей в картинках
Задачи-примеры для малышей в картинках
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10. В трех уровнях игры ребенок будет решать задачи на вычитание, а в пяти — складывать заданные предметы.
Математическая игра — Примеры на вычитание до 10 — Падающие яблоки
Математическая игра «Примеры на вычитание до 10 — Падающие яблоки» разработана для детей от 5 лет. Здесь ребенок должен проверить свое умение решать примеры на вычитание в пределах 10. Также игра пригодится дошкольникам, которые готовятся к школе и постепенно осваивают математические азы. Математическая игра сделана яркой и красочной, чтобы детям было интересно, а учеба не казалась скучной.
Математическая игра на вычитание до 10 — Посчитай яблоки
В игре даны 10 примеров на вычитание до 10. Ребенок должен прослушать пример и нажать на соответствующее число, которое и будет являться ответом. После этого начнут падать с дерева яблоки. Яблок упадет ровно столько, сколько указано в вычитаемом. Например, если дан пример «10 — 4 =», то упадет 4 яблока, а 6 останутся на дереве. Затем оставшиеся яблоки будут пересчитаны с озвучкой — чтобы ребенок понимал, что ответ примера совпадает с количеством оставшихся яблок.
Если ребенку тяжело решать пример в числовом варианте, пусть пересчитывает яблоки, прежде чем нажимать на ответ (нужно пересчитать все яблоки, а затем отнять столько яблок, сколько указано в вычитаемом.

Математическая игра «Примеры на вычитание до 10»
Если игра загружается не до конца — обновите страницу!
Очень полезны для изучения математики наши задания для распечатки:
Математика в картинках — Задания для распечатки
Здесь вы можете скачать и распечатать множество заданий в картинках по математике, которые проверят навыки и умения ребенка считать, прибавлять, отнимать, делить предметы поровну, использовать математические знаки для сравнения чисел и многое другое…
Впиши математические знаки и символы
На этой странице вы сможете найти самые разнообразные задания в картинках, где основная задача состоит в умении ребенка ставить математические знаки и символы между числами.
Примеры на сложение до 10 «Умный паровозик»
Главная / Математические игры для детей
Сегодня мы подготовили для тебя математическую игру «Умный паровозик» — Примеры на сложение до 10. Эта игра предназначена для детей старшего дошкольного и младшего школьного возраста. Игра поделена на 2 задания. В первом задании ребенку нужно составлять примеры из вагончиков, а во втором задании — решать примеры и выбирать правильный ответ на воздушных шариках.
- В первом задании ребенок должен составлять примеры из вагончиков. На кабине паровозика написано число — номер паровозика. Это число является суммой, которая должна получиться, если пример из вагончиков составлен правильно. Ребенок должен перетаскивать вагончики с нужными числами и ставить их рядом с кабиной паровоза. В итоге у ребенка должен получиться правильный пример из вагончиков. Если пример составлен верно, то паровозик поедет, а следом за ним приедет следующий паровозик с другим номером.
- Во втором задании нужно решать примеры на паровозике, который едет по мосту. А ответ нужно выбирать на воздушных шариках. Только учтите, что время ограничено! Решить пример и выбрать правильный ответ нужно успеть до того, как паровозик скроется из виду. Внимание! Во втором задании засчитываются ошибки за неправильные ответы.

Математическая игра «Умный паровозик» — Примеры на сложение до 10
Рекомендованные материалы:
Добавить комментарий
Тесты онлайн по математике для 1 класса
Здесь выложены онлайн тесты по математике, в которых ребенок сможет решить задачи для 1 класса, а также выполнить задания на сложение и вычитание.
Математические задачи составлены с учетом школьной программы для 1 класса. В задачах представлены действия на сложение и вычитание однозначных чисел: 5+3, 8-4, 2+2, и действия на сложение и вычитание двузначных чисел с однозначными: 10 + 7, 17 – 7, 17 – 10.
Среди представленных тестов есть задачи для 1 класса, как с одним действием, так и с двумя действиями. Конечно же, сначала ребенку нужно потренировать свои математические способности в задачах с одним действием. А когда уже ребенок сможет решать их легко — смело переходите к более сложным задачам в два действия. Главное — чтобы обучение шло по нарастающей, тогда результат будет гораздо выше и эффективнее.
Для любого ребенка задачи всегда сложнее, чем примеры. Так как в них нужно не только решить пример, но и составить этот пример на основе заданного условия. А для этого уже требуется логическое и образное мышление.
Тесты на сложение и вычитание отлично тренируют математические способности ребенка и его умение считать в уме. Чем чаще ребенок будет тренироваться, тем выше будет его успеваемость в школе. Тесты составлены на основе того, что должен знать и уметь ребенок в 1 классе. Сюда входит: Числа от 1 до 10, Нумерация чисел, Сложение и вычитание от 0 до 10 и от 10 до 20, Сравнение чисел, Единица времени: час, Единицы длины: сантиметр, дециметр, Соотношение между ними, Единица массы: килограмм, Единица вместимости: литр, Знаки + (плюс), – (минус), = (равно), Названия компонентов и результатов сложения и вычитания (их использование при чтении и записи числовых выражений).
А теперь можете по порядку проходить все онлайн тесты по математике для 1 класса. Будьте внимательны!
Тесты
Здесь вы должны решить математические задачи на нахождение суммы для 1 класса. В тесте — 10 вопросов-задач
Здесь вы должны решить математические задачи на нахождение суммы для 1 класса, 2 часть. В тесте — 10 вопросов-задач
Здесь вы должны пройти математические задачи на нахождение суммы для 1 класса, 3 часть. В тесте — 10 вопросов-задач
Здесь вы должны пройти математические задачи на нахождение остатка для 1 класса. В тесте — 10 вопросов-задач
Здесь вы должны решить математические задачи на нахождение остатка для 1 класса, 2 часть. В тесте — 10 вопросов-задач
Математические игры — Онлайн Бесплатно!
Математические игры — Онлайн Бесплатно!- игры на 2
- стрелялки
- симулятор
- головоломки
- гонки
- io
- стратегии
- майнкрафт
- тесты
- гта
- поиск предметов
- танки
- огонь и вода
- бродилки
- марио
- рисовалки
- когама
- футбол
- зомби
- ферма
- аниме
- снайпер
- одевалки
- раскраски
- пазлы
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
Введите полиномиальное неравенство вместе с переменной, для которой необходимо решить, и нажмите кнопку «Решить».
В главе 2 мы установили правила решения уравнений с использованием чисел в арифметике. Теперь, когда мы изучили операции с числами со знаком, мы будем использовать те же правила для решения уравнений, содержащих отрицательные числа. Мы также изучим методы решения и построения графиков неравенств с одним неизвестным.
РЕШЕНИЕ УРАВНЕНИЙ НА ЗАПИСАННЫХ ЧИСЛАХ
ЗАДАЧИ
По завершении этого раздела вы сможете решать уравнения, содержащие числа со знаком.
Пример 1 Решите относительно x и проверьте: x + 5 = 3
Решение
Используя те же процедуры, что и в главе 2, мы вычитаем 5 из каждой части уравнения, получая
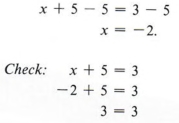
Пример 2 Решите относительно x и проверьте: — 3x = 12
Решение
Разделив каждую сторону на -3, получаем
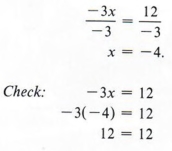
| Всегда проверяйте исходное уравнение. |

| Другой способ решения уравнения 3x — 4 = 7x + 8 — сначала вычесть 3x из обеих сторон, получив -4 = 4x + 8, , затем вычесть 8 с обеих сторон и получить -12 = 4x . Теперь разделите обе стороны на 4, получив — 3 = x или x = — 3. |

| Сначала удалите круглые скобки. Затем следуйте процедуре, описанной в главе 2. |
ЛИТЕРАЛЬНЫЕ УРАВНЕНИЯ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите буквальное уравнение.
- Примените ранее изученные правила для решения буквальных уравнений.
Уравнение, содержащее более одной буквы, иногда называют буквальным уравнением . Иногда бывает необходимо решить такое уравнение для одной из букв через другие. Пошаговая процедура, описанная и использованная в главе 2, остается действительной после удаления любых символов группировки.
Пример 1 Решить относительно c: 3 (x + c) — 4y = 2x — 5c
Решение
Сначала удалите круглые скобки.
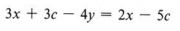
Здесь мы отмечаем, что, поскольку мы решаем для c, мы хотим получить c с одной стороны и все другие члены с другой стороны уравнения. Таким образом, получаем
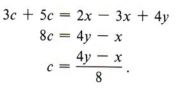

| Помните, abx — это то же самое, что 1abx. Делим на коэффициент при x, который в данном случае равен ab. |

| Решите уравнение 2x + 2y — 9x + 9a, сначала вычтя 2.v с обеих сторон. Сравните полученное решение с полученным в примере. |
Иногда форму ответа можно изменить. В этом примере мы могли бы умножить числитель и знаменатель ответа на (- l) (это не меняет значения ответа) и получить
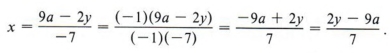
Преимущество этого последнего выражения перед первым в том, что в ответе не так много отрицательных знаков.
| Умножение числителя и знаменателя дроби на одно и то же число является использованием фундаментального принципа дробей. |
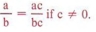
Наиболее часто используемые буквальные выражения — это формулы из геометрии, физики, бизнеса, электроники и т. Д.
Пример 4 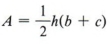 — это формула для площади трапеции. Решите для c.
— это формула для площади трапеции. Решите для c.
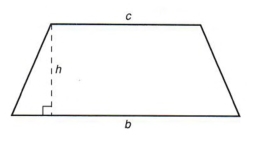

| Трапеция имеет две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями. Удаление скобок не означает их простое стирание. Мы должны умножить каждый член в круглых скобках на коэффициент, стоящий перед скобками. Изменять форму ответа не обязательно, но вы должны уметь распознавать правильный ответ, даже если форма не та. |
Пример 5 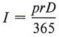 — это формула, дающая проценты (I), полученные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда известны сумма процентов, основная сумма и количество дней.
— это формула, дающая проценты (I), полученные за период D дней, когда известны основная сумма (p) и годовая ставка (r). Найдите годовую ставку, когда известны сумма процентов, основная сумма и количество дней.
Решение
Задача требует решения 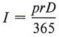 для р.
для р.
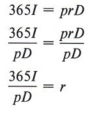
Обратите внимание, что в этом примере r оставлено с правой стороны, и поэтому вычисление было проще. При желании мы можем переписать ответ по-другому.
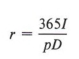
ГРАФИЧЕСКИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Используйте символ неравенства, чтобы обозначить относительное положение двух чисел в числовой строке.
- График неравенств на числовой прямой.
Мы уже обсуждали набор рациональных чисел как числа, которые могут быть выражены как отношение двух целых чисел. Также существует набор чисел, называемых иррациональными числами , , которые нельзя выразить как отношение целых чисел. В этот набор входят такие номера, как 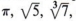 и так далее. Набор, состоящий из рациональных и иррациональных чисел, называется действительными числами.
и так далее. Набор, состоящий из рациональных и иррациональных чисел, называется действительными числами.
Для любых двух действительных чисел a и b всегда можно сказать, что 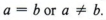 Часто нас интересует только то, равны ли два числа или нет, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Часто нас интересует только то, равны ли два числа или нет, но бывают ситуации, когда мы также хотим представить относительный размер чисел, которые не равный.
Символы представляют собой символы неравенства или отношения порядка и используются для отображения относительных размеров значений двух чисел. Обычно мы читаем символ как «больше чем». Например, a> b читается как «a больше, чем b». Обратите внимание: мы заявили, что обычно читаем
а

| Какое положительное число можно добавить к 2, чтобы получить 5? |

Проще говоря, это определение утверждает, что a меньше b, если мы должны что-то добавить к a, чтобы получить b.Конечно, «что-то» должно быть положительным.
Если вы думаете о числовой прямой, вы знаете, что добавление положительного числа эквивалентно перемещению вправо по числовой прямой. Это приводит к следующему альтернативному определению, которое может быть легче визуализировать.
Пример 1 3

| Мы также можем написать 6> 3. |
Пример 2 -4

| Мы также можем написать 0> — 4. |
Пример 3 4> — 2, потому что 4 находится справа от -2 в числовой строке.

Пример 4 — 6

Математическое утверждение x
| Вы понимаете, почему невозможно найти наибольшее число меньше 3? |
На самом деле, назвать число x, которое является наибольшим числом меньше 3, невозможно. Однако это может быть указано в числовой строке.Для этого нам нужен символ, обозначающий значение такого оператора, как x
Символы (и), используемые в числовой строке, указывают на то, что конечная точка не включена в набор.
Пример 5 График x
Решение

Обратите внимание, что на графике есть стрелка, указывающая на то, что линия продолжается без конца влево.
| На этом графике представлено каждое действительное число меньше 3. |
Пример 6 График x> 4 на числовой прямой.
Решение

| На этом графике представлены все действительные числа больше 4. |
Пример 7 График x> -5 на числовой прямой.
Решение

| На этом графике представлены все действительные числа больше -5. |
Пример 8 Постройте числовой график, показывающий, что x> — 1 и x
Решение

Выписка x> — 1 и x
| На этом графике представлены все действительные числа от -1 до 5. |
Пример 9 График — 3
Решение

Если мы хотим включить конечную точку в набор, мы используем другой символ, 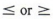 :. Мы читаем эти символы как «равно или меньше» и «равно или больше».
:. Мы читаем эти символы как «равно или меньше» и «равно или больше».
Пример 10 x>; 4 указывает число 4 и все действительные числа справа от 4 в числовой строке.
Символы [и] в числовой строке указывают, что конечная точка включена в набор.
| Вы обнаружите, что такое использование круглых и квадратных скобок согласуется с их использованием в будущих курсах математики. |

| На этом графике представлено число 1 и все действительные числа больше 1. |
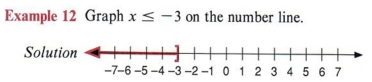
| На этом графике представлено число 1 и все действительные числа, меньшие или равные — 3. |
Пример 13 Напишите алгебраическое утверждение, представленное следующим графиком.

Пример 14 Напишите алгебраическое выражение для следующего графика.
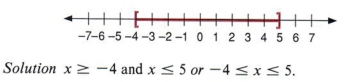
| На этом графике представлены все действительные числа от -4 до 5 , включая от -4 до 5. |
Пример 15 Напишите алгебраическое выражение для следующего графика.
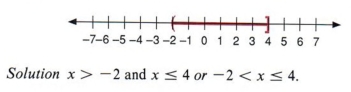
| Этот график включает 4, но не -2. |
Пример 16 График 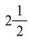 на числовой прямой.
на числовой прямой.
Решение
В этом примере возникает небольшая проблема. Как мы можем указать в числовой строке 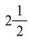 ? Если мы оценим суть дела, то другой человек может неправильно истолковать это утверждение. Не могли бы вы сказать, представляет ли точка
? Если мы оценим суть дела, то другой человек может неправильно истолковать это утверждение. Не могли бы вы сказать, представляет ли точка 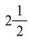 или, может быть,
или, может быть, 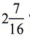 ? Поскольку цель графика — пояснить, всегда обозначает конечную точку .
? Поскольку цель графика — пояснить, всегда обозначает конечную точку .
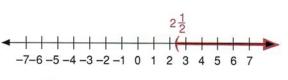
| График используется для передачи утверждения. Вы всегда должны называть нулевую точку, чтобы показать направление, а также конечную точку или точки, если быть точным. |
УСТРАНЕНИЕ НЕРАВЕНСТВА
ЗАДАЧИ
По завершении этого раздела вы сможете решить неравенства с одним неизвестным.
Решение неравенств обычно включает те же основные правила, что и уравнения. Есть одно исключение, которое мы скоро обнаружим. Однако первое правило аналогично тому, что используется при решении уравнений.
Если одинаковое количество добавляется к каждой стороне неравенства , результаты будут неравными в том же порядке.
Пример 1 Если 5
Пример 2 Если 7
Мы можем использовать это правило для решения некоторых неравенств.
Пример 3 Решить относительно x: x + 6
Решение
Если мы прибавим -6 к каждой стороне, мы получим
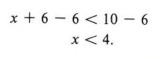
Изобразив это решение на числовой прямой, получим


| Обратите внимание, что процедура такая же, как и при решении уравнений. |
Теперь мы воспользуемся правилом сложения, чтобы проиллюстрировать важную концепцию, касающуюся умножения или деления неравенств.
Предположим, что x> a.
Теперь добавьте — x к обеим сторонам по правилу сложения.
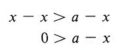
| Помните, добавление одинаковой величины к обеим сторонам неравенства не меняет его направления. |
Теперь добавьте -a с обеих сторон.
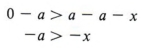
Последний оператор — a> -x можно переписать как — x <-a.Поэтому мы можем сказать: «Если x> a, то — x
Если неравенство умножается или делится на отрицательное число , результаты будут неравными в порядке , противоположном .
| Например: Если 5> 3, то -5 |
Пример 5 Решите относительно x и изобразите решение: -2x> 6
Решение
Чтобы получить x в левой части, мы должны разделить каждый член на — 2. Обратите внимание, что, поскольку мы делим на отрицательное число, мы должны изменить направление неравенства.
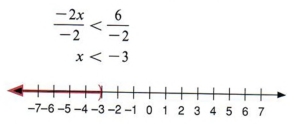
| Обратите внимание, что как только мы делим на отрицательную величину, мы должны изменить направление неравенства. |
Обратите особое внимание на этот факт. Каждый раз, когда вы делите или умножаете на отрицательное число, вы должны изменять направление символа неравенства. Это единственное различие между решением уравнений и решением неравенств.
| Когда мы умножаем или делим на положительное число, изменений нет.Когда мы умножаем или делим на отрицательное число, направление неравенства меняется. Будьте осторожны — это источник многих ошибок. |
После того как мы удалили круглые скобки и остались только отдельные члены в выражении, процедура поиска решения почти такая же, как в главе 2.
Давайте теперь рассмотрим пошаговый метод из главы 2 и отметим разницу при решении неравенств.
Первый Исключите дроби, умножив все члены на наименьший общий знаменатель всех дробей.(Без изменений, когда мы умножаем на положительное число.)
Второй Упростите, объединив одинаковые члены с каждой стороны неравенства. (Без изменений)
Третий Сложите или вычтите количества, чтобы получить неизвестное с одной стороны и числа с другой. (Без изменений)
Четвертый Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет отменено.(Это важное различие между уравнениями и неравенствами.)
| Единственное возможное различие — это последний шаг. |

| Что нужно делать при делении на отрицательное число? |

| Не забудьте пометить конечную точку. |
РЕЗЮМЕ
Ключевые слова
- Буквенное уравнение — это уравнение, состоящее из более чем одной буквы.
- Символы — это символы неравенства или отношения порядка .
- a a находится слева от b в строке действительного числа.
- Двойные символы
 : указывают, что конечные точки включены в набор решений .
: указывают, что конечные точки включены в набор решений .
Процедуры
- Чтобы решить буквальное уравнение для одной буквы через другие, выполните те же шаги, что и в главе 2.
- Чтобы решить неравенство, используйте следующие шаги:
Шаг 1 Исключите дроби, умножив все члены на наименьший общий знаменатель всех дробей.
Шаг 2 Упростите, объединив одинаковые члены с каждой стороны неравенства.
Шаг 3 Сложите или вычтите величины, чтобы получить неизвестное с одной стороны и числа с другой.
Шаг 4 Разделите каждый член неравенства на коэффициент неизвестной. Если коэффициент положительный, неравенство останется прежним. Если коэффициент отрицательный, неравенство будет отменено.
Шаг 5 Проверьте свой ответ.
Решайте неравенства с помощью программы «Пошаговое решение математических задач»
Введите уравнение вместе с переменной, для которой вы хотите его решить, и нажмите кнопку «Решить».
В этой главе мы разработаем определенные методы, которые помогут решить проблемы, сформулированные на словах. Эти методы включают переписывание задач в виде символов. Например, заявленная проблема
«Найдите число, которое при добавлении к 3 дает 7»
можно записать как:
3+? = 7, 3 + n = 7, 3 + x = 1
и так далее, где символы?, N и x представляют собой число, которое мы хотим найти.Мы называем такие сокращенные версии поставленных задач уравнениями или символическими предложениями. Такие уравнения, как x + 3 = 7, являются уравнениями первой степени, поскольку переменная имеет показатель степени 1. Члены слева от знака равенства составляют левую часть уравнения; те, что справа, составляют правую часть. Таким образом, в уравнении x + 3 = 7 левый член равен x + 3, а правый член равен 7.
РЕШЕНИЕ УРАВНЕНИЙ
Уравнения могут быть истинными или ложными, так же как предложения слов могут быть истинными или ложными.Уравнение:
3 + х = 7
будет ложным, если вместо переменной подставлено любое число, кроме 4. Значение переменной, для которой верно уравнение (4 в этом примере), называется решением уравнения. Мы можем определить, является ли данное число решением данного уравнения, подставив число вместо переменной и определив истинность или ложность результата.
Пример 1 Определите, является ли значение 3 решением уравнения
4x — 2 = 3x + 1
Решение Мы заменяем значение 3 на x в уравнении и смотрим, равен ли левый член правому.
4 (3) — 2 = 3 (3) + 1
12 — 2 = 9 + 1
10 = 10
Отв. 3 — решение.
Уравнения первой степени, которые мы рассматриваем в этой главе, имеют не более одного решения. Решения многих таких уравнений можно определить путем осмотра.
Пример 2 Найдите решение каждого уравнения путем осмотра.
а. х + 5 = 12
б. 4 · х = -20
Решения а. 7 — решение, так как 7 + 5 = 12.
b. -5 — это решение, поскольку 4 (-5) = -20.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВ СЛОЖЕНИЯ И ВЫЧИТАНИЯ
В разделе 3.1 мы решили несколько простых уравнений первой степени путем проверки. Однако решения большинства уравнений не сразу видны при осмотре. Следовательно, нам необходимы некоторые математические «инструменты» для решения уравнений.
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
Эквивалентные уравнения — это уравнения, которые имеют идентичные решения. Таким образом,
3x + 3 = x + 13, 3x = x + 10, 2x = 10 и x = 5
эквивалентны уравнениям, потому что 5 — единственное решение каждого из них.Обратите внимание, что в уравнении 3x + 3 = x + 13 решение 5 не очевидно при осмотре, но в уравнении x = 5 решение 5 очевидно при осмотре. Решая любое уравнение, мы преобразуем данное уравнение, решение которого может быть неочевидным, в эквивалентное уравнение, решение которого легко заметить.
Следующее свойство, иногда называемое свойством сложения-вычитания , является одним из способов создания эквивалентных уравнений.
Если одинаковое количество прибавляется или вычитается из обоих элементов уравнения, полученное уравнение эквивалентно исходному уравнение.
в символах,
a — b, a + c = b + c и a — c = b — c
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
х + 3 = 7
путем вычитания 3 из каждого члена.
Решение Если вычесть 3 из каждого члена, получим
х + 3 — 3 = 7 — 3
или
х = 4
Обратите внимание, что x + 3 = 7 и x = 4 являются эквивалентными уравнениями, поскольку решение одинаково для обоих, а именно 4.В следующем примере показано, как мы можем генерировать эквивалентные уравнения, сначала упростив один или оба члена уравнения.
Пример 2 Напишите уравнение, эквивалентное
4x- 2-3x = 4 + 6
, объединив одинаковые термины, а затем добавив по 2 к каждому члену.
Объединение одинаковых терминов дает
х — 2 = 10
Добавление 2 к каждому члену дает
х-2 + 2 = 10 + 2
х = 12
Чтобы решить уравнение, мы используем свойство сложения-вычитания, чтобы преобразовать данное уравнение в эквивалентное уравнение вида x = a, из которого мы можем найти решение путем проверки.
Пример 3 Решите 2x + 1 = x — 2.
Мы хотим получить эквивалентное уравнение, в котором все члены, содержащие x, находятся в одном члене, а все члены, не содержащие x, — в другом. Если мы сначала прибавим -1 к каждому члену (или вычтем 1 из него), мы получим
2x + 1-1 = x — 2-1
2x = х — 3
Если мы теперь прибавим -x к каждому члену (или вычтем x из него), мы получим
2х-х = х — 3 — х
х = -3
, где решение -3 очевидно.
Решением исходного уравнения является число -3; однако ответ часто отображается в виде уравнения x = -3.
Поскольку каждое уравнение, полученное в процессе, эквивалентно исходному уравнению, -3 также является решением 2x + 1 = x — 2. В приведенном выше примере мы можем проверить решение, подставив — 3 вместо x в исходном уравнении.
2 (-3) + 1 = (-3) — 2
-5 = -5
Симметричное свойство равенства также помогает при решении уравнений. В этом объекте указано
Если a = b, то b = a
Это позволяет нам менять местами члены уравнения в любое время, не беспокоясь о каких-либо изменениях знака.Таким образом,
Если 4 = x + 2, то x + 2 = 4
Если x + 3 = 2x — 5, то 2x — 5 = x + 3
Если d = rt, то rt = d
Может быть несколько разных способов применить свойство сложения, указанное выше. Иногда один метод лучше другого, а в некоторых случаях также полезно симметричное свойство равенства.
Пример 4 Решите 2x = 3x — 9. (1)
Решение Если мы сначала добавим -3x к каждому члену, мы получим
2x — 3x = 3x — 9 — 3x
-x = -9
, где переменная имеет отрицательный коэффициент.Хотя при осмотре мы можем видеть, что решением является 9, поскольку — (9) = -9, мы можем избежать отрицательного коэффициента, добавив -2x и +9 к каждому члену уравнения (1). В этом случае получаем
2x-2x + 9 = 3x- 9-2x + 9
9 = х
, из которого решение 9 очевидно. При желании мы можем записать последнее уравнение как x = 9 по симметричному свойству равенства.
РЕШЕНИЕ УРАВНЕНИЙ С ИСПОЛЬЗОВАНИЕМ СВОЙСТВА DIVISION
Рассмотрим уравнение
3x = 12
Решение этого уравнения — 4.Также обратите внимание, что если мы разделим каждый член уравнения на 3, мы получим уравнения
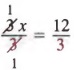
, решение которого также равно 4. В общем, мы имеем следующее свойство, которое иногда называют свойством деления.
Если оба члена уравнения делятся на одно и то же (ненулевое) количество, полученное уравнение эквивалентно исходному уравнению.
в символах,
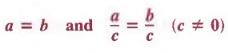
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
-4x = 12
, разделив каждый член на -4.
Решение Разделив оба элемента на -4, получим
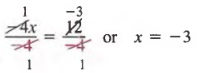
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, в которых переменная имеет коэффициент 1.
Пример 2 Решите 3y + 2y = 20.
Сначала мы объединяем похожие термины, чтобы получить
5лет = 20
Тогда, разделив каждый член на 5, получим
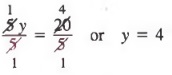
В следующем примере мы используем свойство сложения-вычитания и свойство деления для решения уравнения.
Пример 3 Решить 4x + 7 = x — 2.
РешениеСначала мы добавляем -x и -7 к каждому члену, чтобы получить
4x + 7 — x — 7 = x — 2 — x — 1
Далее, объединяя одинаковые термины, получаем
3x = -9
Наконец, мы разделим каждый член на 3, чтобы получить
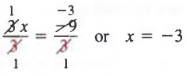
РЕШЕНИЕ УРАВНЕНИЙ С СВОЙСТВОМ УМНОЖЕНИЯ
Рассмотрим уравнение
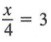
Решение этого уравнения — 12. Также обратите внимание, что если мы умножим каждый член уравнения на 4, мы получим уравнения
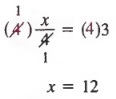
, решение которого также равно 12.В общем, мы имеем следующее свойство, которое иногда называют свойством умножения.
Если оба члена уравнения умножаются на одну и ту же ненулевую величину, полученное уравнение эквивалентно исходному уравнению.
в символах,
a = b и a · c = b · c (c ≠ 0)
— эквивалентные уравнения.
Пример 1 Напишите уравнение, эквивалентное
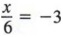
путем умножения каждого члена на 6.
Решение Умножение каждого члена на 6 дает
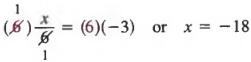
При решении уравнений мы используем указанное выше свойство для создания эквивалентных уравнений, не содержащих дробей.
Пример 2 Решить 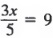
Решение Сначала умножьте каждый член на 5, чтобы получить
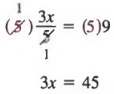
Теперь разделите каждого члена на 3,
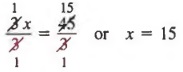
Пример 3 Решить 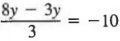 .
.
Решение Во-первых, упростите над дробной чертой, чтобы получить
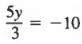
Затем умножьте каждый член на 3, чтобы получить
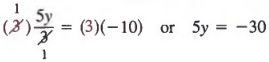
Наконец, разделив каждого члена на 5, получим
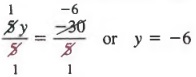
ДАЛЬНЕЙШИЕ РЕШЕНИЯ УРАВНЕНИЙ
Теперь мы знаем все методы, необходимые для решения большинства уравнений первой степени.Не существует определенного порядка, в котором следует применять свойства. Может оказаться подходящим любой один или несколько из следующих шагов, перечисленных на странице 102.
Шаги по решению уравнений первой степени:
- Объедините одинаковые члены в каждом члене уравнения.
- Используя свойство сложения или вычитания, запишите уравнение со всеми членами, содержащими неизвестное в одном члене, и всеми членами, не содержащими неизвестное в другом.
- Объедините одинаковые термины в каждом элементе.
- Используйте свойство умножения для удаления дробей.
- Используйте свойство деления, чтобы получить коэффициент 1 для переменной.
Пример 1 Решите 5x — 7 = 2x — 4x + 14.
Решение Сначала мы объединяем одинаковые члены, 2x — 4x, чтобы получить
5x — 7 = -2x + 14
Затем мы добавляем + 2x и +7 к каждому члену и объединяем одинаковые термины, чтобы получить
5x — 7 + 2x + 7 = -2x + 14 + 2x + 1
7x = 21
Наконец, мы разделим каждый член на 7, чтобы получить

В следующем примере мы упрощаем над полосой дроби перед применением свойств, которые мы изучали.
Пример 2 Решить 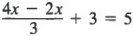
Решение Во-первых, мы объединяем одинаковые термины, 4x — 2x, чтобы получить
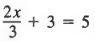
Затем мы добавляем -3 к каждому члену и упрощаем
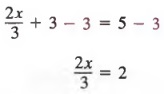
Затем мы умножаем каждый член на 3, чтобы получить

Наконец, мы делим каждый член на 2, чтобы получить
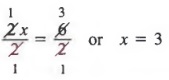
РЕШЕНИЕ ФОРМУЛ
Уравнения, в которых используются переменные для измерения двух или более физических величин, называются формулами.Мы можем найти любую одну из переменных в формуле, если известны значения других переменных. Мы подставляем известные значения в формулу и решаем неизвестную переменную методами, которые мы использовали в предыдущих разделах.
Пример 1 В формуле d = rt найти t, если d = 24 и r = 3.
Решение Мы можем найти t, заменив 24 на d и 3 на r. То есть
d = rt
(24) = (3) т
8 = т
Часто бывает необходимо решить формулы или уравнения, в которых существует более одной переменной для одной из переменных в терминах других.Мы используем те же методы, что и в предыдущих разделах.
Пример 2 В формуле d = rt найдите t через r и d.
Решение Мы можем решить для t в терминах r и d, разделив оба члена на r, чтобы получить
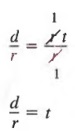
из которых по закону симметрии
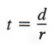
В приведенном выше примере мы решили для t, применив свойство деления для создания эквивалентного уравнения. Иногда необходимо применить более одного такого свойства.
Пример 3 В уравнении ax + b = c решите относительно x через a, b и c.
Решение Мы можем решить для x, сначала добавив -b к каждому члену, чтобы получить
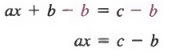
, затем разделив каждый член на a, мы получим
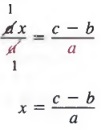
8 проблем онлайн-обучения и способы их решения
Мир образования и обучения движется в сторону онлайн-обучения. Преимущества неоспоримы: снижение затрат, большая гибкость для студентов и возможность обучать тысячи людей по всему миру одновременно. Кроме того, вы можете следить за тем, что студенты делают в любой момент, и это нарушает инерцию и пассивность учебных курсов.
Однако электронное обучение не лишено недостатков.Онлайн-обучение имеет свои особенности, которые могут поставить под угрозу (или ограничить) успех обучения. Электронное обучение не следует рассматривать как панацею. Только зная проблемы, с которыми столкнулись другие компании и учреждения, вы можете реализовать программы, чтобы полностью реализовать свой потенциал.
Таким образом, в этой статье мы выделили 8 основных проблем онлайн-обучения. Но не волнуйтесь, мы нашли решение для всех них.
Проблема 1. Онлайн-обучение — это скучно
Хотя онлайн-обучение призвано избавить от скуки обучения в классе, это не всегда так.Многие курсы электронного обучения состоят из бесконечных текстов, за которыми следует длинный список вопросов с несколькими вариантами ответов, которые не привлекают студентов. Это больше, чем электронное обучение, это похоже на электронное чтение.
Курсы такого типа означают, что студентам часто наскучивает онлайн-обучение, и это отсутствие заинтересованности и мотивации является одной из основных причин неудач электронных курсов. Студенты просто не заинтересованы в обучении, не имеют доступа к платформе и не завершают курс. МООК (массовые открытые онлайн-курсы) являются хорошим примером: только 10% студентов, которые зарегистрировались на курс, действительно его заканчивают.
Решение: Найдите интерактивный курс, который будет динамичным, увлекательным и интерактивным.
Чтобы учащимся не было скучно, обязательно найдите интерактивный, динамичный и увлекательный интерактивный курс. Хотя в первые дни электронного обучения это могло быть сложно, в настоящее время это намного проще: в настоящее время существует ряд провайдеров, предлагающих все виды интерактивного обучения, с задачами и приключениями, видео, рассказыванием историй, игровыми решениями, симуляторами для обеспечения практика и обучение на основе игр.


А если вы хотите добавить дополнительную мотивацию к обучению, вы можете предложить другие стимулы. Опыт показал, например, что когда студенты получают официальную квалификацию или сертификат в конце курса, они становятся более вовлеченными в обучение. Вы также можете продвигать соревнование, добавляя рейтинги, классификации и призы для победителей (денежные или другие вознаграждения). Все это повысит вовлеченность сотрудников, и участники не только с большей вероятностью закончат курс, но, прежде всего, узнают больше и лучше.
Задача 2: Студенты сталкиваются с техническими трудностями
Хотя это может показаться очевидным, технические проблемы являются одним из основных камней преткновения при онлайн-обучении. Очень часто возникают проблемы с совместимостью (с операционными системами, браузерами или смартфонами), курсы никогда не сдвигаются с мертвой точки или студент не знает, как продолжить. Все это усугубляет их разочарование и снижает вовлеченность сотрудников, процесс обучения нарушается, и они, вероятно, откажутся от курса.
Решение: предлагайте курсы с несколькими устройствами и личное внимание
Столкнувшись с этой проблемой, не усложняйте ее. Выбирайте онлайн-курсы, которые не требуют много внутренней памяти или высокоскоростного подключения к Интернету, а также имеют надежный и простой сценарий. Отдавайте приоритет курсам, где вам не нужно загружать какие-либо программы или распечатывать документы. Когда вы проходите обучение перед учениками, обратите внимание на качество звука (проблема, которой часто пренебрегают), и обязательно опробуйте курс на нескольких смартфонах, браузерах и операционных системах.
Кроме того, выбирайте онлайн-курсы с простой и исчерпывающей справочной страницей, подробным разделом часто задаваемых вопросов и отличными услугами по уходу за студентами. Если в онлайн-курсе есть чат, адрес электронной почты или форум для устранения технических неполадок, вы можете быть уверены, что технологии не будут проблемой и не будут мешать процессу обучения.
Проблема 3: студенты не знают, что курс существует
Это часто случается: вы потратили месяцы на подготовку онлайн-курса, вы выбрали лучшего провайдера, вы знаете, что курс важен для ваших сотрудников … но никого организация знает о ее существовании.В распоряжении студентов есть сотни и тысячи курсов, и они часто перегружены работой и повседневной рутиной. В результате никто не знает, о чем идет речь, и, следовательно, не принимает его.
Решение: Запустите коммуникационную кампанию
Если вы хотите, чтобы ученики действительно обращали на вас внимание, подумайте о том, чтобы рассматривать запуск любого учебного плана как премьеру голливудского фильма. Проведите презентацию в самом большом конференц-зале компании (не могли бы вы показать трейлер или превью онлайн-курса? Выступит ли генеральный директор с речью?).Создайте предвкушение, используя цепочку электронных писем или разместите большие плакаты по всему офису (например, с надписью «Требуются» или «Скоро будут»). Все это вызовет интерес студентов, а вы создадите ажиотаж еще до начала обучения. Обязательно объясните, почему обучение важно для сотрудников и как оно поможет им стать лучшими профессионалами и лучшими людьми.
При этом не забудьте проинформировать начальство и всех начальников отделов о тренинге. Основываясь на опыте различных организаций, онлайн-курсы работают намного лучше, если вы можете привлечь к работе старших сотрудников компании.Старшие сотрудники не только имеют возможность предоставить членам своей команды время для посещения тренинга, но также могут подавать пример и, следовательно, поощрять сотрудников нижнего уровня организации к прохождению курсов.
Задача 4: У студентов нет времени на онлайн-обучение
Формат электронного обучения предлагает студентам большую гибкость: они могут посещать курсы в любое время и в любом месте, в своем собственном темпе и без физических ограничений. Однако такая гибкость часто приводит к бездействию.Проходит время, а студент все еще не получил доступ к платформе обучения и не прошел курс. У них так много времени и гибкости … что они никогда не могут найти время для этого.
Решение: установите лимит времени и отправьте напоминания
Чтобы решить эту проблему, во-первых, убедитесь, что курсы разделены на несколько частей и состоят из коротких уроков, которые можно пройти за короткий промежуток времени. Если учащиеся сталкиваются с серьезными препятствиями на пути к обучению, они, вероятно, никогда не найдут времени, чтобы их решить.Разделите курсы и побеждайте.
Во-вторых, не бойтесь устанавливать временные рамки. Тот факт, что обучение проходит в режиме онлайн, не означает, что вы не можете установить сроки. Составьте четкий и простой календарь, указывающий, когда студент должен завершить каждую часть онлайн-курса. Кроме того, разошлите студентам напоминания о том, что у них не хватает времени, и побудите их завершить курс.
Задача 5: Студентам необходимо общаться с людьми
Онлайн-курсы имеют множество преимуществ, но мы также должны осознавать их ограничения.Студенты иногда могут расстраиваться из-за отсутствия человеческого контакта, отсутствия учителя и неспособности обсудить это со своими одноклассниками. Иногда онлайн-мир, каким бы богатым он ни был, может стать слишком маленьким для учащегося, и ему может потребоваться физическое пространство, где он сможет решать свои вопросы и практиковаться с помощью реальных инструментов.
Решение: личное внимание, форумы и социальные сети
Если это проблема, одно из решений — как можно больше способствовать личному взаимодействию в онлайн-мире.Вы можете организовать веб-семинары, групповую работу или форумы, где студенты могут обсудить и решить свои вопросы. Очень важно, чтобы у учащихся был учитель, с которым они могли бы связаться (например, обучение по Skype). Вы также можете продвигать использование социальных сетей во время обучения, тем самым предоставляя дополнительную возможность для социального взаимодействия и гуманизируя процесс обучения.
Еще одно решение — совместить онлайн-курсы с некоторыми видами обучения в классе. Было продемонстрировано, что этот тип смешанного обучения (известный как смешанное обучение) усиливает то, что студенты узнали, и повышает образовательную ценность обучения.Таким образом, до, во время или после курса вы можете организовать дебаты между студентами или занятия с учителем. Таким образом, вы смешаете онлайн и офлайн миры и преодолеете одно из самых очевидных ограничений электронного обучения.
Задача 6: Студенты не могут практиковать
Наука показала, что лучший способ чему-то научиться — это практиковать это (знаменитая концепция обучения на практике). Только практикуя то, что мы делаем и переживаем (экспериментальное обучение), мы можем усвоить и вспомнить содержание и навыки, которые мы изучаем.Однако многие онлайн-курсы упускают из виду эту часть и сосредотачиваются исключительно на теоретическом содержании и внешних уроках. В результате студенты не могут практиковаться, и процесс обучения не раскрывает весь свой потенциал.
Решение: используйте полезные и практические курсы с тренажёрами.
Чтобы студенты могли практиковаться, необходимо, чтобы курсы были полезными и практичными. Сотрудники должны чувствовать (даже если эгоистично), что обучение будет полезно им в их повседневной работе и поможет им стать лучшими профессионалами (и, по сути, людьми).Если курсы электронного обучения будут соответствовать этому требованию, студенты смогут применить все, что они узнают, на практике в реальном мире.
Кроме того, чтобы они могли практиковаться во время онлайн-курса, вам следует использовать тренажеры. Симуляторы использовались десятилетиями (например, пилотами и хирургами) для воссоздания реальных жизненных ситуаций, чтобы студенты могли практиковаться и экспериментировать в безопасной и контролируемой среде. Если вы включите тренажеры в свой учебный курс, вы сможете решить эту проблему и убедиться, что ваши ученики применяют свои новые знания и навыки на практике.
Проблема 7: Качество курсов посредственное
Студенты мотивированы, содержание курса звучит интересно, была запущена коммуникационная кампания, так что все об этом знают … но так уж получилось, что качество содержания не повышается по номиналу В условиях информационной перегрузки современного мира, наличия тысяч бесплатных онлайн-курсов и таких мощных платформ, как Википедия, YouTube и Google, содержание курсов должно быть превосходным и соответствовать высочайшим стандартам. Тем не менее, многие студенты разочаровываются, когда обнаруживают, что могут узнать больше самостоятельно, чем на простых посредственных курсах, предлагаемых их компаниями или учреждениями.
Решение: предлагайте только лучшее
За последние годы мир сильно изменился, и ваша работа тоже. Одна из ваших самых важных задач как человека, ответственного за обучение, — это найти, выбрать лучшие курсы и определить их приоритетность. Помните: вы должны быть лучше Google. Так что выбирайте только самое лучшее.
Проблема 8: Онлайн-курс не влияет на вашу организацию
Иногда электронное обучение может решить все вышеперечисленные проблемы.Студенты получили доступ к учебной платформе, у них не возникло никаких технических проблем, они завершили курс в установленные сроки и смогли применить на практике то, что узнали. Однако какое влияние обучение оказало на вашу организацию? Улучшил ли это человеческий капитал вашей компании? У вас есть результаты, которые вы можете показать начальству? Многие проекты электронного обучения терпят неудачу по той простой причине, что они не повлияли на организацию в целом.
Решение: согласовать онлайн-курсы с целями вашей организации (и измерить их!)
Лучший способ решить эту проблему — спланировать обучение до начала.Вы должны четко понимать свои цели обучения и почему вы хотите, чтобы ваши студенты проходили именно этот онлайн-курс. Самое главное, чтобы обучение соответствовало интересам вашей компании или учреждения. Поэтому вам следует выбирать материалы, которые действительно будут способствовать достижению общих целей организации (например, увеличение продаж компании, повышение осведомленности персонала по конкретному вопросу или улучшение управления обслуживанием клиентов).
Более того, обязательно измеряйте результаты обучения.Установите индикаторы перед реализацией проекта и вернитесь и измерьте их снова после завершения курса. Таким образом, вы узнаете, какое влияние обучение оказало на вашу организацию. Если вы не измеряете его, как вы узнаете, был ли курс успешным или неудачным? Эти цифры позволят вам оценить, что сработало, а что нет, и оправдают инвестиции для вашего начальства.
.основ машинного обучения с алгоритмом K-ближайших соседей | by Onel Harrison

Алгоритм k-ближайших соседей (KNN) — это простой, легко реализуемый алгоритм контролируемого машинного обучения, который можно использовать для решения задач как классификации, так и регрессии. Пауза! Давайте распакуем это.
ABC. Мы делаем это очень просто!Алгоритм машинного обучения с учителем (в отличие от алгоритма машинного обучения без учителя) — это алгоритм, который полагается на помеченные входные данные для изучения функции, которая производит соответствующий результат при получении новых немаркированных данных.
Представьте, что компьютер — это ребенок, мы — его руководитель (например, родитель, опекун или учитель), и мы хотим, чтобы ребенок (компьютер) узнал, как выглядит свинья. Мы покажем ребенку несколько разных картинок, некоторые из которых — это свиньи, а остальные могут быть изображениями чего угодно (кошек, собак и т. Д.).
Когда мы видим свинью, мы кричим «свинья!» Когда это не свинья, мы кричим: «Нет, не свинья!» Проделав это с ребенком несколько раз, мы показываем ему картинку и спрашиваем: «Свинья?» и они будут правильно (в большинстве случаев) сказать «свинья!» или «нет, не свинья!» в зависимости от того, что на картинке.Это машинное обучение с учителем.
«Свинья!»Алгоритмы машинного обучения с учителем используются для решения задач классификации или регрессии.
Задача классификации имеет дискретное значение на выходе. Например, «любит ананас на пицце» и «не любит ананас на пицце» дискретны. Там нет никакого среднего. Вышеупомянутая аналогия с обучением ребенка распознавать свинью — еще один пример проблемы классификации.
Изображение, показывающее случайно сгенерированные данныеНа этом изображении показан базовый пример того, как могут выглядеть данные классификации.У нас есть предиктор (или набор предикторов) и метка. На изображении мы, возможно, пытаемся предсказать, любит ли кто-то ананас (1) в пицце или нет (0), в зависимости от его возраста (предсказатель).
Стандартной практикой является представление вывода (метки) алгоритма классификации в виде целого числа, такого как 1, -1 или 0. В этом случае эти числа являются чисто репрезентативными. Математические операции над ними не должны выполняться, потому что это было бы бессмысленно. Задумайтесь на минутку.Что значит «любит ананас» + «не любит ананас»? Именно. Мы не можем добавлять их, поэтому мы не должны добавлять их числовые представления.
Задача регрессии имеет действительное число (число с десятичной точкой) в качестве выходных данных. Например, мы могли бы использовать данные в таблице ниже, чтобы оценить вес человека с учетом его роста.
Изображение, показывающее часть набора данных высоты и весов SOCR.Данные, используемые в регрессионном анализе, будут похожи на данные, показанные на изображении выше.У нас есть независимая переменная (или набор независимых переменных) и зависимая переменная (то, что мы пытаемся угадать с учетом наших независимых переменных). Например, мы могли бы сказать, что рост является независимой переменной, а вес — зависимой переменной.
Кроме того, каждая строка обычно называется примером , наблюдением или точкой данных , а каждый столбец (не включая метку / зависимую переменную) часто называется предиктором , измерением, независимой переменной или характеристикой.
Алгоритм неконтролируемого машинного обучения использует входные данные без каких-либо меток — другими словами, учитель (метка) не сообщает ребенку (компьютеру), когда он прав или когда он сделал ошибку, чтобы он мог сам -верный.
В отличие от обучения с учителем, которое пытается изучить функцию, которая позволит нам делать прогнозы с учетом некоторых новых немаркированных данных, обучение без учителя пытается изучить базовую структуру данных, чтобы дать нам более глубокое понимание данных.
Алгоритм KNN предполагает, что похожие объекты существуют в непосредственной близости. Другими словами, похожие вещи находятся рядом друг с другом.
Изображение, показывающее, как похожие точки данных обычно существуют близко друг к другу.«Птицы стая падают вместе».
Обратите внимание на изображение выше, что большую часть времени похожие точки данных расположены близко друг к другу. Алгоритм KNN зависит от того, насколько верно это предположение, чтобы алгоритм был полезен. KNN улавливает идею сходства (иногда называемого расстоянием, близостью или близостью) с некоторой математикой, которую мы, возможно, усвоили в детстве, — вычислением расстояния между точками на графике.
Примечание: Прежде чем двигаться дальше, необходимо понять, как мы рассчитываем расстояние между точками на графике. Если вы не знакомы с этим расчетом или нуждаетесь в нем заново, полностью прочтите « Расстояние между 2 точками » и сразу же вернитесь.
Есть и другие способы расчета расстояния, и один из них может быть предпочтительнее в зависимости от решаемой проблемы. Однако расстояние по прямой (также называемое евклидовым расстоянием) — популярный и знакомый выбор.
Алгоритм KNN
- Загрузить данные
- Инициализировать K для выбранного количества соседей
3. Для каждого примера в данных
3.1 Вычислить расстояние между примером запроса и текущим примером по данным.
3.2 Добавьте расстояние и индекс примера в упорядоченную коллекцию
4. Отсортируйте упорядоченную совокупность расстояний и индексов от наименьшего к наибольшему (в порядке возрастания) по расстояниям
5.Выберите первые K записей из отсортированной коллекции
6. Получите метки выбранных K записей
7. В случае регрессии верните среднее значение K меток
8. При классификации верните режим K меток
Реализация KNN (с нуля)
Выбор правильного значения для K
Чтобы выбрать K, который подходит для ваших данных, мы запускаем алгоритм KNN несколько раз с разными значениями K и выбираем K, который уменьшает количество ошибок с которыми мы сталкиваемся, сохраняя способность алгоритма точно делать прогнозы, когда ему предоставляются данные, которых он раньше не видел.
Вот некоторые вещи, о которых следует помнить:
- По мере того, как мы уменьшаем значение K до 1, наши прогнозы становятся менее стабильными. Подумайте на минуту, представьте, что K = 1 и у нас есть точка запроса, окруженная несколькими красными и одним зеленым (я думаю о верхнем левом углу цветного графика выше), но зеленый — единственный ближайший сосед. Разумно, мы могли бы подумать, что точка запроса, скорее всего, красная, но поскольку K = 1, KNN неправильно предсказывает, что точка запроса зеленая.
- И наоборот, когда мы увеличиваем значение K, наши прогнозы становятся более стабильными из-за большинства голосов / усреднения и, следовательно, с большей вероятностью будут делать более точные прогнозы (до определенного момента).В конце концов, мы начинаем замечать все большее количество ошибок. Именно в этот момент мы знаем, что зашли слишком далеко в значении K.
- В тех случаях, когда мы принимаем большинство голосов (например, выбираем режим в задаче классификации) среди меток, мы обычно делаем K нечетным числом, чтобы иметь возможность разрешения конфликтов.
Преимущества
- Алгоритм прост и удобен в реализации.
- Нет необходимости строить модель, настраивать несколько параметров или делать дополнительные предположения.
- Алгоритм универсален. Его можно использовать для классификации, регрессии и поиска (как мы увидим в следующем разделе).
Недостатки
- Алгоритм становится значительно медленнее по мере увеличения количества примеров и / или предикторов / независимых переменных.
Основной недостаток KNN в том, что он становится значительно медленнее по мере увеличения объема данных, что делает его непрактичным выбором в средах, где необходимо делать прогнозы быстро.Более того, существуют более быстрые алгоритмы, которые могут дать более точные результаты классификации и регрессии.
Однако при условии, что у вас достаточно вычислительных ресурсов для быстрой обработки данных, которые вы используете для прогнозирования, KNN может быть полезен при решении проблем, решения которых зависят от идентификации похожих объектов. Примером этого является использование алгоритма KNN в рекомендательных системах, приложение KNN-поиска.
Рекомендательные системы
В масштабе это выглядело бы как рекомендация продуктов на Amazon, статей на Medium, фильмов на Netflix или видео на YouTube.Хотя мы можем быть уверены, что все они используют более эффективные способы предоставления рекомендаций из-за огромного объема данных, которые они обрабатывают.
Однако мы могли бы воспроизвести одну из этих рекомендательных систем в меньшем масштабе, используя то, что мы узнали здесь, в этой статье. Построим ядро рекомендательной системы фильмов.
На какой вопрос мы пытаемся ответить?
Учитывая наш набор данных о фильмах, какие 5 фильмов наиболее похожи на запрос фильма?
Сбор данных о фильмах
Если бы мы работали в Netflix, Hulu или IMDb, мы могли бы получить данные из их хранилищ данных.Поскольку мы не работаем ни в одной из этих компаний, нам приходится получать наши данные другими способами. Мы могли бы использовать некоторые данные фильмов из репозитория машинного обучения UCI, набор данных IMDb или кропотливо создать свои собственные.
Изучите, очистите и подготовьте данные
Где бы мы ни получали наши данные, в них могут быть некоторые ошибки, которые нам необходимо исправить, чтобы подготовить их для алгоритма KNN. Например, данные могут быть не в том формате, который ожидает алгоритм, или могут отсутствовать значения, которые мы должны заполнить или удалить из данных, прежде чем передавать их в алгоритм.
Наша реализация KNN, описанная выше, основана на структурированных данных. Он должен быть в виде таблицы. Кроме того, реализация предполагает, что все столбцы содержат числовые данные и что последний столбец наших данных имеет метки, с которыми мы можем выполнять некоторые функции. Итак, откуда бы мы ни брали данные, нам нужно привести их в соответствие этим ограничениям.
Приведенные ниже данные являются примером того, на что могут быть похожи наши очищенные данные. Данные содержат тридцать фильмов, включая данные по каждому фильму семи жанров и их рейтинги IMDB.В столбце ярлыков все нули, потому что мы не используем этот набор данных для классификации или регрессии.
Набор данных рекомендаций по самодельным фильмамКроме того, существуют отношения между фильмами, которые не будут учитываться (например, актеры, режиссеры и темы) при использовании алгоритма KNN просто потому, что данные, которые фиксируют эти отношения, отсутствуют в данных устанавливать. Следовательно, когда мы запускаем алгоритм KNN на наших данных, сходство будет основываться исключительно на включенных жанрах и рейтингах фильмов на IMDB.
Используйте алгоритм
Представьте себе на мгновение. Мы просматриваем веб-сайт MoviesXb, вымышленное дочернее предприятие IMDb, и находим The Post . Мы не уверены, что хотим его смотреть, но нас заинтриговали его жанры; нам интересно узнать о других подобных фильмах. Мы прокручиваем вниз до раздела «Еще как это», чтобы увидеть, какие рекомендации сделает MoviesXb, и алгоритмические механизмы начинают вращаться.
Веб-сайт MoviesXb отправляет запрос на сервер для 5 фильмов, наиболее похожих на The Post .На сервере есть набор данных рекомендаций, точно такой же, как у нас. Он начинается с создания представления строки (более известного как вектор функций ) для The Post , затем запускается программа, аналогичная приведенной ниже, для поиска 5 фильмов, наиболее похожих на The Post , и наконец, отправляет результаты обратно на сайт MoviesXb.
Когда мы запускаем эту программу, мы видим, что MoviesXb рекомендует 12 Years A Slave , Hacksaw Ridge , Queen of Katwe , The Wind Rises и A Beautiful Mind .Теперь, когда мы полностью понимаем, как работает алгоритм KNN, мы можем точно объяснить, как алгоритм KNN дал эти рекомендации. Поздравляем!
Алгоритм k-ближайших соседей (KNN) — это простой алгоритм машинного обучения с учителем, который можно использовать для решения задач классификации и регрессии. Его легко реализовать и понять, но у него есть серьезный недостаток: он значительно замедляется по мере роста размера используемых данных.
KNN работает, находя расстояния между запросом и всеми примерами в данных, выбирая указанное число примеров (K), ближайших к запросу, затем голосует за наиболее частую метку (в случае классификации) или усредняет метки (в случае регресса).
В случае классификации и регрессии мы увидели, что выбор правильного K для наших данных осуществляется путем проверки нескольких K и выбора того, который работает лучше всего.
Наконец, мы рассмотрели пример того, как алгоритм KNN может быть использован в рекомендательных системах, приложение KNN-поиска.
.