Как решить задачу разными способами: ГДЗ по математике, 2 класс, Моро М.И. Реши задачи разными способами. – Рамблер/класс – Урок по математике «Решение задач разными способами»

Содержание

Урок по математике «Решение задач разными способами»

Тема “Решение задач разными способами”

Вид: закрепление умения решать задачи на основе расширения способа действия.

Цели:

научить решать задачи арифметическим и алгебраическим способом;
научить решать усложненные уравнения.

Ход урока

1. Орг. момент.

(Пальчиковая гимнастика)

Эмоционально-психологический настрой на урок. (Цель: создать эмоционально-психологический контроль)

Мне вспомнилась одна пословица “Корень ученья горек, да плод его сладок”. Как вы понимаете эту пословицу?

Она очень подходит к нашему уроку и вы это поймете.

2. Сообщение темы и цели урока.

— Тема нашего урока “Решение задач разными способами”

— Запишите число и тему урока.

3. Актуализация знаний.

— Мы с вами уже решали очень много самых разных задач, а сегодня я предлагаю вам решить необычные задачи, а задачи в которых есть буквенное значение.

(Дети записывают решение в тетради.)

В зале занято 6 рядов по в мест. Сколько мест занято?
А сколько свободных мест, если в зале а мест?
Длина прямоугольника 8 см. Найдите периметр квадрата.
— Можно решить эту задачу? (Эта задача требует пояснения при решении. Если прямоугольник является квадратом, то задача имеет решение, а если нет, то задачу решить нельзя)
Скоро Новый Год и я предлагаю вам задание составить задачу с такими данными.Масса подарка 800 граммов.

4. Решение задачи.

Для ремонта школы привезли в одинаковых банках 90 кг зеленой краски и 180 кг белой краски. Зеленой краски было 18 банок. Сколько купили банок с белой краской?

Работа над задачей идет по плану:

1 этап – восприятие задачи.
2 этап – поиск плана решения (прикидка ответа)
3 этап – выполнение плана.
4 этап – проверка (сравнить с прикидкой)

1 способ.

1) 90 : 18 = 5 (кг) – в 1 банке.

2) 180 : 5 = 36 (б)

2 способ.

1) 180 : 90 = 2 (раза) – во сколько раз за белую краску заплатили больше, чем за зеленую.

2) 18 х 2 = 36 (банок.)

— Ребята, что обозначает часть или целое число 90? 18? 180?

— Где мы еще с вами можем встретить часть и целое? (В уравнении)

5. Физминутка.

Если неизвестное число находится сложением – приседаете,

Вычитанием – руки вверх,

Умножением – хлопаем,

Делением – руки вперед.

А – 7 = 18 35 : а = 7 а + 6 = 10
30 – а = 13 а : 12 = 5 а х 4 = 24

— Назовите уравнения, где а – целое.

Решите уравнения второго столбика (по вариантам)

— Ребята, а что такое уравнение?

— А попробуйте теперь решить в паре такое уравнение:

а : 4 = 17 х 3

6. Расширение способа действия.

— Мы с вами решали задачу двумя способами. Это были арифметические способы решения. А давайте попробуем решить эту задачу еще одним способом – с помощью уравнения.

— Что мы возьмем за х?

— Вы уже говорили, что уравнение это равенство. Какая величина в нашей задаче равна, одинаковая?

— Исходя из этих данных составьте в группах уравнение по этой задаче. (180 : х = 90 : 18)

— Молодцы! Это алгебраический способ решения задачи.

7. РРО.

— Мы с вами уже решали задачи разными способами, а сейчас попробуйте записать решение задачи в виде уравнения.

Уровень 1.

Реши задачу, составив уравнение.

На крыше сидело 7 голубей. Когда к ним прилетело еще несколько, их стало 15. Сколько голубей прилетело?

Уровень 2.

Реши задачу, составив уравнение.

В 7 одинаковых коробках 21 кг винограда. Сколько килограммов винограда в 4 таких же коробках?

8. Итог урока.

— Разрешите закончить наш урок, задав вам несколько вопросов.

— С чем мы сегодня познакомились на уроке?

Чему вы научились?

9. Домашнее задание.

1 уровень. Найдите в учебнике задачи, которые можно решить уравнением.

2 уровень. Составьте 2 задачи, которые можно решить уравнением – простым и усложненным.

«Решение задач разными способами»

План урока математики в 4 классе

Учитель Одегова Л.В.

Тема: «Решение задач разными способами»

Цели: формировать умение решать задачи разными способами (арифметич, алгебраичес), формировать умение решать сложные уравнения, формировать вычислительные навыки;

развивать познавательную активность, содействовать развитию навыков сотрудничества, самоконтроля;

воспитывать любовь к природе, уважение к историческому наследию родного города и страны.

Методическая цель: достижение эффективности обучения через интенсивную коллективную и индивидуальную деятельность обучающихся.

Формы работы: индивидуальная, фронтальная, коллективная, групповая, в паре, самостоятельная.

Методы: ИКТ, словесный, проблемный

Приёмы: анализ, сравнение, синтез.

Оборудование: индивидуальные карточки, индивидуальные тетради (Тренажёры) компьютер, проектор, экран, презентация урока.

Предметные результаты: уметь решать задачи разными способами, находить среди них рациональные; преобразовывать задачи; решать сложные уравнения разными способами.

Личностные УУД: развитие учебно-познавательного интереса к новому материалу и способам решения задачи. Формирование уважительного и доброжелательного отношения к одноклассникам, самоопределение (внутренняя позиция, самоуважение, самооценка).

Познавательные УУД: формирование умения выдвигать гипотезы (предположения – что получится в результате) и проверять их. Рассуждать, анализировать, делать выводы. Строить речевое высказывание в устной и письменной форме.

Регулятивные УУД: в учебном сотрудничестве. Контролировать: обнаруживать и устранять ошибки. умение решать проблемы, управлять своей деятельностью, проявлять инициативу и самостоятельность.

Коммуникативные УУД: участвовать в коллективном обсуждении проблем; умение устанавливать и сравнивать разные точки зрения, выражать в речи свои мысли и действия

Ход урока Слайд 1

1.Орг. момент

Математику, друзья,
Не любить никак нельзя.
Очень строгая наука,
Очень точная наука,
Интересная наука —
Ма-те-ма-ти-ка!

-Нашим гостям интересно узнать, как мы умеем трудиться. А чтобы всё получилось, нужно быть предельно внимательными. Каким хотите видеть урок?

Слайд 2. Мудрые мысли «Опыт преодоления дает личности возможность полноценно развиваться, помогает становлению тех качеств, которые нужны для того, чтобы быть успешным в жизни».

Л. В. Занков

— Мы продолжаем набираться опыта в преодолении трудностей, чтобы быть успешными в жизни, чувствовать себя уверенно в разных ситуациях.

Мотив –Как связаны данные слова? делимое, частное, уравнение, множитель, делитель (карточки на наб. пол.)

2. Актуализация знаний 1) –Что такое уравнение? Что значит решить уравнение? Что такое корень уравнения? Как можно решить уравнение?

Слайд 3 – Найдите уравнение, которое не имеет корней.

а : 5 = 1400 – 900

2с + 7 = 2с – 7 6 (е + 4) = 132 ∙ 2

Класс решает уравнения (по выбору):

а : 5 = 1400 – 900 (2500) 6 (е + 4) = 132 ∙ 2 (40)

Проверка: -как решали? Слайд 4 Проверка

3. Работа над задачами.

— Прочитайте задачи. Слайд 5

— Из двух городов, расстояние между которыми 861 км, одновременно выехали навстречу две машины и встретились через 7 часов. Скорость одной машины 59 км/ ч. Определите скорость второй машины.

— Из двух городов, расстояние между которыми 861 км, одновременно выехали навстречу две машины и встретились через 7 часов. Скорость второй машины на 5 км больше скорости второй машины. Определите скорость второй машины.

— Что можете сказать об этих задачах.

— Чем похожи?

(Задачи на движение. В обеих задачах известно расстояние между городами, время движения до встречи. Одинаковые вопросы.)

— Чем отличаются? ( В первой задаче известна скорость первой машины, а во второй задаче, скорость обеих машин неизвестна.)

— Какие понятия встречаются в задачах на движение?

— Что такое скорость, время, расстояние?

— как найти скорость, время, расстояние? Слайд 6

4.Самостоятельная работа в парах с самопроверкой по плану:

Слайд 7

Запишите формулу, которая вам понадобится, чтобы ответить на вопрос задачи.
Составьте план решения задачи.
Решите задачу.
Сделайте проверку.

— Проверьте, так ли вы решили задачу.

— Как по-другому можно было решить задачу?

— Какой способ более рациональный?

— Почему?

— Прочитайте еще раз вторую задачу.

— Каким способом можно решить данную задачу?

(Алгебраическим способом).

5.Решение задачи алгебраическим способом.

— В уравнении должно быть неизвестное число, что возьмете за х?

(Коллективное составление уравнения). Слайд 8

— Пусть х – скорость первой машины, тогда х+5 – скорость второй машины.

( х + х+5) ∙ 7 = 861

(2х +5) ∙ 7 = 861

2х + 5= 861 : 7

2х + 5 = 123

2х= 123-5

2х = 118

х= 118:2

х= 59 (км/ч) скорость первой машины

59 + 5 = 64 (км/ч) скорость второй машины

— Можно ли эту задачу решить арифметическим способом?

861:7= 123 (км/ч) скорость сближения
123 – 5 = 118 (км/ч) одинаковая скорость обеих машин
118:2 = 59 (км/ч) скорость первой машины
59+5 = 64 (км/ч) скорость второй машины.

Слайд 9 Проверка: (59+64)∙ 7= 861

123∙ 7= 861

861= 861

— Сколькими способами решили вторую задачу?

— Попробуйте ответить на вопрос: Что значит, решить задачу разными способами?

— В конце урока вы скажете, зачем нужно уметь решать задачи разными способами.

Физкультминутка для глаз про весну Слайд 10

6.Усвоение новых знаний и способов действий

– 9 мая мы праздновали 72 годовщину Великой Победы над фашизмом. К празднику проводились различные фестивали, конкурсы, акции мира и добра. Вот одна из них.

Слайд 11 Решить задачу

— В нашем городе старшеклассники посадили в сквере липы и каштаны – всего 540 растений. При этом лип было в 5 раз больше, чем каштанов. Сколько посадили растений каждого вида?

Разбор задачи, решаем алгебраически

Работа в группах – составление уравнения

Проверка — у доски по 1 представителю от группы, объясняют

Вступительная часть

«Пусть х дер. – каштаны, тогда лип – 5х. Зная, что …. 5х + х =540 Слайд 12

х=90 –каштаны 2) 90∙5=450 –липы ( решение на доске 1 уч)

Проверка –устно. Арифметич способ – устно

— Какой способ понравился?

– Весной возвращаются в родные края перелётные птицы. Мы заочно порадуем гостей, расселим их в домики.

Слайд 13 Решить задачу

— Мы решили порадовать скворцов и смастерили для них новые домики. Одна группа расходовала 200 см доски, вторая – на 40 см меньше, чем первая, а третья – ½ того, что расходовали первая и вторая группы вместе. Хватит ли для работы шестиметровой доски? (решают в паре)

Слайд 14 Проверка, разные способы решения задачи, Выбирают рациональный.

Птицы будут благодарны вам.

Слайд 15 -Сформулируйте тему урока.

-Зачем нужно уметь решать задачи разными способами?

Слайд 16 Рефлексия: кто испытывал трудности и преодолел их?

Закончите фразу:

Сегодня на уроке я –

Разобрался, что значит решить задачу двумя способами.
Понял, что одну и ту же задачу можно решить по-разному.
Научился решать задачу разными способами.

Слайд 17 Оцените свою деятельность на уроке, используя смайлики.

Я умею решать задачи арифметическим и алгебраическим способом.

Я умею решать задачи только арифметическим способом.

Я испытываю трудности при решении задачи _____________ способом.

Дом задан. Слайд 18. Решить задачу в тренажёре разными способами.

Методическая разработка по математике (1 класс) по теме: Решение задач разными способами – средство повышения интереса к математике.

Войнова Светлана Юрьевна, учитель начальных классов,

МОУ «СОШ №56 с углубленным изучением отдельных предметов»

г. Саратов

Решение задач разными способами – средство повышения интереса к математике.

Люди научились считать 25-30 тысяч лет тому назад. О значении математики как предмета школьного преподавания М.В.Ломоносов в записке о преподавании физики, химии и математики пишет так:

«А математику уже затем учить следует, что она ум в порядок приводит».

Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.

Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.

Большие возможности для развития интереса учащихся к математике имеют задачи и их решения разными способами. Для кого из ребят интересна математика? Да математику любят в основном те ученики, которые умеют решать задачи, научив их решать задачи разными способами, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.

Однако в практике обучения математике различные способы решения ещё не заняли достойного места. Причин этому много, и в частности, недостаточная ориентация на эту работу в учебниках, методических пособиях для учителей. Учитель поэтому зачастую не владеет теми приёмами, с помощью которых можно отыскать другие способы решения. А без этого невозможно и детей научить находить разные способы решения, трудно использовать эти способы решения для других целей обучения и воспитания.

В начальном курсе математики текстовые задачи могут быть решены различными способами : алгебраическим, практическим, графическим, табличным, схематическим, комбинированным.

Рассмотрим различные способы решения текстовых задач на конкретных примерах.

Арифметический способ.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.

Задача. «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок, 6 лодок вернулись. Сколько лодок с рыбаками должно вернуться?»

I способ. 1. 20+8=28(л.) ушли в море.

2. 28-6=14(л.) должны вернуться.

Выражение.(20+8)-6=14(л.)

II способ. 1. Сколько больших лодок должно вернуться? 20-6=14(л.)

2. Сколько всего лодок должно вернуться? 14+8=22(л.)

Выражение.(20-6)+8=14(л.)

III способ. 1. Сколько маленьких лодок должно вернуться? 8-6=2(л.)

2.Сколько всего лодок должно вернуться? 20+2=22(л.)

Выражение.(8-6)+20=14(л.)

Ответ: должно ещё вернуться 22 лодки. Задача решена различными арифметическими способами.

Если у учащихся нет навыков решения задач различными арифметическими способами или вызывает затруднение их нахождение, можно предложить следующие методические приёмы:

1. разъяснение плана решения задачи;

2. пояснение готовых способов решения;

3. соотнесение пояснения с решением;

4. продолжение начатых вариантов решения;

5. нахождение «ложного» варианта решения из числа предложенных.

Алгебраический способ.

Текстовые задачи решаются либо синтетическим методом (вычисления в прямом порядке, от числовых данных условия к числовым результатам, о которых спрашивается в задаче), либо аналитическим (вычисления в обратном порядке с рассуждениями, идущими от вопроса задачи). Примерами этих последних являются задачи о «задуманном числе», а также задачи на части. Естественным оформлением решения таких задач служит составление уравнения – алгебраический метод. Он состоит из следующих шагов: 1.Введение неизвестного. 2.Выражение через это неизвестное величин, о которых говорится в задаче. 3.Составление уравнения. 4.Решение уравнения. 5.Осмысление результата и формулирование ответа.

Задача: «У Иры втрое больше наклеек, чем у Кати, а у Кати на 20 наклеек меньше, чем у Иры. Сколько наклеек у Кати?».

Вначале составим схему уравнения, содержащую не только математические знаки, но и естественные слова.

( Ирины наклейки) – (Катины наклейки) = 20 наклеек.

Получилась вспомогательная модель задачи – частичный перевод текста на математический язык. Введём неизвестное. Пусть х – число Катиных наклеек. Тогда число наклеек у Иры равно х 3.

Составим уравнение х * 3 – х = 20

2 * х = 20

Х=20:2

Х=10

Ответ: у Кати 10 наклеек.

При обучении алгебраическому методу решения текстовых задач полезно дополнить схему решения самым первым шагом – составлением схемы уравнения, в которую включаются как математические символы, так и нематематические записи и даже рисунки.

Графический способ.

Это способ решения задачи с помощью чертежа.

Задача: «Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?»

лещи окуни щуки

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

Построение чертежа помогает найти другой арифметический способ решения задачи.

Задача: «На одной машине увезли 28 мешков зерна, на другой на 6 мешков больше, чем на первой, а на третьей на 4 мешка меньше, чем на второй. Сколько мешков зерна увезли на третьей машине?»

I способ. 1. 28+6=34 (мешка) – увезли на второй машине.

2. 34-4=30 (мешка)- увезли на третьей машине.

Ответ : на третьей машине увезли 30 мешков зерна.

Если же мы построим чертеж к этой задачи, то легко найдем другой арифметический способ решения.

28 мешков

6 мешков

28 мешков

II.

4 мешка

28 мешков

III.

На сколько больше мешков увезли на третьей машине, чем на первой? 6-4=2(мешка)
Сколько мешков увезли на третьей машине? 28+2=30 (мешков)

Ответ: на третьей машине увезли 30 мешков зерна.

Из приведенных примеров следует вывод: графическое оформление задачи может определить ход мыслительного процесса и является средством выявления различных способов решения одних и тех же задач. При этом легче усматриваются разные логические основы, содержащиеся в условии задачи; такие способы определяются анализом наглядного сопровождения задачи, на которые учащиеся направляются постановкой учителем соответствующих заданий.

Логический способ.

Задача: «В 6 банок поровну разложили 12 кг варенья. Сколько надо таких же банок, чтобы разложить 24 кг варенья?»

В данном случае логическая основа задачи проявляется на двух уровнях – открытом и скрытом, т. е. здесь две логические основы. В первом случае направление мыслительного процесса определяется вопросами:

Сколько кг варенья помещается в одну банку? 12:6=2(кг)
Сколько банок потребуется для 24 кг варенья? 24:2=12(б.)

Во втором случае ход того же процесса определяется другими вопросами:

1.Во сколько раз больше стало варенья? 24:12=2(раза)

Если варенья стало в два раза больше, значит, и банок потребуется в два раза больше.

2.Сколько потребуется банок? 6 * 2=12(б.)

Ответ: потребуется 12 банок.

Табличный способ.

При решении некоторых задач хорошим подспорьем является табличная форма.

Задача: «У Саши в коллекции 8 жуков и пауков. У всех насекомых 54 ноги. У одного жука 6 ног, а у одного паука – 8ног. Сколько жуков и сколько пауков у Саши в коллекции?»

Количество жуков	Количество пауков	Количество ног у всех жуков	Количество ног у всех пауков	Всего ног
1	7	6	56	62
2	6	12	48	60
3	5	18	40	58
4	4	24	32	56
5	3	30	24	54

Ответ: у Саши в коллекции 5 жуков и 3 паука.

Схематический способ.

В числе способов решения задач можно назвать схематическое моделирование. В отличие от графического способа решения, который позволяет ответить на вопрос задачи, используя счёт и присчитывание, схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно представлять в виде символической модели (выражение, равенство). Тем не менее, моделирование текста задачи в виде схемы позволяет ответить на вопрос задачи. Покажу это на примере.

Задача: «В двух вагонах ехали пассажиры, по 36 человек в каждом вагоне. На станции из первого вагона вышло несколько человек, а из второго вагона вышло столько человек, сколько осталось в первом. Сколько всего пассажиров осталось в двух вагонах?»

В данном случае схема выступает как способ и как форма записи решения задачи.

Ответ: в двух вагонах осталось 36 человек.

Комбинированный способ.

В этом случае для записи решения задачи могут быть использованы одновременно схема и числовые равенства.

Задача: «В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось нераскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?»

Решение задачи можно оформить так:

Раскрасил

Осталось

48:3=16(л.)

Ответ: остались нераскрашенными 16 листов.

На всех уроках, если встречается задача, допускающая разные способы решения, стараюсь детям дать возможность найти их.

Я считаю, что очень важно и полезно после решения задачи разными способами предложить ребятам ряд заданий творческого характера. Рассмотрим некоторые из них на примере.

Задача: «С одной яблони собрали 15 кг яблок, а с другой 30 кг. Все эти яблоки разложили в ящики, по 5 кг в каждый. Сколько ящиков потребовалось?»

1 способ. (15+30):5=9(ящ.)

2 способ. 15:5+30:5=9(ящ.)

Главный вопрос после решения задачи: «Почему мы смогли решить задачу двумя арифметическими способами?» Потому что и 15, и 30 можно разделить на 5 без остатка.

Задания творческого характера.

1.Какие числовые данные можно использовать вместо 15 и 30, чтобы задача решалась двумя способами и почему? 10 и 45, 25 и 50…главное, чтобы оба числа делились на 5.

2.Какие числовые данные можно использовать вместо 5, чтобы задача решалась двумя способами и почему? 3, так как и 15, и 30 можно разделить на 3 без остатка.

3.Яблоки разложили в ящики по 4 кг. Какие числовые данные можно взять вместо 15 и 30, чтобы задача решалась двумя способами и почему? 8 и 32, 16 и 40…главное, чтобы оба числа делились на 4 без остатка.

4.С яблонь собрали 21 кг и 27 кг яблок. По сколько кг яблок можно разложить в один ящик, чтобы задача решалась двумя способами и почему? По 3 кг, так как и 21, и 27 можно разделить на 3 без остатка.

5.Составьте аналогичную задачу по выражению, чтобы она решалась двумя способами. (12 +…) : 6

Умелое использование различных способов решения задач на уроках математики в начальных классах оказывает положительное влияние на развитие мышления и творческих способностей детей, на формирование их личности и исследовательских навыков, является залогом устойчивого интереса к математике.

Решение задач разными способами. 2-й класс

Задачи урока: закреплять умение решать задачи изученных видов разными способами; совершенствовать вычислительные навыки и навыки устного счёта; развивать внимание и логическое мышление.

Планируемые результаты

Предметные. Выполнять устные и письменные вычисления изученных видов в пределах 100. С помощью рисунка, схематического чертежа и краткой записи решать задачи. Распознавать и изображать геометрические фигуры. Использовать в речи название компонентов математических действий.

УУД (универсальные учебные действия)

Коммуникативные. Участвовать в диалоге, слушать и понимать других, высказывать свою точку зрения на события, поступки. Выполнят различные роли в паре, сотрудничать в совместном решении проблемы, управлять поведением партнёра.
Познавательные. Осознанное построение речевого высказывания в устной форме. Выделение и формирование учебной цели. Смысловое чтение; извлечение необходимой информации из текста. Самостоятельное создание алгоритмов деятельности при решении проблем. Обобщение, рассуждение и обоснование выводов.
Регулятивные. Самостоятельная организация своего рабочего места. Следовать режиму организации учебной деятельности. Определять цели учебной деятельности с помощью учителя. Составлять план и последовательность действий. Соотносить выполненное задание с образцом, предложенным учителем. Вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта сделанных ошибок. Стабилизация эмоционального состояния для решения различных задач.
Личностные. Выполнять задания поискового характера. Понимать учебную задачу и стараться её выполнить. Работа в парах. Отвечать на итоговые вопросы, подводить итог урока. Контролировать свою работу и её результат.

Оборудование: интерактивная доска, мультимедийный проектор, ноутбук учителя, ноутбуки учеников.

ХОД УРОКА

1. Организационный момент

– Создадим хорошее настроение себе и нашим гостям. Улыбнитесь друг другу и гостям, садитесь!

– Откройте тетради. Посмотрите свои достижения. Запишите число, классная работа.

Ну-ка, посмотри, дружок,
Ты готов начать урок?
Все ли на месте?
Всё ли в порядке?
Книжки, ручки, тетрадки, ноутбуки?
Все ли правильно сидят?
Все ли внимательно глядят?

2. Актуализация знаний

а) Логическая разминка.
Кто догадался, что надо сделать?
– Нарисуйте человечка в тетради.
Проверка. Вставить карточку с человечком в таблицу.
– У кого настроение улучшилось?

б) – Проиграем в круговые примеры.
– Какие примеры называются «круговыми»?
– Проверим, будут ли эти примеры «круговые».

34 – 20                     6 + 28
              74 – 70
12 : 2                       14 + 30
44 + 30                    4 * 3

– Почему эти примеры «круговые»?

3. Решение задач на нахождение третьего слагаемого.

а) – Что видите на рисунке? (Арбуз, тыкву, дыню)
– Сколько весит тыква? Дыня? Арбуз?
– Что обозначает число 12?
– Рассмотрите выражения на карточках.

3 + 5 12 – (3 + 5) 12 – 3 12 – 3 – 5

– Запишите в тетради выражение, с помощью которого можно узнать, сколько весят дыня и тыква.

3 + 5 = 8 (кг)

– Запишите в тетради выражение, с помощью которого можно узнать, сколько весят арбуз и тыква.

12 – 3 = 9(кг)

– Запишите в тетради выражение, с помощью которого можно узнать, сколько весит арбуз.

12 – 3 – 5 = 4 (кг) 12 – (3 + 5) = 4(кг)

– Что можно сказать о двух последних выражениях? (Разные способы решения одной задачи)
– Кто может сформулировать тему урока? (Решение задач разными способами)

б) Решение задачи в тетради.

Один ученик решает задачу на доске.

– Прочитайте задачу.
– Как надо решить задачу. (Разными способами)
– Составим схематический чертёж к задаче.
Решим задачу, записав выражение.
25 – (5 + 8) = 12(с.) – прочитала вечером
Ответ: 12 страниц.
– Кто решил задачу другим способам?
25 – 5 – 8 = 12(с.) – прочитала вечером

в) Работа в парах.

– Как надо работать в парах?
– Включите ноутбуки (диск «Математика», 2 часть, с.76, 2 задание).
– Что надо сделать?

Проверка на интерактивной доске.

– Какого вида решали задачи? (Нахождение третьего слагаемого)

Физминутка для глаз.

Закрыть глазки, открыть.
Нарисовать глазками круг, треугольник.

4. Геометрическая задача

а) Какая фигура на доске? (Прямоугольник)

– Что такое прямоугольник?

б) Прочитайте задание на с.77

Выполнить задание самостоятельно.

в) Проверка.

Работа в парах. Посмотрите, как начертил прямоугольник сосед.

Проверить решение задачи разными способами. Записать каждый способ на доске.

(1 + 10) * 2 = 22 (см) – периметр прямоугольника
(1 * 2) + (10 * 2) = 22 (см) – периметр прямоугольника
1 + 1 + 10 + 10 = 22(см) – периметр прямоугольника

– Какого вида задачу повторили? (Нахождение периметра)

5. Рефлексия учебной деятельности

а) – Что повторили сегодня на уроке?
– Что больше всего запомнилось?

б) Какими словами вам хочется закончить урок?

Сегодня я узнал…
Было интересно…
Я понял, что…
Теперь я могу…
Я почувствовал…

Урок математики «Решение задач разными способами»

Урок математики

3 класс

Учитель начальных классов

I категории высшего

уровня квалификации

Очкурова Светлана Викторовна

Тема урока: Решение задач разными способами.

Цель: формирование умения решать задачи разными способами.

Задачи:

Совершенствовать умения умножать и делить числа, умения в решении задач разными способами и выборе рационального способа;
Развивать умения самостоятельно оценивать результат своих действий, контролировать себя, находить и исправлять собственные ошибки, развивать внимание, память познавательную активность учащихся.
Воспитывать у учащихся умение вести учебный диалог; совершенствовать коммуникативные навыки, аккуратность при работе в тетради.

Ход урока

Организационный момент

Деление класса на группы, жребий. Распределение ролей:

Писарь – записывает решение;

Спикер – защита решения, ответ от имени группы;

Организатор – распределяет роли, следит за временем, действиями всех членов группы.

Планировщик – исследует условия поставленной задачи и планирует работу;

Исполнитель – осуществляет попытки решения;

Критик-контролер – проверяет соответствие и оценивает, подвергает сомнению мнение группы.

Повторение правил работы в группе.

Целеполагание

—Для того, чтобы определить тему урока, необходимо выполнить задание. Перед вами лабиринт. Что это такое? (головоломка, состоящая из запутанных путей) В лабиринте перед вами стоит задача: нужно помочь ученику пройти из школы домой. Рассмотрите каждый лабиринт, работая в группе, проанализируйте, какими способами ученику можно попасть домой? Соотнеся задание с уроком, сформулируйте тему урока. (учащиеся называют тему урока: “ Решение задач разными способами” )

-Мы работали по данной теме на прошлых уроках? Сегодня урок закрепления по теме: «Решение задач разными способами»

-Попытайтесь определить учебные задачи, которые мы должны достичь к концу урока. Вам помогут слова помощники «закрепить…», «обобщить…»

-Урок посвятим решению задач. Решая задачи, о многом можно узнать. Задачи учат нас рассуждать, анализировать, наблюдать, вычислять.

Актуализация имеющихся знаний

-Но прежде чем преступить к работе по теме урока мы проведём устный счет

Устный счёт

Игра “Верно — неверно”.

(Если высказывание верно, учащиеся записывают в тетради — да, если ложно – нет.)

— Произведение чисел 6 и 8 равно 56.

— Сумма чисел 20 и 3 равна 23.
— Разность чисел 40 и 8 равна 38.

— 56 разделить на 7 получится 8.
— Если 4 умножить на 6, получится 24.
— Если из 33 вычесть 8, получится 26.
— Число 75 больше 70 на 5.

— Частное чисел 42 и 6 равно 8.

Проверка по эталону с доски. Выставление оценок. Работа выполнена без ошибок – «5», 1 ошибка – «4», 2 ошибки – «3»,3 и более ошибок – «2».

— У кого «4» и «5»? Кто не справился с этим заданием? В чем причина допущенных ошибок? Какие знания и умения потребовались? (знание таблицы умножения, компонентов умножения и деления

Работа по теме урока

Решение задач разными способами.

Один из учеников 3 класса решал задачу разными способами. Справился ли он с заданием, мы узнаем, когда выполним проверку. Оценивать задание будем с помощью критериальной карты. По каким критериям будем оценивать задачу? Прочтите их. Внимательно прочтите дескрипторы. Какое максимальное количество баллов можете поставить за работу? Как должна быть выполнена работа на «5»?

— Какие умения понадобятся?

-Выполняем работу в паре.

В столовой на тарелки раскладывали булочки и пирожки. Получилось 10 тарелок с булочками по 5 на каждой и 10 тарелок с пирожками по 4 на каждой. Сколько всего булочек и пирожков разложили?

10т. по 5 б.

10т. по 4п.

1 способ:

1) 10*5=50 (б.) всего булочек

2)10*4=40 (п.) всего пирожков

3)50+40=90 (шт.)

(10*5)+(10*4)=90

2 способ:

1) 5+4=9 (шт.) пирожков и булочек в 1 тарелке

2)9*10=90 (шт.)

(5+4)*10=90

Ответ: всего разложили 90 булочек и пирожков.

Проверка полученных результатов. Оцените решение задачи по критериальной карте. Какую оценку поставим за решение задачи? Почему?

Физминутка

Закрепление

Практическая работа в группах.

С одной яблони собрали 15 кг яблок, а с другой 30 кг. Все эти яблоки разложили в ящики, по 5 кг в каждый. Сколько ящиков потребовалось?

1 — 15 кг по 5 кг

? ящ.

2 – 30 кг по 5 кг

I способ. 1) 15 + 30 = 45 (кг) собрали яблок с двух яблонь.

2) 45 : 5 = 9 (ящ.) потребовалось.

Выражение. (15 + 30) : 5 = 9 (ящ.)

II способ. 1)15 : 5 = 3 (ящ.) потребовалось для яблок с первой яблони.

2) 30 : 5 = 6 (ящ.) потребовалось для яблок со второй яблони.

3) 3 + 6 = 9 (ящ.) потребовалось всего.

Выражение. 15 : 5 + 30 : 5 = 9 (ящ.)

Ответ: потребовалось 9 ящиков.

— Запишите краткую запись и решите задачу разными способами, записывая решение по действиям и выражением.

Проверка по группам (меняются работами по часовой стрелке — стратегия «Карусель») с помощью критериальной карты.

— Какие группы справились с заданием на «4» и «5»? Вывешивают работы на доску. Какие ошибки допустили? В чем причина допущенных ошибок?

Домашнее задание

Предлагаю вам на выбор решить задачу разными способами.

Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок, 6 лодок вернулись. Сколько лодок с рыбаками должно вернуться?»
В микроавтобусе 11 мест для пассажиров. Сколько человек можно перевезти в трех таких автобусах, если каждый из них сделает 10 рейсов?

Итог урока. Рефлексия.

— Урок подходит к концу. Проанализируйте свою работу.

— Все ли удалось сделать? Какие трудности встретились? Довольны ли вы своей индивидуально работой на уроке? Работой в группе?

-Над чем следует работать в дальнейшем?

Рефлексию работы на уроке учащиеся осуществляют с помощью метода «Рефлексивная мишень»

— Оцените свою работу, наклеив знак в нужном секторе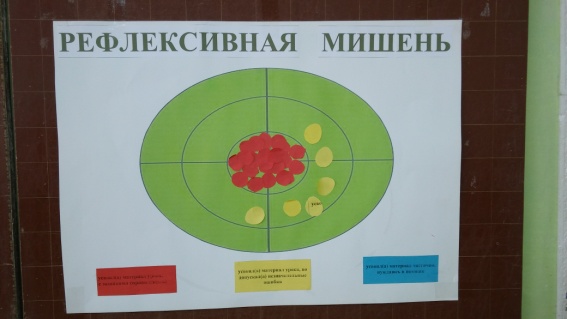

Красный – усвоил(а) материал урока, с заданиями справился(ась)

Желтый – усвоил(а) материал урока, но допускал(а) незначительные ошибки

Синий – усвоил(а) материал частично, нуждаюсь в помощи

Анализ результатов.

Решение составных задач разными способами

Цель: Закрепить умение решать задачи изученного вида разными способами

Задачи: Рассматривая и сравнивая разные виды задач и способы их решения, используя метод моделирования, совершенствовать мыслительные навыки; закреплять навыки счета в пределах 100.

Развивать гибкость мышления, математическую речь.

Продолжить работу над развитием профиля студента и всех видов навыков, организовав работу в группах по уровням и предоставив возможность презентовать работу.

Оборудование: задания на листах для каждой уровневой группы, кубики, клей, цветная бумага, фломастеры, линейки, формат А3.

Ход урока:

I.Орг. момент. Приветствие.

— Сегодня девизом нашего урока будет китайская мудрость:

«Я слышу — и забываю,

я вижу — и запоминаю,

я делаю – и понимаю».

— Почему говорится, что когда делаешь сам, то понимаешь?

II. Устный счёт

А) «мозговой штурм»

-Какое число было 3 дня назад?

-Какой день недели будет послезавтра?

У жука 3 пары ног. Сколько всего ног у жука?

— В семье двое детей. Саша брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?

Б) Впиши число вместо знака:

7 3 6 4 9 5 6 5 4

16 18 ?

В) — А сейчас проверим, как вы можете «на слух» решать задачи. Я читаю задачу, а вы в тетрадь записываете только ответ.

Задачи:

1. На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?

2. В корзине лежит 14 яблок и 6 груш. Сколько всего фруктов лежит в корзине?

3. У Ромы было 20 марок. Папа подарил ему ещё 7 марок. Сколько марок стало у Ромы?

4.В I коробке 8 ручек, во II – 10 ручек. А в III коробке столько ручек, сколько в I и во II коробках вместе. Сколько ручек в III коробке?

5. У Саши было 80 тенге. Он потратил 50 тенге. Сколько тенге осталось у Саши?

6. У Юли было 11 кукол, а зайчат на 6 меньше. Сколько зайчат было у Юли?

7. Альбом стоит 100 тенге, а блокнот 80 тенге. На сколько тенге альбом дороже блокнота?

Проверка: 16, 20, 27, 18, 30, 5, 20.

— Какие виды задач встретились?

(Учитель выставляет в глоссарий слова: задача, нахождение суммы, на увеличение, на уменьшение, нахождение остатка, на сравнение)

_ Сколько действий надо было выполнить, чтобы ответить на вопрос задачи? (Одно).

— Что можно сделать, чтобы задачи решались двумя действиями?

Ответ: 1.Изменить вопрос, чтобы действий стало больше.

2. Дополнить условие (добавить числа), не изменяя вопроса.

3.Изменить текст задачи.

III.Постановка проблемы.

— Сегодня мы будем решать задачи в 2 действия и постараемся доказать такую гипотезу:

Задачу можно решить разными способами.

IV. План урока:

1.Определение структуры задачи

2. Исследование способов решения задачи

3. Презентация

Актуализация знаний. Работа с глоссарием.

— Из каких частей состоит задача? ( В глоссарий выставляются слова: условие, вопрос, схема, модель, решение, ответ)

-Как можно доказать гипотезу? (Решить задачи разными способами).

Определение знаний по континууму и деление на группы

1 группа – начинающий уровень

2 группа – базовый уровень

3 группа – творческий уровень

V. Исследование способов решения

Каждая группа получает простую задачу, преобразовывает её в составную, решает разными способами, сопровождая моделью или схемой.

1 группа (работает под руководством учителя)

Задача: На одном проводе сидело 8 ласточек, а на другом на 4 ласточек больше. Сколько ласточек сидело на втором проводе?

— Измените вопрос задачи так, чтобы она решалась двумя действиями. Решите задачу разными способами.

Изменяют вопрос – Сколько всего ласточек сидело на проводе? В ходе исследования получается на листе продукт:

Условие:

1провод -8 ласт. ?

2 провод -?л., на4 больше

Схема:

Решение: 1 способ

1) 8+4=12 (л) — на 2 проводе

2) 8+12=20(л) – всего

2 способ

1) 8+8=16 (л) – если бы было поровну

2) 16+4=20(л) – всего

Ответ: 20 птиц всего

2 группа

Задача: У Саши было 80 тенге. Он потратил 50 тенге на ручку. Сколько тенге осталось у Саши?

( Дополните условие так, чтобы задача решалась двумя действиями. Решите задачу разными способами).

(Добавляют условие: он потратил 50 тенге на ручку и 20 тенге на ластик)

Условие:

Было – 80 тг

Потратил 50 тг и 20 тг

Осталось -?тг

Схема:

Решение:

1способ

1)50+20=70 (тг)-потратил

2)80 – 70 = 10(тг)- осталось

2 способ

1)80-50=30(тг)-осталось после покупки ручки

2) 30-20=10(тг) – осталось

3способ

1)80-20=60(тг)-осталось после покупки ластика

2) 60-50=10(тг) – осталось

Ответ: 10 тенге осталось у Саши.

3 группа

Задача: На фотоплёнке а кадров. В первый день Юра сделал в снимков, а во второй день на 4 больше. Сколько не отснятых кадров осталось на фотоплёнке?

— Определите, какие способы решения подходят к этой задаче: А, Б, В.

А) 1) + 2) + 3) –

Б) 1) + 2) — 3) –

В) 1) — 2) + 3) –

(Начертите чертёж к задаче, вставьте подходящие числа и решите её разными способами)

Чертеж: а

в в+4 ? тг

VI. Презентация. Каждая группа презентует задачу, называя из каких простых задач она состоит и способы решения.

VII. Какие концепции помогли нам доказать гипотезу?

(виды задач- функция,

способы решения – размышление, изменение)

VIII. Оценивание по континууму:

1)Гипотезу доказали.

Всё понятно.

Умею решать задачи разными способами.

2)Гипотезу доказали частично.

Затрудняюсь в понимании.

3) Мне было трудно. Нужна помощь.

Итог урока:

— Какое задание было трудным?

— А какое задание было наиболее интересным?

— Как оцените работу своей группы? Какими вы были на уроке?

Просмотр содержимого документа
«Решение составных задач разными способами»

Открытый урок

по математике во 2 классе

Тема: Решение составных задач разными способами

Составила Шемолина О. А.

Алматы

МКНО

2013 год

Цель: Закрепить умение решать задачи изученного вида разными способами

Развивать гибкость мышления, математическую речь.

Ход урока:

I.Орг. момент. Приветствие.

— Сегодня девизом нашего урока будет китайская мудрость:

«Я слышу — и забываю,

я вижу — и запоминаю,

я делаю – и понимаю».

— Почему говорится, что когда делаешь сам, то понимаешь?

II. Устный счёт

А) «мозговой штурм»

-Какое число было 3 дня назад?

-Какой день недели будет послезавтра?

У жука 3 пары ног. Сколько всего ног у жука?

— В семье двое детей. Саша брат Жени, но Женя Саше не брат. Может ли так быть? Кто Женя?

Б) Впиши число вместо знака

7 3 4 9 6 5

166

6 5 4

Задачи:

2. В корзине лежит 14 яблок и 6 груш. Сколько всего фруктов лежит в корзине?

3. У Ромы было 20 марок. Папа подарил ему ещё 7 марок. Сколько марок стало у Ромы?

5. У Саши было 80 тенге. Он потратил 50 тенге. Сколько тенге осталось у Саши?

6. У Юли было 11 кукол, а зайчат на 6 меньше. Сколько зайчат было у Юли?

7. Альбом стоит 100 тенге, а блокнот 80 тенге. На сколько тенге альбом дороже блокнота?

Проверка: 16, 20, 27, 18, 30, 5, 20.

— Какие виды задач встретились?

_ Сколько действий надо было выполнить, чтобы ответить на вопрос задачи? (Одно).

— Что можно сделать, чтобы задачи решались двумя действиями?

Ответ: 1.Изменить вопрос, чтобы действий стало больше.

2. Дополнить условие (добавить числа), не изменяя вопроса.

3.Изменить текст задачи.

III.Постановка проблемы.

— Сегодня мы будем решать задачи в 2 действия и постараемся доказать такую гипотезу:

Задачу можно решить разными способами.

IV. План урока:

1.Определение структуры задачи

2. Исследование способов решения задачи

3. Презентация

Актуализация знаний. Работа с глоссарием.

-Как можно доказать гипотезу? (Решить задачи разными способами).

Определение знаний по континууму и деление на группы

1 группа – начинающий уровень

2 группа – базовый уровень

3 группа – творческий уровень

V. Исследование способов решения

1 группа (работает под руководством учителя)

( Измените вопрос задачи так, чтобы она решалась двумя действиями. Решите задачу разными способами).

Условие:

1провод -8 ласт.

2 провод -?л., на4 больше

Схема:

Решение: 1 способ

1) 8+4=12 (л) — на 2 проводе

2) 8+12=20(л) – всего

2 способ

1) 8+8=16 (л) – если бы было поровну

2) 16+4=20(л) – всего

Ответ: 20 птиц всего

2 группа

Задача: У Саши было 80 тенге. Он потратил 50 тенге на ручку. Сколько тенге осталось у Саши?

( Дополните условие так, чтобы задача решалась двумя действиями. Решите задачу разными способами).

(Добавляют условие: он потратил 50 тенге на ручку и 20 тенге на ластик)

Условие:

Было – 80 тг

Потратил 50 тг и 20 тг

Осталось -?тг

Схема:

Решение:

1способ

1)50+20=70 (тг)-потратил

2)80 – 70 = 10(тг)- осталось

2 способ

1)80-50=30(тг)-осталось после покупки ручки

2) 30-20=10(тг) – осталось

3способ

1)80-20=60(тг)-осталось после покупки ластика

2) 60-50=10(тг) – осталось

Ответ: 10 тенге осталось у Саши.

3 группа

Задача: На фотоплёнке а кадров. В первый день Юра сделал в снимков, а во второй день на 4 больше. Сколько не отснятых кадров осталось на фотоплёнке?

— Определите, какие способы решения подходят к этой задаче: А, Б, В.

А) 1) + 2) + 3) –

Б) 1) + 2) — 3) –

В) 1) — 2) + 3) –

(Начертите чертёж к задаче, вставьте подходящие числа и решите её разными способами)

Чертеж: а

в в+4 ? тг

VII. Какие концепции помогли нам доказать гипотезу?

(виды задач- функция,

способы решения – размышление, изменение)

VIII. Оценивание по континууму

Гипотезу доказали.

Всё понятно. Умею решать задачи разными способами.

Гипотезу доказали частично.

Затрудняюсь в понимании .

Мне было трудно. Нужна помощь.

Итог урока:

— Какое задание было трудным?

— А какое задание было наиболее интересным?

— Как оцените работу своей группы? Какими вы были на уроке?

Разные способы решения текстовых задач

Аннотация: В результате организации учебной деятельности учащихся при решении текстовых задач посредством комплексных методических приемов можно повысить коэффициент усвоения, ищущих различные способы решения.

Ключевые слова: задача, способы решения задач, методические приемы.

При составлении и преобразовании задач у ученика развивается логическое мышление, воображение, фантазия, формируется познавательный интерес к математике, развивается его творческий потенциал. Проблема заключается в отсутствии стремления учащихся к поиску разных способов решения текстовых задач.

Мною был проведен обучающий эксперимент, цель которого показать действенность определенных методических приемов на определенных этапах ее решения младшими школьниками.
Обучающимся была представлена задача: «В две корзины собрали 37 помидоров. После того, как для засолки из этих корзин взяли поровну помидоров, в одной осталось 8, а в другой 5. Сколько помидоров было в каждой корзине?» Мы конкретнее остановимся на определенных этапах работы над задачей. Для решения другим способом используем зависимость величин и схему.

В какой корзине было больше помидоров? (В первой)

– На сколько? (На 3 помидора).

– Почему? (Так как взяли поровну, а осталось в 1–й корзине 8, а во второй 5. Это видно на схеме).

– Что можно узнать по этим данным? (Сколько помидоров было бы в двух корзинах, если количество помидоров было бы одинаковым).

– Что можно узнать следующими действиями? (Сколько помидоров было во 2-й корзине).

– Что можно узнать по этим данным? (Сколько помидоров было в 1-й корзине).

Для решения 3-им способом используем зависимость величин и схем:

– В какой корзине было больше помидоров? (В 1-й).

– На сколько? (На 3).

– А что мы можем узнать по этим данным? (Сколько было бы помидоров в 2-х корзинах, если осталось бы поровну).

– А что мы сможем узнать по этим данным? (Сколько помидоров было в каждой корзине).

Рассмотрим методические приемы работы над задачей после ее решения:

Постановка нового вопроса:

– На сколько количество помидоров в 1-й корзине больше количества помидоров во второй корзине? Ученики сразу предлагают найти разность записанных в ответе решенной задачи чисел: 20–17.

– Ребята, вы решили эту задачу 6-ю действиями, а можно было бы решить эту задачу с меньшим количеством действий?

Сравните две схемы, как получилось число 3?

– Сколько действий можно выполнить, чтобы узнать на сколько помидоров в первой корзине было больше, чем во второй (1).

– Вспомните это действие (8–5=3).

– Как вы догадались? (видно на схеме).

Цели, которые возможно ставить при решении этой задачи: совершенствовать умение решать составные задачи; совершенствовать умения учащихся проводить анализ содержания задачи и составлять ее модель; обучение умению ставить вопросы к условию задачи; обучение умению обосновывать правильность решения задачи; формирование умений проверять решения задачи; формирование умения преобразовывать задачу и решать ее различными способами; проверка умения решать простые задачи, входящих в составную.

Методические приемы, использованные для организации работы над задачей: моделирование задачи; составление обратной задачи; изменение данных задачи, приводящие к изменению способа решения; постановка нового вопроса к уже решенной задаче; решение задачи разными способами.

Наиболее типичные ошибки, которые допустили ученики, при решении этой задачи, их направление и предупреждение. Непрочное знание соотношения: было, взяли, осталось. Предупреждение: предварительный повтор на простых задачах. Ошибка при выполнении второго действия, дети могут неправильно вычесть 13 из 37, получив 14. нужно сделать проверку суммой.

Предупреждение: решение простых задач такого типа. Неправильное определение количества взятых помидоров из каждой корзины: (обычно деление заменяют умножением). Предупреждение данной ошибки – решение аналогичных задач.

К этой задаче наиболее эффективной моделью для самостоятельного поиска решения является схема и чертеж.

Ответ: в 1-й корзине было 20, а во 2-й корзине было 17 помидоров.

Для достижения этих целей я воспользовалась 3-мя методическими приемами: нахождение ошибок в предложенных к задаче схемах, выбор среди нескольких данных схем той, которая соответствует задаче, установление соответствия между содержанием задачи и схемой – ее моделью.

Таким образом, в результате организации учебной деятельности учащихся при решении текстовых задач посредством комплексных методических приемов можно повысить коэффициент усвоения, ищущих различные способы решения.