Знакомство с задачей и её составными частями. Видеоурок. Математика 1 Класс
На данном уроке вы познакомитесь с задачей и ее логическими частями.
Среди данных текстов найдите текст задачи (рис. 1).

Рис. 1. Варианты текстов
Чтобы выполнить это задание, необходимо знать, чем отличается текст задачи от других текстов (рис. 2).
Текст задачи включает в себя две части – то, что известно – условие, то, что необходимо найти – вопрос.
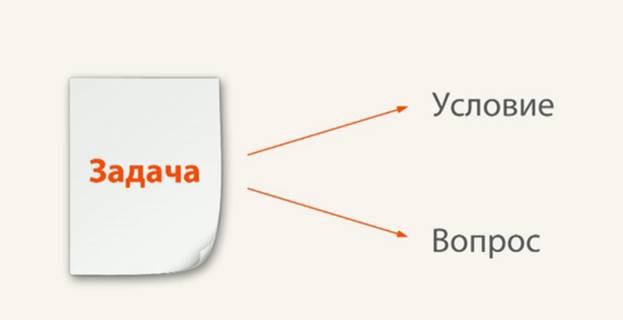
Рис. 2. Из чего состоит задача
Прочитайте первый текст.
Ваня поймал 4 рыбки, а Саша – 2 рыбки.
В этом тексте есть только условие, из которого мы узнали, сколько рыбок поймали мальчики. Вопроса в тексте нет, значит, это не задача (рис. 3).

Рис. 3. Текст без вопроса не является задачей
Прочитайте второй текст.
Ваня поймал 4 рыбки, а Саша – 2 рыбки. Сколько рыбок у Саши и Вани вместе?
В этом тексте нам известно, сколько рыбок поймал каждый мальчик, значит, есть условие. Еще в этом тексте записано, что надо найти, значит, есть вопрос. Значит, этот текст является задачей (рис. 4).

Рис. 4. Текст задачи
Прочитайте третий текст.
На сколько яблок больше, чем груш?
В тексте есть вопрос, но нет условия, следовательно, этот текст не является задачей (рис. 5).

Рис. 5. Текст без условия не является задачей
Второй текст – это задача, так как в нем есть 2 части: условие и вопрос.
Сделаем рисунок к задаче (рис. 6).
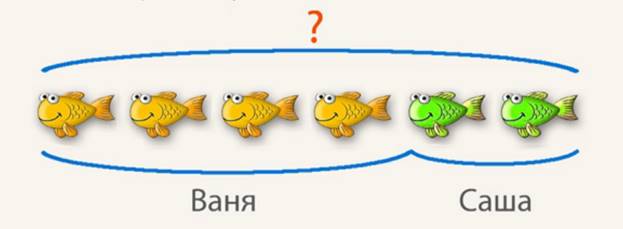
Рис. 6. Рисунок к задаче
Рисунок помогает установить, что неизвестно – целое или часть. Но если числа большие, то делать рисунки неудобно: слишком много предметов нужно рисовать. В этом случае на помощь приходит
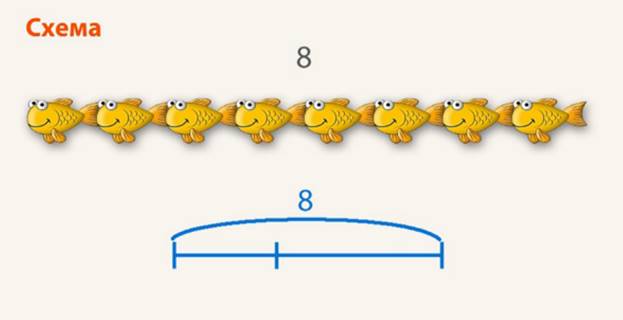
Рис. 7. Схема-отрезок
Схема – это часть задачи, которая поможет правильно установить взаимосвязь между условием и вопросом задачи.
Составим выражение к этой задаче и найдем его значение.
Чтобы составить выражение по рисунку или схеме, необходимо еще раз перечитать вопрос задачи.
Сколько рыбок у Вани и Саши вместе?
Мы знаем, сколько рыбок поймал Ваня и сколько рыбок поймал Саша, то есть нам известны части, а найти нам нужно целое (рис. 8).

Рис. 8. Что нужно найти
Чтобы найти целое, нужно части сложить: к 4 прибавим 2.
Мы составили выражение к данной задаче. Выражение – это еще одна часть задачи.
Найдем значение этого выражения. К 4 прибавим 2, получим 6.
В скобках запишем сокращенно слово «рыбки». Сокращаем до первой буквы гласного звука.
Полученное равенство называется решением задачи. Решение – это часть задачи.
Полученное значение выражения, 6 рыбок, является ответом. Ответ – это последняя часть задачи (рис. 9).

Рис. 9. Ответ задачи
Из каких логических частей состоит задача?
Когда мы читаем текст задачи, мы можем выявить только 2 части – условие и вопрос. Остальные части задачи – схема, выражение, решение и ответ – появляются в ходе решения задачи.
Соберите задачу. Соотнесите записи в рамках с соответствующими терминами (рис. 10).

Рис. 10. Задание на составление задачи
В первой рамке записано то, что нам известно, – это условие задачи.
Во второй рамке записано равенство – это решение задачи.
В третьей рамке записано, что надо узнать в задаче, – это вопрос задачи.
Наглядно показать условие и вопрос задачи нам помогает схема задачи в пятой рамке.
На схеме весь отрезок обозначает целое, то есть все конфеты, которые были у Даши сначала. 5 конфет на схеме поделили на две части: первая часть – это 2 конфеты, которые Даша отдала брату, вторая часть – это конфеты, которые остались у Даши. На схеме видно, что необходимо узнать, сколько конфет осталось у Даши. Значит, надо найти часть. Выбираем выражение, где из целого нужно найти часть. Соединяем шестую рамку с термином выражения.
Осталась одна рамка с ответом на вопрос задачи. Сколько конфет осталось у Даши? 3 конфеты – это ответ задачи (рис. 11).
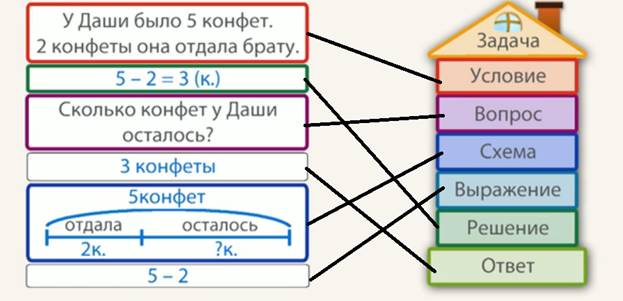
Рис. 11. Схема задачи
Иногда условие задачи прячется в вопросе задачи.
Сколько лап у двух котят?
Давайте попробуем узнать, что известно в этой задаче. По условию известно, что есть 2 котенка. А что еще нам известно, но об этом в задаче не говорят? Каждый из вас знает, что у котенка 4 лапки. Общие известные данные не всегда упоминаются в условии задачи.
Значит, нам известно, что есть 2 котенка и у каждого по 4 лапки – это условие задачи. Надо узнать, сколько лапок у двух котят – это вопрос задачи. Сделаем краткую запись содержания задачи с помощью схемы (рис. 12).
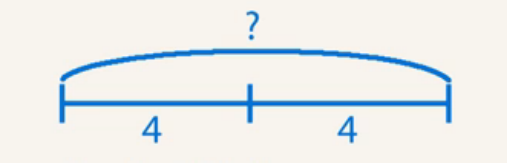
Рис. 12. Схема к задаче 2
На схеме видно, что надо найти целое. Составим выражение (рис. 13).
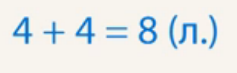
Рис. 13. Выражение для решения задачи 2
Значение выражения равно 8 – это ответ задачи. У двух котят 8 лапок (рис. 14).

Рис. 14. Иллюстрация задачи 2
Прочитайте текст задачи 3.
У Толи было 3 марки. Сестра подарила ему еще 2 марки.
Можно ли данный текст назвать задачей?
В этом тексте есть условие, но нет вопроса, значит, это не задача. Для того чтобы этот текст стал задачей, к условию надо выбрать вопрос.
1. Сколько марок было у Толи?
В первом вопросе хотят узнать то, что уже известно. Этот вопрос к данному условию задачи не подходит.
2. Сколько марок стало у Толи?
Второй вопрос задается о том, что нам неизвестно, и мы можем это узнать.
3. Сколько лет Толе?
Третий вопрос не соответствует условию задачи. Значит, этот вопрос лишний.
Оставляем второй вопрос, и у нас получилась задача.
У Толи было 3 марки. Сестра подарила ему еще 2 марки. Сколько марок стало у Толи?
Давайте решим ее, то есть ответим на вопрос задачи.
Составим выражение. Если сестра подарила Толе марки, то марок у Толи стало больше. Выбираем действие сложения (рис. 15).

Рис. 15. Действие сложения
Мы ответили на вопрос задачи, значит, мы ее решили.
Сегодня на уроке мы познакомились с задачами и ее логическими частями.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика. 1 класс. – М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика. 1 класс. – М: Астрель, 2012.
- Беденко М.В. Математика. 1 класс. – М.: Русское слово, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Социальная сеть работников образования Nsportal.ru (Источник).
- Ped-kopilka.ru (Источник).
- 7licei.3dn.ru (Источник).
Домашнее задание
- Из каких частей состоит задача?
- Задача.
На солнышке грелось 4 утенка. К ним прибежало 5 гусят. Сколько стало птиц?
А) Прочитайте условие задачи.
Б) Прочитайте вопрос задачи.
В) Нарисуйте схему задачи.
Г) Как решить данную задачу?
Д) Какой ответ получили?
- Решите задачу.
У Ванечки было 5 книг. Бабушка подарила ему еще 2 книги. Сколько книг стало у Ванечки?
- *Составьте задачу по рисунку и решите ее.

Рис. 16. Рисунок к задаче (Источник)

Рис. 17. Рисунок к задаче (Источник)
Обучающие карточки на тему «Оформление задач в начальной школе»
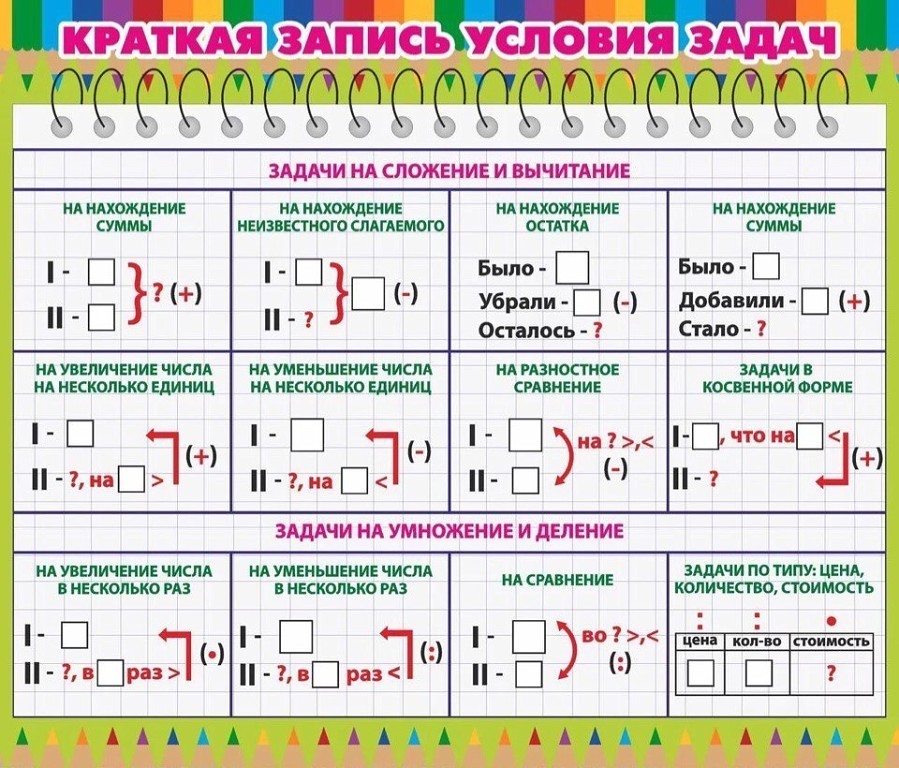
Основные виды краткой записи в начальной школе
Аннотация: Ученикам часто тяжело представить наглядно задачу. Облегчить процесс решения поможет краткая запись условия задачи. В краткой записи фиксируются величины, числа – данные и искомые, а также некоторые слова, показывающие, о чём говорится в задаче: «было», «положили», «стало» и т. п. и знаки, означающие отношения: «больше», «меньше», «одинаково» и т. п.
Краткую запись задачи ученик выполнять в виде: опорной схемы, таблицы, чертежа, с помощью геометрических фигур.
Для того чтобы краткая запись в максимальной степени способствовала решению задачи, нужно:
1)Краткую запись составлять на основе анализа текста задачи;
2)В краткой записи должно быть минимальное количество условных обозначений;
3)Количество вопросительных знаков в краткой записи должно соответствовать количеству действий в задаче;
4)Форму краткой записи выбирать такую, чтобы она более наглядно представляла условие задачи.
Варианты краткой записи
Задача: В двух бочонках у медведя было 17 кг меда. Из первого бочонка он съел 5 кг и в обоих стало поровну. Сколько кг мёда было в первом бочонке у медведя?
Нагляднее представит задачу запись в виде схемы
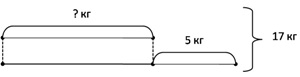
Над составной задачей форма работы предусматривает проверку умения учащихся по данным действиям решения задачи пояснить, на какой вопрос и с какой целью отвечает действие. В конце каждого действия пишем пояснение, доказательство того, что мы нашли этим действием. Эта форма помогает учащимся увидеть другие отношения, вести необходимую цепочку логических рассуждений, анализировать и делать выводы.
Ответ задачиЕсли использовались пояснения, ответ можно записать кратко. Если же не использовались, пишем полный ответ.
Задача на нахождение остатка
Задача: В детский сад привезли два бидона с молоком, по 20 л в каждом. За завтраком дети выпили 12 л молока. Сколько литров молока осталось?
Было — 20 л и 20 л
Выпили — 12 л
Осталось — ? л
Простая задача на деление на равные части, оформляем такие задачи в виде таблицы:
В I коробке Количество коробок Всего камней
? к. 3 к. 18 к.
Задача. Когда Маша полила 6 грядок, а Ира — 2 грядки, им осталось полить 3 грядки. Сколько всего грядок должны полить дети?
Было — ? гр.
Полили — 6 гр. и 2 гр.
Осталось — 3 гр.
Задача: Серёжа высадил 9 луковиц, по 3 луковицы в ряд. Сколько получилось рядов?
Это простая задача на деление по содержанию. Такую задачу нагляднее оформить картинкой.
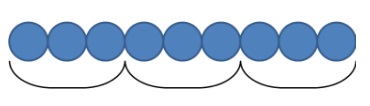
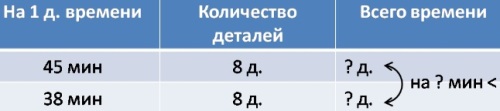
Составная задача на разностное сравнение, лучше оформить в виде таблицы.
Задача: Одну деталь мастер должен делать за 45 мин, а делает за 38 мин. Сколько времени сэкономит мастер, когда он сделает 8 деталей?
В помощь родителям!
Можно купить памятку в магазине книг!
математика: ЗАДАЧИ
СПОСОБЫ РЕШЕНИЙ ВСЕХ ВИДОВ ЗАДАЧ Задание
Прочитай задачу и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Объяснение
Например, в задаче:
В вазе 3 белых и 2 розовых гвоздики. Сколько всего гвоздик в вазе?
————————————————- —————————————
Опорные слова – это основа краткой записи.
В указанной задаче опорные слова:
Первое опорное слово – БЕЛЫХ (выделено жирным), который сокращаем в первом классе Б., но, начиная со второго класса, БЕЛ.
Второе опорное слово – РОЗОВЫХ (выделено жирным),, которое в первом классе сокращаем Р., но, начиная со второго класса, РОЗ.
Третье опорное слово всегда содержится в вопросе. В данной задаче третье опорное слово – ВСЕГО, которое в краткой записи задачи заменяется ФИГУРНОЙ СКОБКОЙ С ВОПРОСОМ ПОСЕРЕДИНЕ.
Потренируйся
Прочитай задачи и подчеркни УСЛОВИЕ – синей ручкой, ВОПРОС – зелёной ручкой. ОПОРНЫЕ СЛОВА – обведи в овал простым карандашом.
Здесь посмотри задачи для тренировки и скачай себе на компьютер.
Как записывать и решать простые задачи. Все типы задач. | ||
Все типы простых задач и способы записи условия задач | ||
КАК РАБОТАТЬ С ЗАДАЧНИКОМ
| ||
| ||
Статья «Формы составления краткой записи при решении текстовых задач»
Формы составления краткой записи при решении текстовых задач
Учитель начальных классов
МКОУ «Курская СШ» –
Якименко Е.А.
Одним из сложных вопросов преподавания математики является методика решения задач. В этом нас убеждают результаты анализа ошибок, допущенных в контрольных работах по математике, проблем, которые возникают во время выполнения домашних заданий.
Большие трудности у детей вызывает анализ задачи, а ведь именно здесь ключ к ее решению.
Нахождение пути решения задачи во многом определяется тем, сумеют ли учащиеся выделить величины, входящие в задачу, и правильно установить зависимости между ними. Этому в немалой степени способствует составление краткой записи в такой форме, чтобы появилась модель жизненной ситуации, описанной в задаче. Эта модель позволит упростить, отбросить несущественное и вскрыть связь между величинами.
Умелое руководство при составлении краткой записи, постоянное увеличение доли самостоятельности учащихся в этой работе должны привести к тому, что учащиеся в процессе решения задач, прежде чем бездумно складывать, умножать и т. д. имеющиеся числовые данные, нарисуют небольшую схему или чертеж задачи, что поможет им понять, осмыслить математическую сущность.
При составлении краткой записи к задаче следует руководствоваться положениями: 1. Краткая запись выполняется после ознакомления с содержанием задачи и служит важным средством поиска путей решения. Опираясь на нее, учащиеся под руководством учителя проводят разбор задачи;
2. Краткая запись должна быть лаконичной, четкой и наглядно отражать зависимости между величинами. Она может быть выполнена в различной форме: в форме таблицы, чертежа, рисунка, схемы и т. д.
3. Каждый новый вид краткой записи учащиеся выполняют под руководством учителя.
4. В зависимости от целей урока и степени сложности задачи записать ее кратко на доске может учитель или ученик под руководством учителя.
Опоры-перфокарты в обучении решению задач
Многие простые задачи содержат одну величину, значения которой связаны одним числовым равенством. Например:
1. «В детский сад привезли молоко в двух бидонах: в одном 32 л, в другом 30 л. Сколько всего литров молока привезли?»
Записать кратко эту простую задачу, можно было бы так:
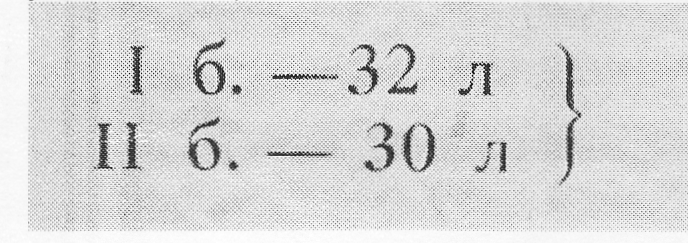
2. «В детский сад привезли 32 л молока. На обед израсходовали 40 л молока! Сколько литров молока осталось?»
Эту задачу можно записать в краткой форме следующим образом: Привезли — 32 л Израсходовали — 20 л Осталось — ?
Формирование умения записывать кратко простую задачу — необходимый элемент в обучении решению простых задач и подготовительный этап к ознакомлению с задачами в два действия. Для этой цели можно использовать опоры-таблицы, выполненные по принципу перфокарт. Каждая таблица представляет определенный вид задач: нахождение суммы или одного из слагаемых (рис. 1 и 2), нахождение остатка, уменьшаемого или вычитаемого (рис. 3), увеличение или уменьшение числа на несколько единиц (рис. 4), на разностное сравнение чисел (рис. 5).
Прорези удобны тем, что, прикрепив опору к доске, в прорезях можно записать недостающие числа, слово, знак «?» и получить краткую запись конкретной задачи. Использование данных опор приучает первоклассников правильно оформлять задачи (постоянно видят образец), дает возможность при работе у доски составлять краткую запись задачи (недостающее главное слово на первых порах записывает учитель, по возможности подбирая слово, состоящее из изученных букв), помогает учиться различать задачи по их существенным признакам. Наряду с демонстрационными таблицами удобно использовать такие же индивидуальные (особенно для шестилеток), что позволяет включить в работу всех учеников.
Опоры можно применять как перфокарты, делая записи на подложенном под таблицу листочке. Недостающее главное слово ученики пишут сокращенно или проговаривают.
Изложим подробнее методику работы с опорами — краткими записями в I классе начальной школы. Например, при ознакомлении с решением задач на увеличение (уменьшение) числа на несколько единиц опоры-таблицы (рис. 9 и 10) к ним вводятся после ознакомления с новым материалом как обобщение.
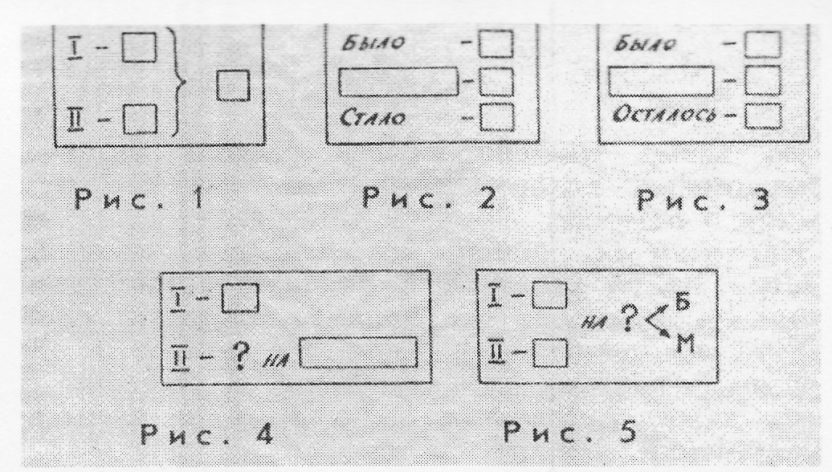
Работа над каждой задачей проводится в следующей последовательности: по рисунку составляется задача, уточняется, что значит на 3 больше (на 3 меньше), делается соответствующая запись: столько же да еще 3 (столько же, но без 3), обсуждается действие, которым решается задача. В ходе беседы с учащимися учитель оформляет краткую запись задачи, ее решение и ответ. Затем делаем обобщение по следующим вопросам: какие числа даны в задачах? Что спрашивалось в первой задаче? Ответьте на этот вопрос. Каков вопрос второй задачи? Дайте ответ. Итак, в обеих задачах данные числа одинаковы: 7 и 3 (опора на краткие записи), вопросы тоже одинаковы, но почему же различны ответы? (В первой задаче сказано «на 3 больше», а во второй — «на 3 меньше».) Слова «больше» и «меньше» для этих задач являются главными, от них зависит выбор действия для решения. Учитель размещает на доске таблицы так, как показано выше, и поясняет: «Решать задачи, в которых известное число нужно увеличить или уменьшить на несколько единиц, нам помогут эти опоры. На них показано, что одно число известно, а другое неизвестно (знак «?»), но про него сказано, на сколько оно больше или меньше известного».
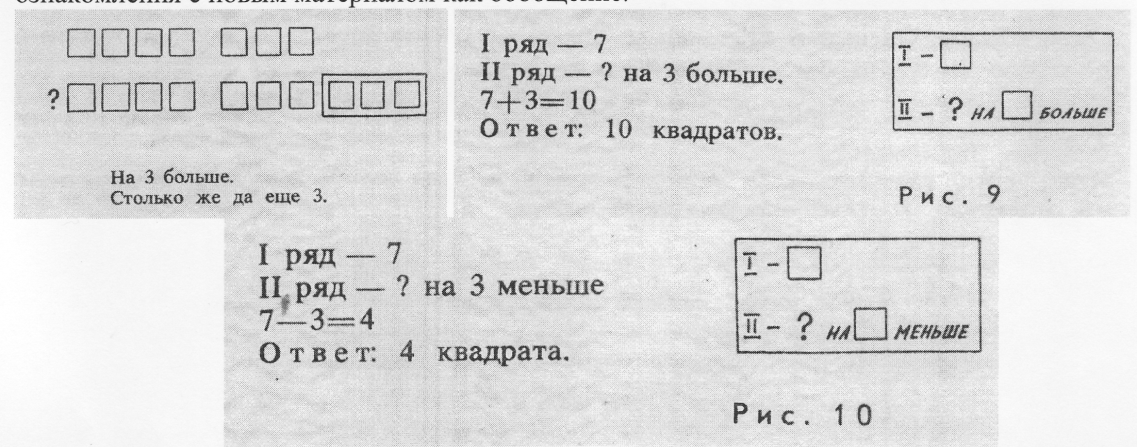
Для задач на увеличение (уменьшение) числа на несколько единиц нами используются сначала две различные таблицы: одна со словом «больше», другая со словом «меньше», тем самым подчеркивается различие между задачами. По мере овладения учениками решением таких задач вводится одна опора (рис. 4). В прорези вместе со вторым данным словом обозначается и отношение «больше», «меньше».
Активное и разнообразное использование опор-перфокарт при работе над простыми задачами способствует формированию в сознании ребенка наглядного образа задачи, решаемой одним действием, и готовит его к ознакомлению с задачами в два действия — составными.
Покажем методику использования опор при введении первой такой задачи. Учитель читает задачу: «В одном конверте 10 марок, а в другом — на 4 марки меньше. Сколько всего марок в двух конвертах?» — и одновременно ее иллюстрирует: прикрепляет к доске конверты с записанными на них данными числами (знак «?» на втором конверте ставится позже), повторяет вопрос задачи и пишет его на доске. Ученики по иллюстрации повторяют условие и вопрос. Им предлагается подобрать опору для краткой записи условия задачи. Дети выбирают таблицу для задачи на уменьшение числа на несколько единиц и вписывают в прорези данные числа. В последующей беседе они подводятся к пониманию необходимости выбора еще одной опоры и составления краткой записи данной задачи из двух опор:
— Какой вопрос задачи, которую записали кратко в выбранной опоре? (Сколько марок во втором конверте?)
— Какой вопрос в задаче, записанной на доске? (Сколько всего марок в двух конвертах?)
— Можно ли утверждать, что мы составили краткую запись данной задачи? (Нет, так как не подходит вопрос.)
— Как обозначить нужный нам вопрос? (Фигурной скобкой.)
— Нарисую фигурную скобку рядом с конвертами, поставлю цветным мелом знак «?» (рис. 13). Как на основе опоры, выбранной по условию задачи, составить ее краткую запись? Что еще нужно обозначить? (Записать вопрос задачи. Нарисовать на доске рядом с таблицей фигурную скобку и поставить знак «?».)
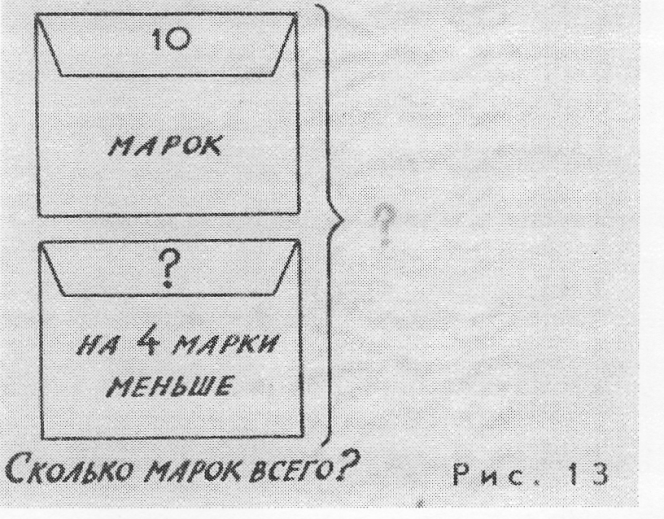
— Можно поступить и так. Но можно найти другой выход, ведь у нас есть еще опоры к задачам. Какая из них подойдет для обозначения вопроса данной задачи? (Ученики находят нужную таблицу. Она располагается
рядом с первой. Напротив фигурной скобки в прорезь
вставляется карточка со знаком«?», записанным цветным
фломастером.)
— Что должно быть известным в задаче, составленной по второй опоре? (Нужно задать первое и второе числа.)
— Значит, в условии должно быть оказано, сколько марок в первом конверте и сколько во втором. Такое ли условие в нашей задаче? (Нет, в ней дано число марок в первом конверте — 10, а во втором не дано.)
— Обозначим это во второй опоре. (Учитель вставляет карточки с числом 10 и знаком «?» в соответствующие прорези, рис. 14. Знак «?» он ставит и на втором конверте.)
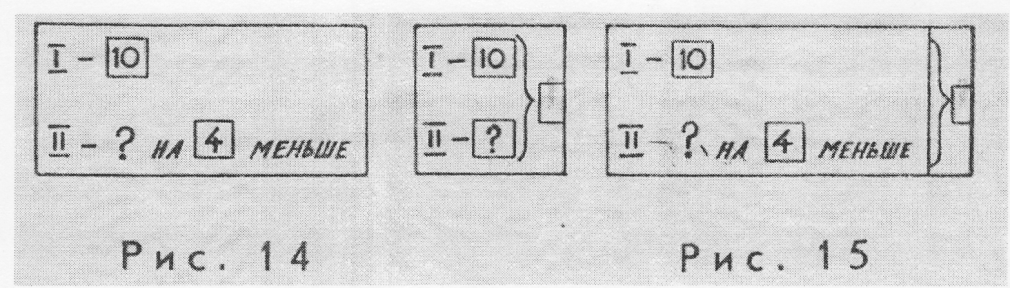
— Мы умеем решать задачи по первой и второй опорам. Для решения каждой из них выполняем одно действие. Это простые задачи. Записать кратко задачу о конвертах с марками с помощью одной только таблицы нам не удалось, потребовалось две таблицы: первая — для записи условия, а вторая — для вопроса. Следовательно, эта задача состоит из двух простых задач. Краткую запись для нее можно составить из двух опор, тогда будут записаны и условие, и вопрос. (Учитель показывает, как это делается: задвигает вторую таблицу под первую, оставляя фигурную скобку, рис. 15). Такая задача, составленная из двух простых задач, называется составной. Для ее краткой записи потребовалось две опоры, поэтому, выполнив по каждой опоре по одному действию, мы решим задачу двумя действиями. Опоры помогают и в поиске решения задачи. По краткой записи повторяются условие и вопрос. Уточняется, почему, кроме знака «?», обозначенного цветом — главного вопроса задачи, в ее краткой записи поставлен еще один такой знак? Таблица с фигурной скобкой отодвигается вправо. Рассуждая от искомого к данным, сначала работаем по этой опоре:
— Скажите главный вопрос задачи. (Сколько марок в двух конвертах?)
— Что нужно знать, чтобы ответить на него? (Количество марок и в первом, и во втором конвертах.)
— Все ли нам известно? (Нет, мы не знаем, сколько марок во втором конверте.)
— Поэтому мы не можем ответить на главный вопрос сразу, т. е. выполнив одно действие. Сначала нужно узнать, сколько марок во втором конверте, решить по первой опоре первую простую задачу. Можем ли ее решить? По каким данным? (В первом конверте 10 марок, а во втором на 4 марки меньше.)
— Какое действие выполним? (Вычитание, из 10 вычтем 4.)
— Запишем 10—4, но вычислять пока не будем, так как решение задачи еще не закончено. Перейдем ко второй опоре, чтобы решить вторую простую задачу. Мы узнали, что во втором конверте 10—4 марок (учитель ставит карточку с выражением 10—4 на знак «?» против цифры II), и известно также, что в первом конверте 10 марок. Можем ли мы теперь ответить на главный вопрос задачи? (Да.)
— Докажите. (Нужно сложить количество марок в первом и втором конвертах.)
— У нас записано 10—4, чтобы показать, что это действие выполнили первым, заключим 10—4 в скобки и прибавим 10. Вычислим, получим 16. Что означает это число? (16 марок в двух конвертах.)
Из двух таблиц снова составляется краткая запись составной задачи. Проводится обобщение: «Ответили ли мы на вопрос задачи? Сколько действий выполнили? Что нашли первым действием по первой опоре? Что нашли вторым по второй опоре? Почему мы не могли решить задачу одним действием?»
Таким образом, применение демонстрационных и индивидуальных опор-таблиц, изготовленных по принципу перфокарт, позволяет концентрировать внимание детей на существенных признаках задач нового вида. Опоры ассоциируются с определенным видом задач, что дает учащимся возможность увидеть в составной задаче несколько простых, облегчает понимание отличий между простой и составной задачами.
Использование чертежа при решении задач
Успешному решению задач способствует умение учащихся выделять величины, входящие в задачи, и правильно устанавливать зависимости между ними. Для этого необходимо уметь составлять краткую запись задачи так, чтобы она способствовала раскрытию связей между величинами.
Обнаружению связей между величинами способствует и схематический чертеж.
Приведем примеры двух задач разного вида с краткой записью и рисунком. 1. У девочки было 5 открыток. Она подарила 3 открытки. Сколько открыток осталось у девочки?
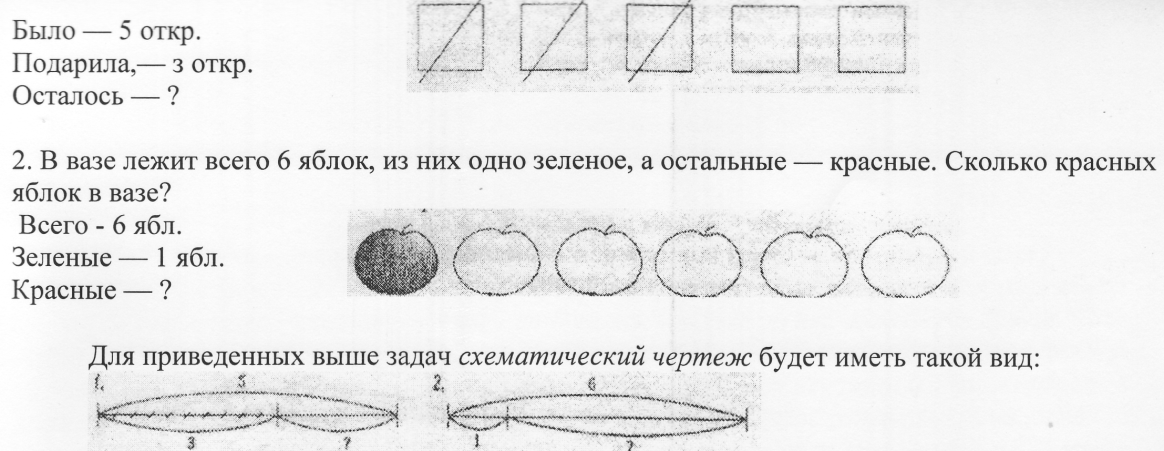
Такой чертеж отвечает следующим критериям: он исключает пересчет; может быть использован при решении задач со сколь угодно большими числовыми данными и задач, в которых числовые данные заменены буквами. Внешняя схожесть схем подчеркивает однотипность рассуждений при поиске решения задач: в каждой из них необходимо найти часть по известным целому и другой части.
Взяв за основу классификации простых задач не теоретическую основу выбора арифметического действия, а смысл понятий целое и часть, можно разбить все простые задачи, решаемые в I классе, на две группы;
1) задачи, решение которых сводится к нахождению целого по известным частям;
2) задачи на нахождение неизвестной части по известным целому и другой части.
Установим соответствие между задачами двух классификаций с помощью таблицы, составленной Смирновой С. И.:


Опыт показывает, что большинство учащихся понимает задание решить, задачу как необходимость ответить на вопрос и при возникающих трудностях подбирает ответ, затрудняясь объяснить, как он может быть найден. Поэтому задание «решить задачу» — это прежде всего необходимость обосновал» выбор арифметическою действия, которое нужно выполнить, чтобы ответить на вопрос задачи. При использовании чертежа учащиеся как правило, не испытывают затруднений при объяснении, так как за каждым словом стоит образ — отрезок а еще раньше — предметное действие. Объяснение же без опоры на такую наглядность требует достаточно высокого уровня развития у учащихся словесно-логического мышления, что не характерно для младших школьников,
Овладение описанной выше деятельностью позволит детям быть более активными участниками учебного процесса, самостоятельно справляться с решением целого ряда простых задач.
Работа над конкретной задачей может строиться по плану:
1. Чтение текста.
2. Изображение схематического рисунка.
После этого, опираясь на чертеж, проводится работа по тексту: Что известно в задаче? Покажите данные и искомые величины на чертеже. Что нужно найти?
После записи решения можно еще раз повторить задачу: Что нашли? Как нашли? Полезным является решение задач с недостающими или лишними данными, Например;
1. Из ведра отлили 3 л воды. Сколько воды было в ведре?
2. Миша прочитал всю книгу, в которой 16 страниц, за 2 дня, В первый день он прочитал 6 страниц, а во второй — 10 страниц. Сколько страниц в книге?
Заметим, что при решении задач на нахождение целого по известным частям полезно показать другой чертеж:

Использование такой схемы более удобно при. решении задачи: «Купили 10 пар лыж и столько же пар лыжных палок. Сколько пар лыж с палками купили?» Слова столько же указывают, что мы должны нарисовать равные отрезки, а это удобнее сделать, разместив их один под другим. Кроме того, последняя схема подготавливает учащихся к решению составных задач.
Опыт показывает, что дети без особых трудностей, естественно переходят к решению задач в два действия.

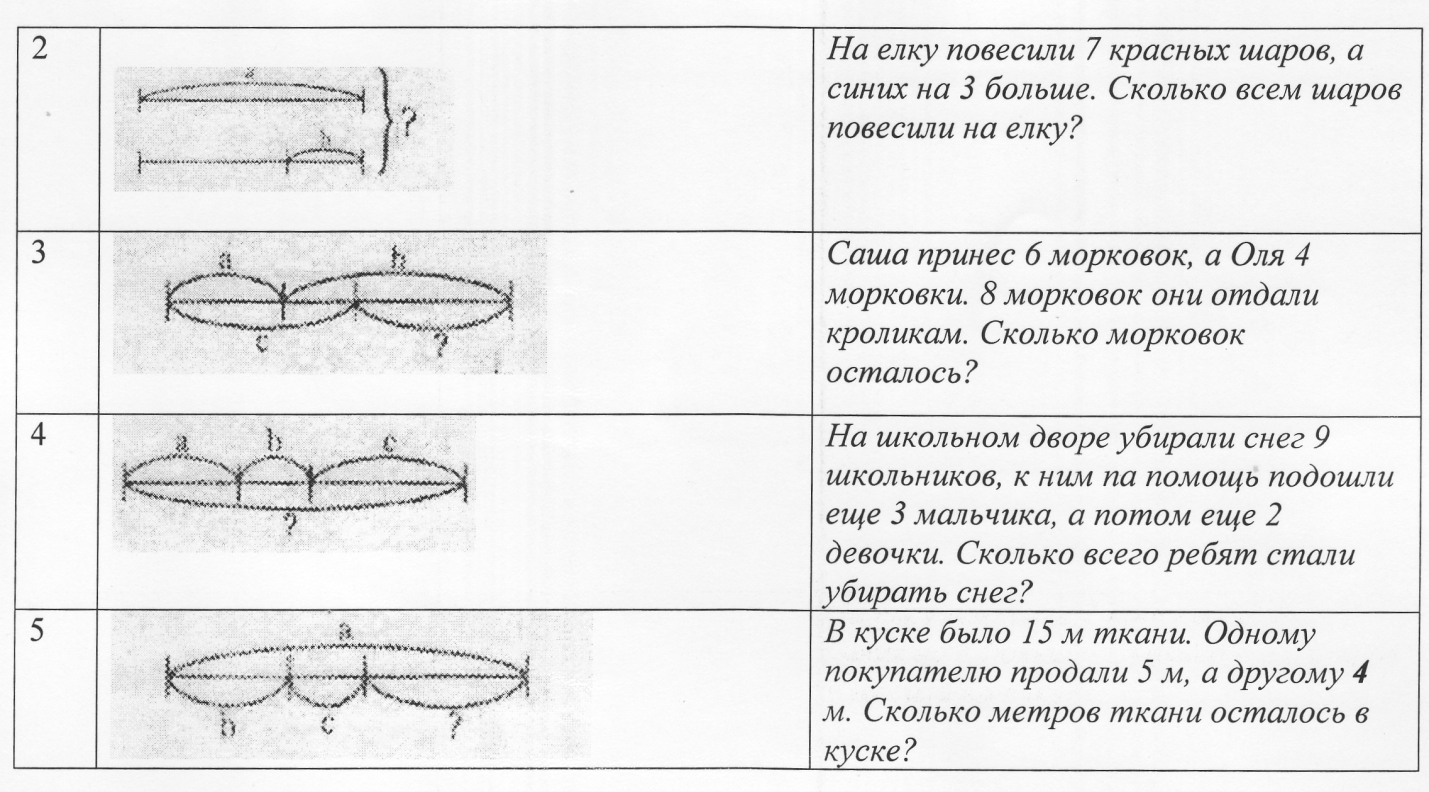
Решение задач из второй и четвертой групп похожи, так как обе простые задачи, входящие в их состав, — это задачи на нахождение целого по частям. Задачи из первой и третьей групп включают различные простые задачи: одна — на нахождение части, другая -целого по известным частям. Задачи пятой группы могут быть решены двумя способами, так как искомую величину можно рассматривать как часть величины а (тогда вторая часть — Ь + с) или как часть величины а — Ь {тогда вторая часть есть величина с). Особый интерес представляют задачи третьей группы: в зависимости от с искомая величина может быть найдена одним (при о а) или двумя {при с < а) способами.
Использование графических схем при решении задач
Продолжается поиск эффективных приёмов и методов при решении задач, которые помогут всем учащимся овладеть умениями решать задачи, позволит выделить опыт работы учителей-новаторов, рассмотреть рекомендации методистов по использованию графических схем для решения задач.
М.В. Богданович подчеркивал, что «схематическое изображение какого-нибудь вида задач не обязательно должно иметь единую форму. Стоит показывать разные формы записи одной и той же задачи». В процессе работы с графическими схемами учащиеся сами предлагают свои варианты графического изображения.
На основе схем, предложенных в методической литературе для простых задач, Г.Ф. Чистякова (Початкове навчання та виховання, № 10 (86), квггень 2006 р.) составила графические модели к составным задачам различных типов. (Здесь дано в сокращении).
класс
1.Задачи на нахождение суммы.

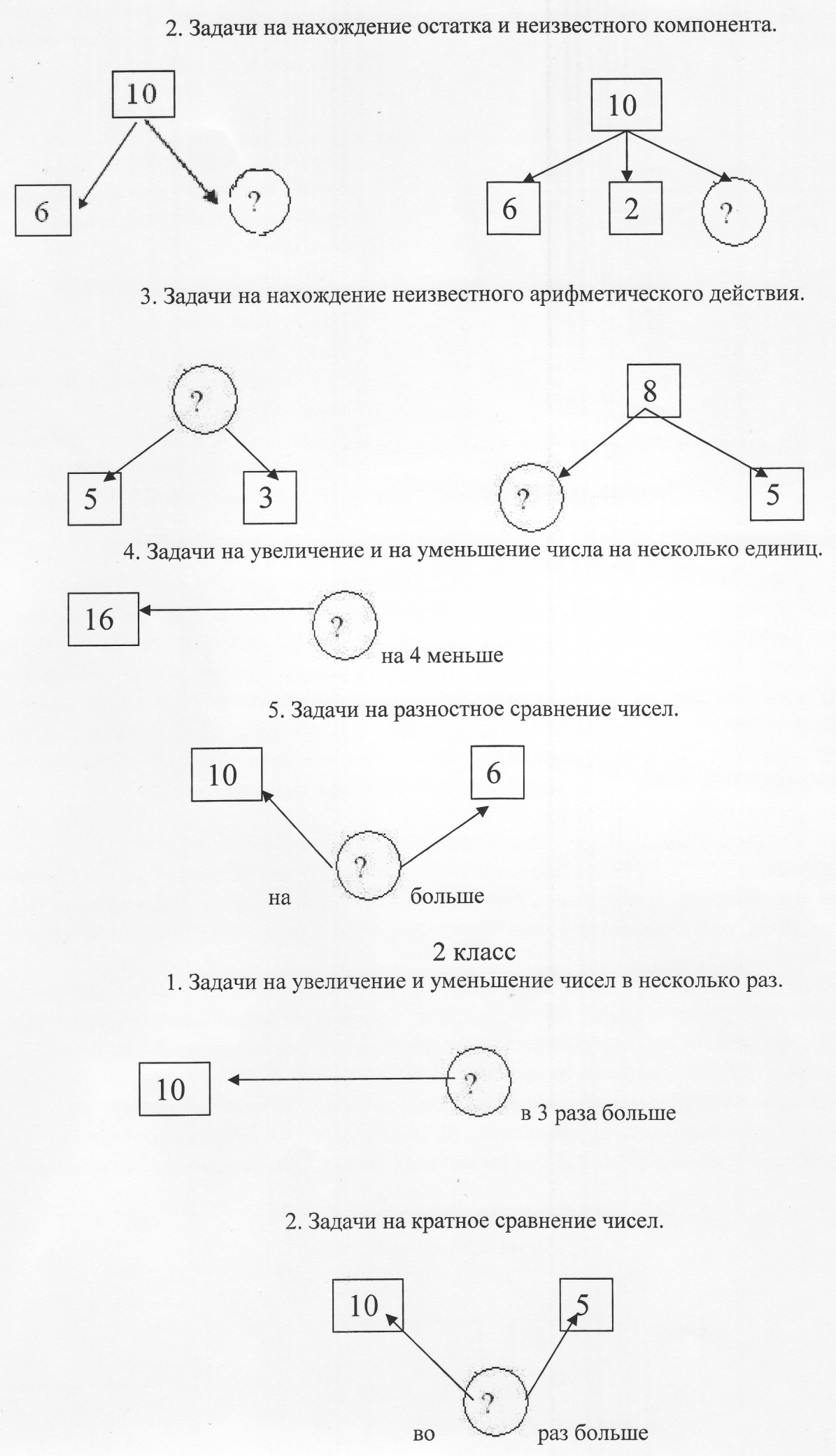
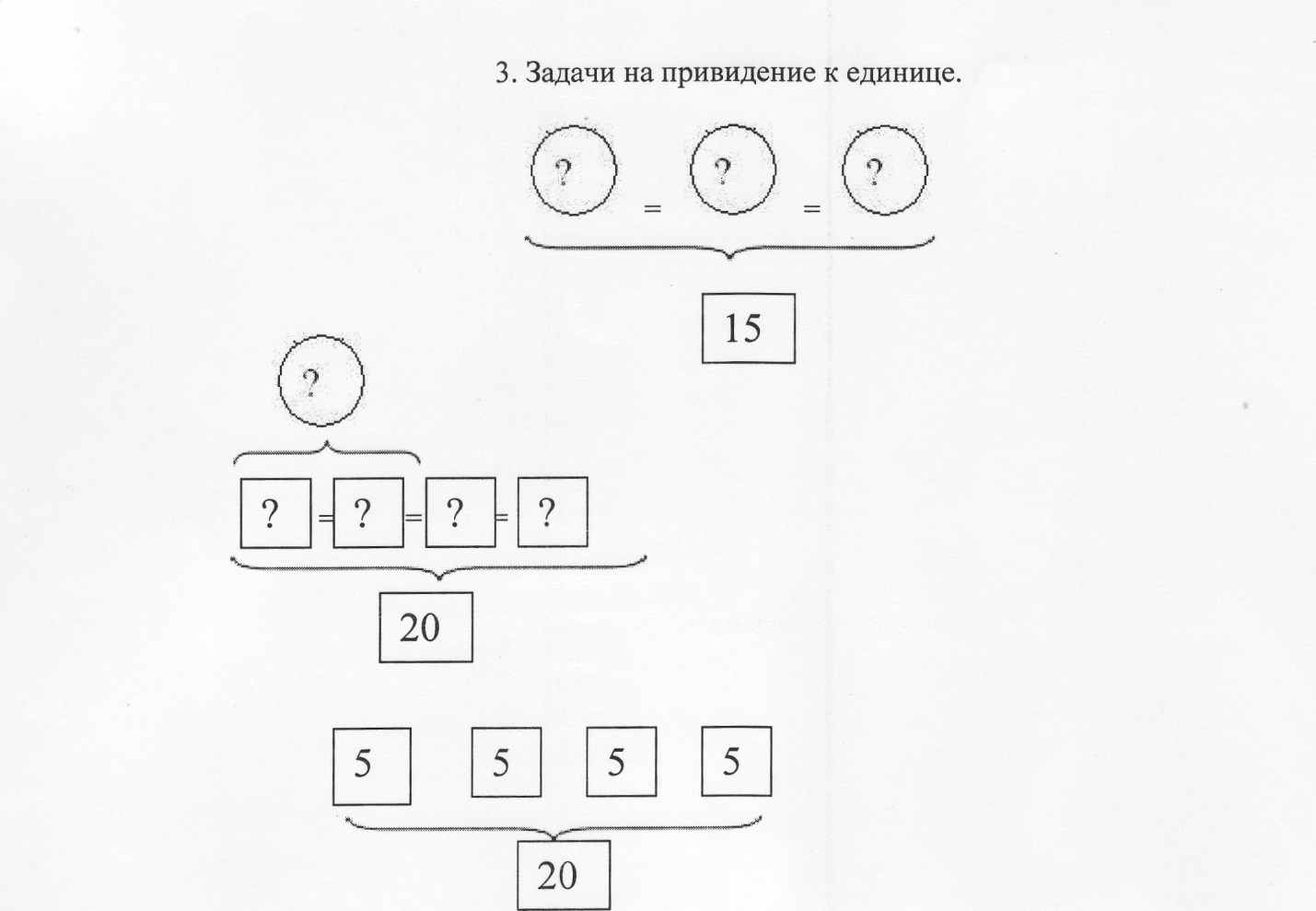
Итак, при специальной организации учебного процесса схематический чертеж, графические схемы могут стать для учащихся действенным средством поиска решения задачи. Кроме того, подробное обоснование учеником своих действий при построении схемы способствует развитию умения рассуждать, учит последовательно и аргументировано излагать свои мысли.
Литература
1. Ю.Никитина, И. Ковалевская. Решение текстовых задач способом моделирования. Початкова освита, № 44 (524), ноябрь 2009 р.
2.Г.Ф.Чистякова. Использование графических схем при решении задач по математике в начальной школе. Початкове навчання та виховання, № 10 (86), апрель 2006 р.
3. СИ. Смирнова. Использование чертежа при решении простых задач.
4. Н.Л. Гребенникова. Опоры-перфокарты в обучении решению задач.
Начальная школа, № 7-8, 1992 г
5. Л. В. Игнатова. Приемы установления зависимости между величинами в задачах. Начальная школа, №2, 1988 г.
Учебно-методический материал по математике (1 класс) на тему: Памятка по оформлению краткой записи к задачам
Слайд 1
Памятка по оформлению краткой записи к задачам 1-2 класс Выполнила: учитель начальных классов Арутюнян М. Р.Слайд 2
Содержание Простые задачи Нахождение суммы 1 2 3 Увеличение числа на несколько единиц 4 Уменьшение числа на несколько единиц 5 Нахождение неизвестного слагаемого 6 7 Нахождение остатка 8 Нахождение неизвестного вычитаемого 9 Нахождение неизвестного уменьшаемого 10 Разностное сравнение 11 12 Составные задачи Нахождение суммы 13 14 15 16 Нахождение остатка 17 18 Нахождение неизвестного слагаемого 19 20 Нахождение неизвестного вычитаемого 21 22 23 Нахождение третьего слагаемого 24 Нахождение неизвестного уменьшаемого 25 26 Разностное сравнение 27 28 29
Слайд 3
Аня вымыла 5 тарелок, а Миша вымыл 4 тарелки. Сколько всего тарелок вымыли дети? Аня – 5 т. ? т. Миша – 4 т. 5 + 4 = 9 (т.) Ответ: 9 тарелок вымыли дети. Задача №1
Слайд 4
На стоянке было 2 грузовика. Вечером приехало ещё 5 грузовиков Сколько всего грузовиков на стоянке? Было – 2 г. Приехало – 5 г. Стало – ? г. 2 + 5 = 7 (г.) Ответ: 7 грузовиков всего на стоянке. Задача №2
Слайд 5
На опушке леса росло 5 клёнов и 4 тополя, а сосен росло столько, сколько клёнов и тополей вместе. Сколько сосен росло на опушке леса? Клёнов – 5 д. Тополей – 4 д. Сосен – ? д., К. + Т. 5 + 4 = 9 (д.) Ответ: 9 сосен росло на опушке леса. Задача №3
Слайд 6
У Васи 7 марок, а у Егора на 3 марки больше. Сколько марок у Егора? Вася – 7 м. Егор – ? м., на 3 м. > 7 + 3 = 10 (м.) Ответ: 10 марок у Егора. Задача №4
Слайд 7
В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе? В I г. – 10 уч. Во II г. – ? уч., на 3 уч.
Слайд 8
У Ани было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Ани? Розовые – 5 р. 9 р. Белые – ? р. 9 – 5 = 4 (р.) Ответ: 4 белые розы были у Ани. Задача №6
Слайд 9
Дед Мазай вёз на своей лодке 5 зайцев. Он подобрал ещё несколько зайцев, и их стало 8. Сколько зайцев подобрал дед Мазай? Было – 5 з. Подобрал – ? з. Стало – 8 з. 8 – 5 = 3 (з.) Ответ: 3 зайца подобрал дед Мазай. Задача №7
Слайд 10
На проводах сидели 9 ворон. 5 ворон улетели. Сколько ворон осталось? Было – 9 в. Улетели – 5 в. Осталось – ? в. 9 – 5 = 4 (в.) Ответ: 4 вороны осталось. Задача № 8
Слайд 11
На кустике висело 7 ягод клубники. Когда несколько ягод созрело и упало, осталось 5 ягод. Сколько ягод созрело и упало? Было – 7 яг. Упало – ? яг. Осталось – 5 яг. 7 – 5 = 2 (яг.) Ответ: 2 ягоды созрело и упало. Задача № 9
Слайд 12
В зоопарке несколько медведей. Когда трёх медведей перевезли в другой зоопарк, осталось 6 медведей. Сколько медведей было в зоопарке первоначально? Было – ? м. Перевезли – 3 м. Осталось – 6 м. 3 + 6 = 9 (м.) Ответ: 9 медведей было в зоопарке первоначально. Задача № 10
Слайд 13
Один мальчик поймал 8 крабов, а другой 3 краба. На сколько крабов первый мальчик поймал больше второго? I м. – 8 к. на ? > II м. – 3 к. 8 – 3 = 5 (к.) Ответ: на 5 крабов первый мальчик поймал больше, чем второй. Задача № 11
Слайд 14
Один арбуз весит 5 кг, а другой 8 кг. На сколько килограммов один арбуз легче другого? I ар. – 5 кг на ?
Слайд 15
На пришкольном участке 6 берёз, а лип на 4 меньше. Сколько всего деревьев на пришкольном участке? Берёз – 6 д. ? д. Лип – ?д., на 4 д. Ответ: 8 деревьев всего на пришкольном участке . Задача № 13 1) 6 – 4 = 2 (д.) – лип 2) 6 + 2 = 8 (д.)
Слайд 16
В шкафу стоят 2 кастрюли, сковородок на 3 больше, а ваз столько, сколько кастрюль и сковородок вместе. Сколько ваз стоит в шкафу? Кастрюли – 2 шт. Сковородки – ? шт., на 3 шт. > Вазы – ? шт., К. + С. Ответ: 7 ваз стоит в шкафу . Задача № 14 1) 2 + 3 = 5 (шт.) – сковородок 2) 2 + 5 = 7 (шт.)
Слайд 17
У Тани 3 яблока, груш на 2 больше, чем яблок, а персиков на 4 меньше, чем груш. Сколько всего фруктов у Тани? Яблоки – 3 шт. Груши – ? шт., на 2 шт. > ? шт. Персики – ? шт., на 4 шт.
Слайд 18
Жёлтых – 17 к. Зелёных – ? к., на 6 к. В коробке 17 жёлтых кубиков, зелёных на 6 меньше, чем жёлтых, а красных на 12 больше, чем зелёных и жёлтых кубиков вместе. Сколько всего кубиков в коробке? Ответ: 68 кубиков всего в коробке . Задача № 16 1) 17 – 6 = 11 (к.) – зелёных 2) 17 + 11 = 28 (к.) – жёлтых и зелёных вместе 3) 28 + 12 = 40 (к.) – красных 4) 28 + 40 = 68 (к.)
Слайд 19
Было – 4 г. и 6 г. Израсходовали – 8 г. Осталось – ? г. Нашли 4 белых гриба и 6 подосиновиков. 8 грибов пошло на суп. Сколько грибов осталось? Ответ: 2 гриба осталось . Задача № 17 1) 4 + 6 = 10 (г.) – было 2) 10 – 8 = 2 (г.)
Слайд 20
Было – 23 р. Подарил – 6 р. и 4 р. Осталось – ? р. У Феди в аквариуме плавали 23 рыбки? Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди? Ответ: 13 рыбок осталось в аквариуме у Феди . Задача № 18 1) 6 + 4 = 10 (р.) – подарил 2) 23 – 10 = 13 (р.)
Слайд 21
Было – 22 п. и 13 п. Прилетело – ? п. Стало – 49 п. На поле сидело 22 воробья и 13 синичек. Когда прилетело ещё несколько птиц, их стало 49. Сколько птиц прилетело? Ответ: 14 птиц прилетело . Задача № 19 1) 22 + 13 = 35 (п.) – было 2) 49 – 35 = 14 (п.)
Слайд 22
Было – 6 к. Причалило – 3 к. и ? к. Стало – 19 к. У причала стояло 6 катеров. Утром причалило 3 катера и несколько катеров причалило вечером, и после этого у причала стало 19 катеров. Сколько катеров причалило вечером? Ответ: 10 катеров причалило вечером . Задача № 20 1) 19 – 6 = 13 (к.) – причалило всего 2) 13 – 3 = 10 (к.)
Слайд 23
Было – 7 б. и 3 б. Улетело –? б. Осталось – 5 б. Маша увидела 7 белых и 3 пёстрых бабочек. Когда несколько бабочек улетело, их осталось 5. Сколько бабочек улетело? Ответ: 5 бабочек улетело . Задача № 21 1) 7 + 3 = 10 (б.) – было 2) 10 – 5 = 5 (б.)
Слайд 24
Было – 20 в. Улетели – 10 в. и ? в. Осталось – 6 в. На аэродроме было 20 вертолётов. Утром улетело 10 вертолётов. Сколько вертолётов улетело днём, если к вечеру их осталось 6? Ответ: 4 вертолёта улетело днём . Задача № 22 1) 20 – 6 = 14 (в.) – улетели всего 2) 14 – 10 = 4 (в.)
Слайд 25
Было – 9 г. Завяли – ? г. Осталось – 2 г. и 3 г. В букете было 9 гвоздик. Когда несколько гвоздик завяли, остались 2 красные и 3 розовые гвоздики. Сколько гвоздик завяло? Ответ: 4 гвоздики завяло . Задача № 23 1) 2 + 3 = 5 (г.) – осталось 2) 9 – 5 = 4 (г.)
Слайд 26
В трёх классах на окнах стоят 35 горшков с цветками. В первом классе 11 горшков, во втором 13. Сколько горшков с цветками стоит в третьем классе? Ответ: 11 горшков с цветками стоят в третьем классе. Задача № 24 1)11 + 13 = 24(г.) – в I и II классах 2)35 – 24 = 11(г.) I к. – 11 г.. II к. – 13 г. 35 г. III к. – ? г.
Слайд 27
Бабушка испекла блины. Папа съел 15 блинов, мама 10. Сколько всего блинов испекла бабушка, если осталось 22 блина? Ответ: 47 блинов всего испекла бабушка. Задача № 25 1)15 + 10 = 25(б.) – съели 2)25 + 22 = 47 (б.) Было – ? б. Съели – 15 б. и 10 б. Осталось – 22 б.
Слайд 28
В пенале лежали карандаши. Когда туда положили ещё 3 простых и 7 цветных карандашей, их стало 22. Сколько карандашей лежало в пенале сначала? Ответ: 12 карандашей лежало в пенале сначала. Задача № 26 1)3 + 7 = 10 (к.) – положили 2)22 – 10 = 12 (к.) Было – ? к. Положили – 3 к. и 7 к. Стало – 22 к.
Слайд 29
В зале музея 18 картин. Из них 6 пейзажей, а остальные портреты. На сколько больше портретов, чем пейзажей? Ответ: на 6 портретов больше, чем пейзажей. Задача № 27 1) 18 – 6 = 12 (к.) – портреты 2)12 – 6 = 6 (к.) Пейзажи – 6 к. 18 к. на ? > Портреты – ? к.
Слайд 30
В саду 15 кустов малины, кустов крыжовника на 3 меньше, чем малины, а кустов смородины на 11 больше, чем малины. На сколько меньше кустов смородины, чем крыжовника и малины вместе? Ответ: на 1 куст меньше смородины, чем крыжовника и малины вместе. Задача № 28 1) 15 – 3 = 12 (к.) – крыжовника 2) 15 + 11 = 26 (к.) – смородины 3) 15 + 12 = 27 (к.) – малины и крыжовника вместе 4) 27 – 26 = 1 (к.) Малина – 15 к. Крыжовник – ? к., на 3 к.
Слайд 31
Над полянкой кружились 8 пчёл и 11 стрекоз. 15 из них сели на цветы. На сколько больше насекомых село на цветы, чем продолжало кружиться? Ответ: на 11 насекомых больше село на цветы, чем продолжало кружиться. Задача № 29 1) 8 + 11 = 19 (н.) – было 2) 19 – 15 = 4 (н.) – осталось 3) 15 – 4 = 11 (н.) Было – 8 н. и 11 н. Сели – 15 н. Осталось – ? н. на ? >
Слайд 32
http://files.vector-images.com/clipart/crab_mhk1.gif — краб http://files.vector-images.com/clipart/birch2.gif — берёза http://files.vector-images.com/clipart/vase_shlp1.gif — ваза http://files.vector-images.com/clipart/apples-lo-252.gif — яблоки http://i023.radikal.ru/0801/c2/2f07708f837c.jpg — — кубики http://files.vector-images.com/clipart/mushroom_shlp1.gif — гриб http://files.vector-images.com/clipart/aquarium2.gif — аквариум http://static.freepik.com/image/th/11-936.jpg — птица http://www.clipartov.net/images/mini/07/0000006490.jpg — катер http://files.vector-images.com/clipart/butterfly_shlp2.gif — бабочка http://files.vector-images.com/clipart/helicopter_vsl5.gif — вертолёт http://files.vector-images.com/clipart/carnation_oa1.gif — гвоздика http://files.vector-images.com/clipart/rose_oa6.gif — роза Используемые источники Узорова О. В. Нефедова Е. А. 2518 задач по математике 1 -4 классы Издательство «Астрель», 2009 http://files.vector-images.com/clipart/flower_shlp2.gif — цветок в горшке
Слайд 33
http://files.vector-images.com/clipart/mardigras_001.gif — блины http://files.vector-images.com/clipart/pencil_shlp2.gif — карандаш http://cartoonclipartfree.com/Cliparts_Free/Gegenstaende_Free/Cartoon-Clipart-Free-78.gif — картина http://img-fotki.yandex.ru/get/5813/119528728.d09/0_a241c_e903c84b_XL — куст малины http://files.vector-images.com/clipart/insect_mhl2.gif — стрекоза http://files.vector-images.com/clipart/kitchen_prg28.gif — тарелки http://files.vector-images.com/clipart/hare1.gif — заяц http://files.vector-images.com/clipart/schoolboy_gk12.gif — ученик http://files.vector-images.com/clipart/truck6.gif — грузовик http://files.vector-images.com/clipart/pine1.gif — сосна http://www.vectory.ru/products_pictures/vorona00712.gif — ворона http://img.cliparto.com/pic/s/187502/3202247-postage-stamp.jpg — марка http://files.vector-images.com/clipart/strawberry_hr1.gif — клубника http://4-8class-math-forum.ru/i/p/6-1-6-b522.gif — 1 слайд http://files.vector-images.com/clipart/bear8.gif — медведь http://files.vector-images.com/clipart/watermelon_okh2.gif — арбуз
Презентация к уроку по математике (1 класс) на тему: Памятка по оформлению краткой записи к задачам 1 класса
Слайд 1
Памятка по оформлению краткой записи к задачам 1-2 класс Застенкина-Клименко Ольга Александровна учитель начальных классов ОШ №63 г. ДонецкаСлайд 2
Содержание Простые задачи Нахождение суммы 1 2 3 Увеличение числа на несколько единиц 4 Уменьшение числа на несколько единиц 5 Нахождение неизвестного слагаемого 6 7 Нахождение остатка 8 Нахождение неизвестного вычитаемого 9 Нахождение неизвестного уменьшаемого 10 Разностное сравнение 11 12 Составные задачи Нахождение суммы 13 14 15 16 Нахождение остатка 17 18 Нахождение неизвестного слагаемого 19 20 Нахождение неизвестного вычитаемого 21 22 23 Нахождение третьего слагаемого 24 Нахождение неизвестного уменьшаемого 25 26 Разностное сравнение 27 28 29
Слайд 3
Задача 1 Нахождение суммы Ася вымыла 5 тарелок, а Маша вымыла 4 тарелки. Сколько всего тарелок вымыли дети? Ася – 5 т. ? Т. Маша – 4 т. Решение 5 + 4 = 9 (т.) Ответ: 9 тарелок вымыли дети.
Слайд 4
Задача 2 Нахождение суммы На стоянке было 2 машины. Вечером приехало ещё 5 машин. Сколько всего машин на стоянке? Было – 2 м. Приехало – 5 м. Стало – ? м. Решение 2 + 5 = 7 (м.) Ответ: 7 машин всего на стоянке.
Слайд 5
Задача 3 Нахождение суммы На опушке леса росло 5 клёнов и 4 тополя, а сосен росло столько, сколько клёнов и тополей вместе. Сколько сосен росло на опушке леса? Клёнов – 5 д. Тополей – 4 д. Сосен – ? д., К. + Т. Решение 5 + 4 = 9 (д.) Ответ: 9 сосен росло на опушке леса.
Слайд 6
Задача 4 Увеличение числа на несколько единиц У Васи 7 марок, а у Егора на 3 марки больше. Сколько марок у Егора? Вася – 7 м. Егор – ? м., на 3 м. > Решение 7 + 3 = 10 (м.) Ответ: 10 марок у Егора.
Слайд 7
Задача 5 Уменьшение числа на несколько единиц В первой группе 10 учеников, а во второй на 3 ученика меньше. Сколько учеников во второй группе? В I г. – 10 уч . Во II г. – ? уч ., на 3 уч .
Слайд 8
Задача 6 Нахождение неизвестного слагаемого У Дины было 9 роз. 5 розовых, остальные белые. Сколько белых роз было у Дины ? Розовые – 5 р. 9 р. Белые – ? р. Решение 9 – 5 = 4 (р.) Ответ: 4 белые розы были у Дины .
Слайд 9
Задача 7 Нахождение неизвестного слагаемого Дед Мазай вёз на своей лодке 5 зайцев. Он подобрал ещё несколько зайцев, и их стало 8. Сколько зайцев подобрал дед Мазай ? Было – 5 з . Подобрал – ? з . Стало – 8 з . Решение 8 – 5 = 3 ( з .) Ответ: 3 зайца подобрал дед Мазай .
Слайд 10
Задача 8 Нахождение остатка На проводах сидели 9 ворон. 5 ворон улетели. Сколько ворон осталось? Было – 9 в. Улетели – 5 в. Осталось – ? в. Решение 9 – 5 = 4 (в.) Ответ: 4 вороны осталось.
Слайд 11
Задача 9 Нахождение неизвестного вычитаемого На кустике висело 7 ягод клубники. Когда несколько ягод созрело и упало, осталось 5 ягод. Сколько ягод созрело и упало? Было – 7 яг . Упало – ? яг . Осталось – 5 яг . Решение 7 – 5 = 2 ( яг .) Ответ: 2 ягоды созрело и упало.
Слайд 12
Задача 10 Нахождение неизвестного уменьшаемого В зоопарке несколько медведей. Когда трёх медведей перевезли в другой зоопарк, осталось 6 медведей. Сколько медведей было в зоопарке первоначально? Было – ? м. Перевезли – 3 м. Осталось – 6 м. Решение 3 + 6 = 9 (м.) Ответ: 9 медведей было в зоопарке первоначально.
Слайд 13
Задача 11 Разностное сравнение Один мальчик поймал 8 крабов, а другой 3 краба. На сколько крабов первый мальчик поймал больше второго? I м. – 8 к. II м. – 3 к.
Слайд 14
Задача 12 Разностное сравнение Один арбуз весит 5 кг, а другой 8 кг. На сколько килограммов один арбуз легче другого? I ар. – 5 кг
Слайд 15
Задача 13 Нахождение суммы На пришкольном участке 6 берёз, а лип на 4 меньше . Сколько всего деревьев на пришкольном участке? Берёз – 6 д. ? д. Лип – ?д., на 4 д.
Слайд 16
Задача 14 Нахождение суммы В шкафу стоят 2 кастрюли, сковородок на 3 больше , а ваз столько, сколько кастрюль и сковородок вместе. Сколько ваз стоит в шкафу? Кастрюли – 2 шт. Сковородки – ? шт., на 3 шт. > Вазы – ? шт., К. + С. Решение 2 + 3 = 5 (шт.) – сковородок. 2 + 5 = 7 (шт.) Ответ: 7 ваз стоит в шкафу.
Слайд 17
Задача 15 Нахождение суммы У Тани 3 яблока, груш на 2 больше , чем яблок, а персиков на 4 меньше , чем груш. Сколько всего фруктов у Тани? Яблоки – 3 шт. Груши – ? шт., на 2 шт. > ? шт. Персики – ? шт., на 4 шт.
Слайд 18
Задача 16 Нахождение суммы В коробке 17 жёлтых кубиков, зелёных на 6 меньше , чем жёлтых, а красных на 12 больше , чем зелёных и жёлтых кубиков вместе . Сколько всего кубиков в коробке? Жёлтых – 17 к. ? К. Зелёных – ? к., на 6 к. Решение 17 – 6 = 11 (к.) – зелёных. 17 + 11 = 28 (к.) – жёлтых и зелёных вместе. 28 + 12 = 40 (к.) – красных. 28 + 40 = 68 (к.) Ответ: 68 кубиков всего в коробке.
Слайд 19
Задача 17 Нахождение остатка Нашли 4 белых гриба и 6 подосиновиков. 8 грибов пошло на суп. Сколько грибов осталось? Было – 4 г. и 6 г. Израсходовали – 8 г. Осталось – ? г. Решение 4 + 6 = 10 (г.) – было. 10 – 8 = 2 (г.) Ответ: 2 гриба осталось.
Слайд 20
Задача 18 Нахождение остатка У Феди в аквариуме плавали 23 рыбки. Мальчик подарил 6 рыбок Ване и 4 рыбки Максиму. Сколько рыбок осталось в аквариуме у Феди? Было – 23 р. Подарил – 6 р. и 4 р. Осталось – ? р. Решение 6 + 4 = 10 (р.) – подарил. 23 – 10 = 13 (р.) Ответ: 13 рыбок осталось в аквариуме у Феди.
Слайд 21
Задача 19 Нахождение неизвестного слагаемого На поле сидело 22 воробья и 13 синичек. Когда прилетело ещё несколько птиц, их стало 49. Сколько птиц прилетело? Было – 22 п. и 13 п. Прилетело – ? п. Стало – 49 п. Решение 22 + 13 = 35 (п.) – было. 49 – 35 = 14 (п.) Ответ: 14 птиц прилетело.
Слайд 22
Задача 20 Нахождение неизвестного слагаемого У причала стояло 6 катеров. Утром причалило 3 катера и несколько катеров причалило вечером, и после этого у причала стало 19 катеров. Сколько катеров причалило вечером? Было – 6 к. Причалило – 3 к. и ? к. Стало – 19 к. Решение 19 – 6 = 13 (к.) – причалило всего . 13 – 3 = 10 (к.) Ответ: 10 катеров причалило вечером.
Слайд 23
Задача 21 Нахождение неизвестного вычитаемого Маша увидела 7 белых и 3 пёстрых бабочек. Когда несколько бабочек улетело, их осталось 5. Сколько бабочек улетело? Было – 7 б. и 3 б. Улетело –? б. Осталось – 5 б. Решение 7 + 3 = 10 (б.) – было. 10 – 5 = 5 (б.) Ответ: 5 бабочек улетело.
Слайд 24
Задача 22 Нахождение неизвестного вычитаемого На аэродроме было 20 вертолётов. Утром улетело 10 вертолётов. Сколько вертолётов улетело днём , если к вечеру их осталось 6? Было – 20 в. Улетели – 10 в. и ? в. Осталось – 6 в. Решение 20 – 6 = 14 (в.) – улетели всего. 14 – 10 = 4 (в.) Ответ: 4 вертолёта улетело днём.
Слайд 25
Задача 23 Нахождение неизвестного вычитаемого В букете было 9 гвоздик. Когда несколько гвоздик завяли, остались 2 красные и 3 розовые гвоздики. Сколько гвоздик завяло? Было – 9 г. Завяли – ? г. Осталось – 2 г. и 3 г. Решение 2 + 3 = 5 (г.) – осталось. 9 – 5 = 4 (г.) Ответ: 4 гвоздики завяло.
Слайд 26
Задача 24 Нахождение третьего слагаемого В трёх классах на окнах стоят 35 горшков с цветками. В первом классе 11 горшков, во втором 13. Сколько горшков с цветками стоит в третьем классе? I к. – 11 г. II к. – 13 г. 35 г. III к. – ? г. Решение 1)11 + 13 = 24(г.) – в I и II классах. 2)35 – 24 = 11(г.) Ответ: 11 горшков с цветками стоят в третьем классе.
Слайд 27
Задача 25 Нахождение неизвестного уменьшаемого Бабушка испекла блины. Папа съел 15 блинов, мама 10. Сколько всего блинов испекла бабушка , если осталось 22 блина? Было – ? б. Съели – 15 б. и 10 б. Осталось – 22 б. Решение 1)15 + 10 = 25(б.) – съели. 2)25 + 22 = 47 (б.) Ответ: 47 блинов всего испекла бабушка.
Слайд 28
Задача 26 Нахождение неизвестного уменьшаемого В пенале лежали карандаши. Когда туда положили ещё 3 простых и 7 цветных карандашей, их стало 22. Сколько карандашей лежало в пенале сначала? Было – ? к. Положили – 3 к. и 7 к. Стало – 22 к. Решение 1)3 + 7 = 10 (к.) – положили. 2)22 – 10 = 12 (к.) Ответ: 12 карандашей лежало в пенале сначала.
Слайд 29
Задача 27 Разностное сравнение В зале музея 18 картин. Из них 6 пейзажей, а остальные портреты. На сколько больше портретов, чем пейзажей? Пейзажи – 6 к. Портреты – ? к.
Слайд 30
Задача 28 Разностное сравнение В саду 15 кустов малины, кустов крыжовника на 3 меньше, чем малины, а кустов смородины на 11 больше, чем малины. На сколько меньше кустов смородины, чем крыжовника и малины вместе? Малина – 15 к.
Слайд 31
Задача 29 Разностное сравнение Над полянкой кружились 8 пчёл и 11 стрекоз. 15 из них сели на цветы. На сколько больше насекомых село на цветы, чем продолжало кружиться? Было – 8 н. и 11 н. Сели – 15 н. Осталось – ? н.
Учебно-методическое пособие по математике (3 класс) на тему: Оформление задач в начальной школе
24 туриста разбили лагерь и поселились в палатках. Сколько палаток оказалось в лагере, если в каждой палатке было по 3 туриста?
Задача.
24 туриста – ? пал.
3 туриста – 1 пал.
Решение:
24 : 3 = 8 (п.)
Ответ: в лагере было 8 палаток.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
В пруду плавают 7 уток, у каждой 5 утят. Сколько всего птиц плавает в пруду?
Задача. Задача.
1 утка – 5 утят. или Утки – 7 пт.
7 уток – ? утят. Утята – ? пт., по 5 пт. 7 раз. ? пт.
Всего – ? птиц.
Решение:
1) 5 ∙ 7 = 35 (пт.) – утят.
2) 35 + 7 = 42 (пт.) – всего.
35
или 5 ∙ 7 + 7 = 42 (пт.)
Ответ: в пруду плавает 42 птицы.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
В семи клетках разместили поровну 42 хомячка. Сколько хомячков оказалось в трёх клетках; в пяти клетках?
Задача.
В 7 кл. – 42 хом.
В 3 кл. – ? хом.
В 5 кл. – ? хом.
Решение: 6
1) 42 : 7 = 6(хом.) – в 1 клетке. или 1) 42 : 7 ∙ 3 = 18 (хом.) – в 3-х клетках.
2) 6 ∙ 3 = 18 (хом.) – в 3-х клетках. 2) 6 ∙ 5 = 30 (хом.) – в 5-и клетках.
3) 6 ∙ 5 = 30 (хом.) – в 5-и клетках.
Ответ: в 3-х клетках 18 хомяков; в 5-и клетках 30 хомяков.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
На стройке работали 8 строительных бригад по 10 человек в каждой. Сколько всего строителей трудились на стройке?
Задача.
1 бригада – 10 ч.
8 бригад – ? ч.
Решение:
10 ∙ 8 = 80(ч.)
Ответ: 80 строителей.
На столе лежала стопка тетрадей. Учитель отдал 8 ученикам по 7 тетрадей. После этого в стопке осталось 18 тетрадей. Сколько тетрадей было в стопке сначала?
Задача.
Было – ? тетр.
Отдал – ? тетр., по 7 тетр. 8 уч.
Осталось – 18 тетр.
Решение: 1
- 7 ∙ 8 = 56(тетр.) – отдал. 2) +56
18
56 74(тетр.) – было.
или 7 ∙ 8 + 18 = 74(тетр.)
Ответ: в стопке было 74 тетради.
___________________________________________________________________________________________________________________________
В 9 клетках сидели кролики, по 4 кролика в каждой клетке. 14 кроликов были белыми, остальные – чёрными. Сколько кроликов было чёрного цвета?
Задача.
Всего – ? кр., по 4 кр. в 9 кл. или Белые – 14 кр.
Белые – 14 кр. Чёрные – ? кр. ? кр., 9 кл. по 4 кр.
Чёрные – ? кр.
Решение: 1
1) 9 ∙ 4 = 36(кр.) – всего.
2) 36 – 14 = 22 (кр.) – чёрного цвета
36
или 9 ∙ 4 – 14 = 22(кр.)
Ответ: 22 кролика были чёрного цвета.
___________________________________________________________________________________________________________________________
В одном рулоне 42 м ткани, в другом – 21 м. На пошив комплекта постельного белья расходуется 7 м ткани. Сколько комплектов белья получится из всей ткани?
В I рул. – 42 м.
Во II рул. – 21 м. ? м – ? компл.
На 1 комплект – 7 м.
Решение:
I способ 63
1) 42 + 21 = 63 (м) – всего. или (42 + 21) : 7 = 9 (компл.)
2) 63 : 7 = 9 (компл.) – всего.
II способ 6 3
1) 42 : 7 = 6 (компл.) – из I рулона. или 42 : 7 + 21 : 3 = 9 (компл.)
2) 21 : 7 = 3 (компл.) – из II рулона.
3) 6 + 3 = 9 (компл.) – всего.
Ответ: из всей ткани получится 9 комплектов белья.